在计算机中实现三角函数的硬件解算方法
,,
(中船重工716研究所,江苏 连云港 222006)
在计算机中实现三角函数的硬件解算方法
袁岐川,龙玮洁,李建峰
(中船重工716研究所,江苏连云港222006)
针对目标跟踪中大量存在的三角函数运算,提出在火控计算机中建立三角函数解算单元,采用硬件实现三角函数解算的设想;而三角函数解算单元是一种可以完成正弦函数解算功能的函数芯片;它的设计核心是以角度值为地址,通过硬件查表计算,可对0到90度的正弦函数值进行查表;查表精度可设计到0.001°,最大查表时间即为函数值的解算时间;余弦查表计算是采用正弦同一芯片,可以根据相位差90度的关系进行查表;实践表明三角函数的硬件解算速度快,精度高,可以替代通常方法的函数解算;因此,如果在火控系统中,设计一个地址译码器电路,就可建立多个三角函数芯片解算单元,通过计算机数据指令,实现对多个三角函数值的并行计算,从而提高系统对多个目标的快速跟踪处理能力。
三角函数; 正弦算法; 芯片设计; 火控计算机
0 引言
火控计算机中如何加快三角函数的解算是跟踪处理大批目标的关键,建立三角函数解算单元,是实现三角函数硬件解算的最简单方法,它不同于火控计算机中为解决三角函数运算所采用的以DSP芯片为主的函数处理系统,这里所说的三角函数解算单元是一个具有独立功能的芯片,使用时只要给出函数值的地址,计算机无需参与函数的解算过程,芯片就能独立完成函数的解算任务,这是其它方法处理函数无法比的。创建硬件解算三角函数的思想,源自采用软件查表计算正弦sin(ωτ)和余弦cos(ωτ)函数的方法,它能显著提高三角函数的解算过程。在软件查表过程中,把函数值由小到大按顺序排列,根据函数值设计相应的地址,当计算某一函数值时,只要计算出函数值的地址就可获得其函数值,这是软件查表解算三角函数的方法。如果将软件查表实现三角函数的解算变为硬件查表实现,无疑将极大提高三角函数的解算速度,这就需要建立独立的三角函数解算芯片,幸运的是我们在工作中对三角函数解算的硬件实现,找到了简单实现的方法。
关于三角函数的硬件解算有没有现成的芯片,在学术层面上还没有见到报道,国外有可能限于军事性质已有,但不便公开。因此,我们研究三角函数硬件解算意义重大,越快越好。
我们知道在火控系统跟踪中,每一个跟踪目标都有大量的正弦、余弦函数运算,而函数运算在计算机中是采用泰勒级数方法求取的,极其费时,将函数的软件查表法通过硬件查表实现,从而取代目标运动参数中函数的解算,这是我们的目的。
1 三角函数解算单元的建立
1.1 芯片功能
要求三角函数解算单元芯片,只需给出函数值的地址,芯片就能自动获取该角度的函数值来。芯片完成操作,只用两条指令,写指令负责将角度值送到芯片端口去,然后芯片进行函数值的查表计算,再由读指令负责将转换完的函数值读取到计算机的累加器A中。函数的地址,由计算机根据所求角度计算。可对0到90度的自由变量进行正弦函数求解,查表精度为0.001°。如果精度要求高,也可设置的再高一些。
1.2 芯片原理
具有三角函数解算的芯片由EPROM和地址译码器组成,EPROM可写入0°到90°的正弦数据表,地址译码器负责函数值地址单元的选择。正弦数据表是利用计算机程序求出0到90度,步进间隔0.001°的90 000个正弦函数值,再将每一步的函数值乘以2的16次方(字长16位)所获得的二进制数,按顺序由小到大排列成的数据表。函数值在EPROM中的地址是以角度值乘以1 000而设计的,因此,每0.001°存放一个单元(字长为十六位),一个单元只存放一个二进制表示的函数值。这样0度到90度共占90 000个单元。所以,0度的函数值0000H在地址0H, 90度的函数值FFFFH的地址在90000,化为十六进制15F90H。见表1。

表1 EPROM中数据排放
芯片中的EPROM设计,如图1所示,存储器芯片内部有128 K个16位的存储单元,即存储容量为128 K×16位,有17根地址线,16根数据线,读/写控制线,片选线等。

图1 正弦函数芯片
每一个存储器芯片内部的存储单元都有2个地址,一个是芯片内部地址,一个是系统地址。内部地址是与外部连线无关的,每一个芯片内部地址范围都是从0000H~20000H。而系统地址取决于外部连线芯片中的译码器设计用17位地址线通过内部译码器选择存储单元。地址范围在00000H~20000H,实际使用范围是0000H~15F90H。
1.3 函数值的查表方法
将所求的正弦函数的自变量乘以1 000,就是该函数自变量的函数值的地址,由于每个函数值占一个单元,字长十六位,芯片的地址范围00000~15F90。
例如求取30°的函数值,先计算自变量30°的地址,方法是:把30乘以1 000,等于30 000,化为十六进制:7530H,即自变量30度的EPROMDE 的地址。通过写指令将地址7530H送到芯片端口,芯片就可根据地址获取7530H中的内容:8000H,即30°的函数值。然后,再由读指令读取芯片中的函数值到累加器A中。
1.4 三角函数单元芯片的验证
为了验证三角函数单元芯片中数据的正确性,我们将芯片中的数据读出,以正弦曲线表示。为此,我们从芯片中取数据,设计正弦周期长20秒,每间隔2.5毫秒取一个点,共取8 000个点,绘制一条正弦曲线图。由图的运动轨迹看以芯片中的数据做出的曲线符合正弦规律,数据在4个象限的曲线非常平滑,表明EPROM中的数据是正确的,正弦查表计算是可行的。这里给出的正弦曲线只是设计的一种情况,其它情况也可得到验证。需要说明的是,正弦芯片中数据的逐点验证,需要图形较大不便在论文中表示。

图2 根据正弦芯片中的数据所作的正弦曲线
1.5 硬件查表计算的速度比较
快速算法(软件查表法)在摇摆信号发生器中得到应用,对于三角函数的正弦芯片设计,人们想知道它的速度如何,为此,我们通过计算机编程实验,列出常用的正弦函数调用法与快速算法和硬件查表法三着差异。表格中的数据,说明它们之间的速度关系:
这是在不限定机型条件下的获取的数据。可以说明,无论什么条件下,硬件查表速度最快。

表3 3种算法比较
有关正弦函数芯片的设计,完全可以依据函数的快速算法来实现。我们把单片机的功能划分为相位累加器,相位寄存器,加法器,地址寄存器、比较器、控制器等几个部分,加上存储器,相关的集成电路制造商即可根据功能进行设计和制造。有了这样功能的芯片,函数解算时,计算机只需给芯片一个输入值,芯片就可以在十几个纳秒内,给出函数值。如果把这个函数芯片,应用到火控计算机中的公式解算,那么,公式中频繁的正弦余弦函数运算被函数芯片取代,计算机就会节省到大量的时间,火控计算机就有充分的时间对几百个运动目标实现跟踪和解算。
2 导致火控系统采用函数芯片重建
有了三角函数的快速解算方法,火控系统中关于函数的运算就应重新设计。把大量的sin(β),cos(ε)正弦、余弦函数运算从计算机中分离出来,建立以正弦三角函数单元为计算单元的函数处理系统。这里,余弦的算法,无需另外设计,由于它们相位相差是90度,正弦数据表的反向就是是余弦,即余弦的0°值是正弦的90°值,正弦余弦可以合用一种芯片,取值方法是:一个由0到90°,而另一个则由90到0°。
怎样重建,应该根据跟踪系统的要求,在系统中设计合理的三角函数解算单元阵列。
2.1 跟踪系统要求
目前,发达国家的火控处理系统可以同时跟踪处理400多个目标,我们应该以这个为目标设计我们的目标跟踪处理系统。从目标跟踪处理的过程看,火控计算机的任务大致归结为四点:确定目标现在点,求取目标运动参数,计算目标提前点坐标(解命中),求取射击诸元。 见公式(1),(2),(3),(4),这些运算包含了大量的正弦和余弦函数的运算。

(1)
目标运动参数公式:
(2)
相对运动情况下求取目标运动参数公式。
计算提前点坐标:
(3)
加了各种修正量后目标运动参数求解。
其中:
(4)

从目标计算的公式可见,正弦、余弦函数参与的运算很多,这里如果采用三角函数单元解算,通过硬件实现三角函数就可以加快函数的计算过程。我们可以根据系统的技术指标,建立多个三角函数解算单元,每一个单元负责一个正弦或余弦三角函数的解算,在计算机系统中建立8或16个三角函数解算单元,就可实现多个目标跟踪的快速处理。
2.2 硬件电路设计
为了加快三角函数的解算,在系统中设计8到16个三角函数单元进行正弦、余弦函数的解算,为此,在系统中设计一个译码器电路,用于计算机指定某一个三角函数单元(正弦芯片单元)进行三角函数计算,见图3 ,三角函数解算单元的选择电路图。

图3 译码器选择其中一个三角函数单元的线路
有了多个三角函数解算单元,它们就可以同时进行多个正弦函数的解算,实现对多个目标的跟踪。
2.3 函数解算单元阵列对系统会不会产生影响
在系统中增加三角函数单元解算正弦和余弦函数,不会产生其它影响,因为函数解算单元是独立的芯片,它通过译码器电路进行选择,地址设计选择计算机中可用字段,阵列中的芯片被选中后,独立工作,互不影响,计算机与正弦芯片是并行工作状态。
2.4 在目标跟踪时三角函数解算单元的应用
如果火控系统进行目标跟踪,假定现在火控系统进行速度分量的解算,见计算公式(5):

ωβDsinε·sinβ+ωβDcosε·cosβ
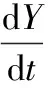
ωβDsinε·cosβ-ωβDcosε·sinβ

(5)
我们可以根据公式(5),将需计算的sin(ε),sin(β),cos(β)和cos(ε)4个函数值,分别指定4个三角函数单元解算,方法是:先把正弦的自变量β,ε换算成相应的地址,再把这个地址送到指定芯片上。然后,再由读指令即可获得该自变量β和ε的函数值。为了方便说明,这里假设β等于30°,ε等于45°,根据上述地址换算公式,可得它们的函数地址分别是30 000和45 000,以十六进制数表示为:7530H和AFC8H,余弦的地址是EA60H和 AFC8H,再用写指令将这些地址分别指定给4个正弦芯片,就可解算出正弦30度和45度,余弦30度和45度的函数值。显然,正弦芯片的工作是与计算机CPU并行的。因为,正弦芯片在自行解算函数值的同时,它不占用CPU,这时,计算机可进行其它工作,这样就加快了目标跟踪中三角函数的解算,所以,速度分量vx,vy,vH的计算CPU只需完成加减乘的计算,复杂的函数计算无需参加。
3 从而使火控系统可快速跟踪解算更多目标
由于三角函数解算单元可以快速的解算三角函数值,这就使目标解算过程中求解三角函数的计算耗时极短,如果在系统中设立多个三角函数单元,使它们各自独立工作,我们就可实现对多个跟踪目标的处理,三角函数解算单元越多,目标跟踪的数量就可大大增加,
4 结束语
在火控计算机中采用硬件解算三角函数,实现正弦、余弦函数的快速解算,目的是加快三角函数的解算,提高火控计算机的处理能力。虽然只是设想,但实践表明,这是实现三角函数解算的最简单方法和途径。今后的研究方向是直接在内存中开辟一段储存区,把正弦函数值依顺序排列在存储区中,解算三角函数值时,由读指令根据函数值的地址直接从这段存储存区(EPPROM)中读取函数值,这样三角函数解算就只需一条读指令即可完成。这实际上是在火控系统中建立了一个函数解算单元,遇到函数解算就用这个函数解算单元进行处理。我们认识到火控系统的创新应该从正弦函数解算的方法上入手,改进正弦的算法才是出路。不然,火控系统的计算仅依靠计算机处理,大家就都处在同一水平,谁也难有超越对方的可能。这一算法不仅在目标跟踪中有显著意义,实际凡是用到三角函数解算的地方都有用,特别是在潜艇水下目标监听和识别,也大量存在三角函数的解算,这里更应该使用这一算法,以提高潜艇早期发现早期识别目标的能力。
[1] 袁岐川,袁 野.新型指挥仪模拟器的分析与研究[A].中国计算机自动测量与控制技术协会[C].第二十届全国测试与故障诊断技术研论文集,2011.
[2] 袁岐川,康建斌. 一种面向查表方式的正弦函数快速算法及应用[A]. Edited by Prof.Yong JIANG,Dr.Kai Liu,Second International Conference on Information and Computing Science (ICIC2009) Volume 5[C].英国·曼彻斯特大学,World Academic Union,2009,5:103-107.
[3] 董志荣.指控系统发展的哲学视野[J].指挥控制与仿真,2008(4):1-5.
[4] 董志荣.目标运动分析新论[Z].连云港 :江苏自动化研究所,2005.
AHardwareSolutionMethodofTrigonometricFunctioninComputer
Yuan Qichuan, Long Weijie, Li Jianfeng
(CSIC 716 Research Institute, Lianyungang 222006,China)
Aiming at the existence of target tracking in a large number of trigonometric function calculations, puts forward to establish trigonometric functions in the fire control computer calculating unit, trigonometric function is realized by using hardware decoding. And trigonometric function calculating unit is a kind of sine function calculating chip. Its core design is based on Angle value address, through hardware look-up table, Value of 0 to 90 degrees of sine function, look-up table. Table look up precision can design to 0.001°, maximum look-up table time is the function of calculating time. Look-up table of time is the biggest function value calculation of time. Cosine look-up table calculation is to use sine the same chip, can look up table according to the relationship between phase difference of 90 degrees. Practice shows that trigonometric function of hardware decoding speed fast, high precision, the common method of the function calculating can be replaced. So, if in the fire control system, design an address decoder circuit, can create multiple trigonometric function calculating unit chip, Through computer data, instructions, the realization of parallel computing for multiple trigonometric function value, thus improve the system of multiple target fast track processing capacity.
trigonometric functions; sine algorithm; chip design; fire control computer
2017-04-05;
2017-05-15。
袁岐川(1958-),四川名山人,高级工程师,主要从事计算机检测与虚拟仪器技术的应用开发方向的研究。
1671-4598(2017)11-0120-03
10.16526/j.cnki.11-4762/tp.2017.11.031
TP274
A

