全平面上(p，q)级随机Dirichlet级数的值分布

黄 婷， 陈 蕾， 郑春雨

(琼台师范学院 数理系, 海南 海口 571123)

全平面上(p，q)级随机Dirichlet级数的值分布

黄 婷， 陈 蕾， 郑春雨

(琼台师范学院 数理系, 海南 海口 571123)

根据全平面上(p，q)级随机Dirichlet级数的定义，通过把全平面上的随机Dirichlet级数映射到单位圆上的随机Dirichlet级数，应用推广的Nevanlinna第二基本定理，证明了全平面上(p，q)级随机Dirichlet级数在一定条件下几乎必然以每条水平直线为无例外小函数的(p，q)级强Borel线，该结论丰富了Dirichlet级数的成果，具有一定的理论意义.

随机Dirichlet级数; (p，q)级； 强Borel线； 小函数.

1 引言与结果

考虑随机Dirichlet级数

(1)

满足0≤λ0lt;λ1lt;λ2lt;…lt;λn↑+∞，s=σ+it，σ及t是实变数，{Xn(ω)}为某概率空间(Ω，A，P)上的独立复随机变量列.

恒假定{Xn}满足下列条件：对∀ngt;0，E(Xn)=0，且存在一正数d，使得

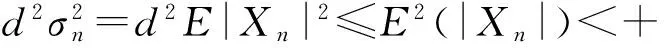
(2)

引进辅助级数

(3)

令

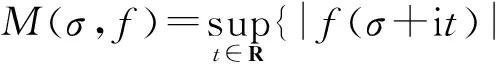
对全平面上解析的级数(2)，令

其中p、q为整数，p≥q≥0.

定义1如果ρ=ρf(p-1，q-1)=0或+∞(p≥q≥0)，而0lt;ρf(p，q)lt;+∞，则称解析函数f(s)有指数对(p，q)，则ρ=ρ(p，q)称为f(s)的(p，q)级.

注：本文仅讨论pgt;q的情形.

由文献[1]中的定理6.6.4可知：若级数(1)满足(2)式及

(4)

那么级数(1)与级数(3)有相同的(p，q)级，且

(5)

本文得到如下结果:

定理1若级数(1)满足条件(2)、(4)和(5)，那么几乎必然每条水平直线{s|Ims=t0}(t0∈R)是fω的没有例外小函数的ρ(p，q)级强Borel线，即对∀ω∈A，∀t0∈R,∀ηgt;0及∀φ∈H有

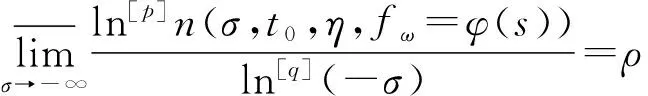
(6)

其中

n(σ，t0，η，fω=φ(s))=
#{s|fω=φ(s)，s∈B*(σ，t0，η)，φ∈H}，

B*(σ，t0，η)={s|Res≥σ}∩B(t0，η)，

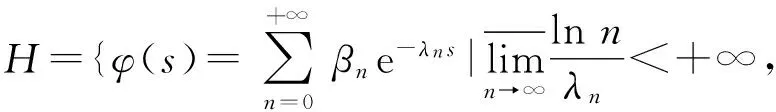
2 引理

给定t0∈R和ηgt;0，考虑映射

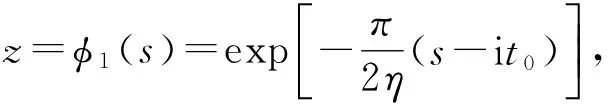
(7)

其逆映射s=Φ1(z)，z=Φ2(W)，令

W=φ(s)=φ2·φ1(s)，s=Φ(W)=Φ1·Φ2(W)，

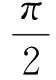
H*(r)={z||z|≤r}∩Hk,k=1，2，

D(R)={W||W|lt;R},R∈(0，1]，

那么Φ(D(1))=B(t0，η).有下面引理，见文献[1].

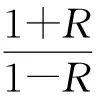
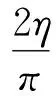
(8)

及

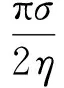
(9)

则映射(7)将级数(1)及∀φ(s)∈H映射为D(1)内的随机解析级数，有

并且Ψ(W，ω)与ψ(W)在D(1)内随机解析，令

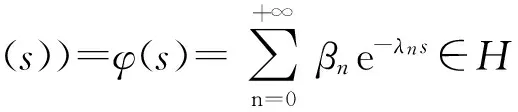
由Nevanlinna第二基本定理推广得到下面引理：

引理2令G(W)和gj(W)(j=1，2)在D(1)内解析且满足

及T(R，gj(W))=o(T(R，G(W)))(R→1)，那么

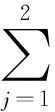
其中R∈(0，1)，A和B是正常数.

由文献[1]中的引理6.7.3可得下面引理:

引理3设随机变量Xn(ω)满足(2)式，那么

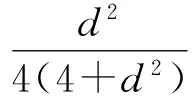
引理4对在D(1)内解析的Ψ(W，ω)有

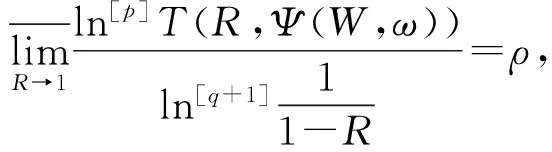
(10)

及∀ψ∈H′至多有一个可能的例外值ψ(W)使下式成立

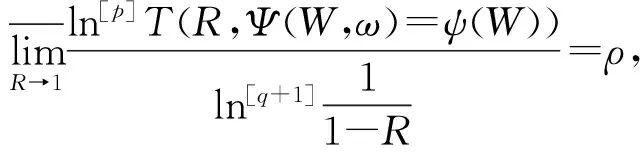
(11)

其中

N(R，Ψ(W，ω)=ψ(W))=

n(μ，Ψ(W，ω)=ψ(W))=

#{W|Ψ(W，ω)=ψ(W)，|W|lt;μ}.

证明共分3步完成证明.

第1步 由(8)和(9)式有

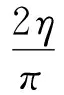
MΨ(R，ω)≤M(σ，fω)，

及

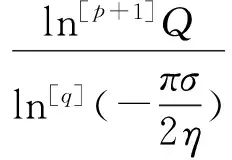
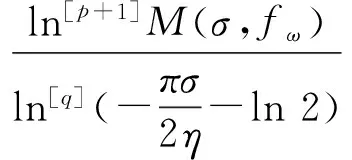
又由文献[1]中的定理6.7.5和定理6.7.6可知，对t∈R，ηgt;0,有

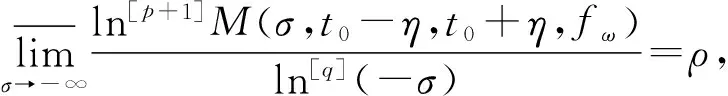
因此有

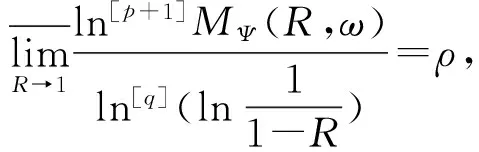
又因为

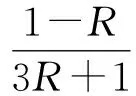
从而

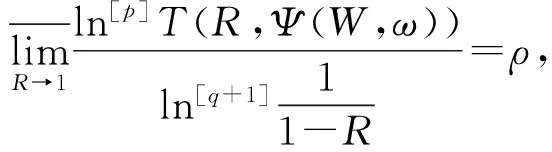
成立.

(12)

其中

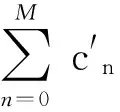
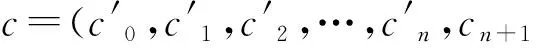
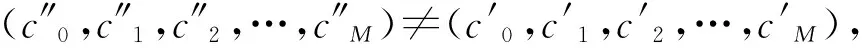
第3步 证明对于D(1)内解析的Ψ(W，ω)及∀ψ(W)∈H′有

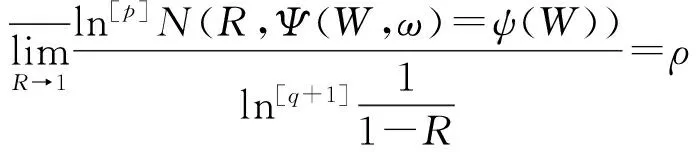
成立.

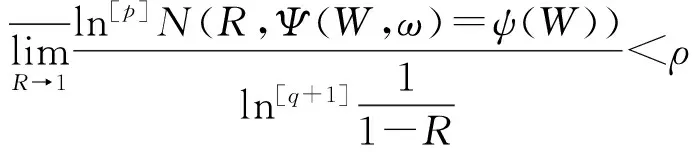
令

s∞={(X0(ω)，X1(ω)，…)|ω∈s}⊂E∞，

只需证P(s)=0.

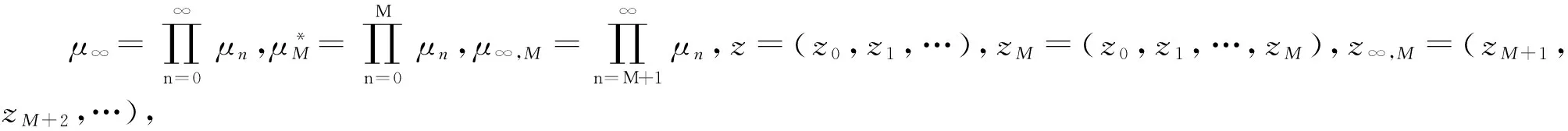
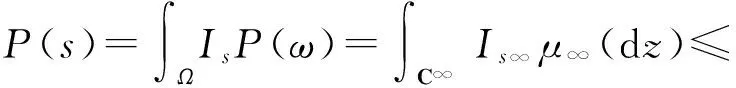
故有P(s)=0，即

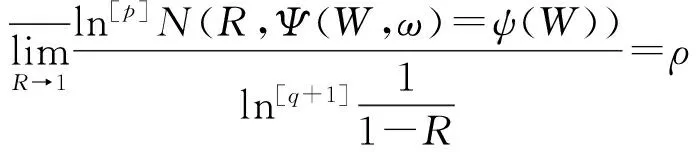
成立.综上引理4得证.

3 定理1的证明

证明根据引理4中N(R，Ψ(W，ω)=ψ(W))与n(R，Ψ(W，ω)=ψ(W))的定义及引理4中(10)式很容易得到

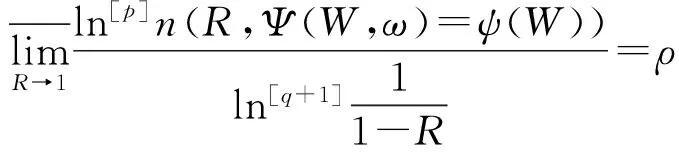
成立，由(8)和(9)式，对∀φ(s)∈H有

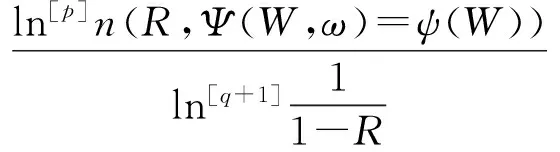
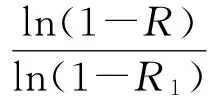
因此(6)式a.s.成立.

选取一个全部由有理数构成的数列{tk}及数列{ηm}(ηm↓0)，类似前面的讨论即可得到定理1成立.

[1] 余家荣,丁晓庆,田范基. Dirichlet级数及随机Dirichlet级数的值分布[M]. 武汉：武汉大学出版社,2004.

[2] 金其余,孙道椿. 全平面上的随机Dirichlet级数的值分布[J]. 数学物理学报,2009,A29(4):1044-1055.

[3] 张洪申,孙道椿. 全平面上随机Dirichlet级数的值分布[J]. 数学学报(中文版),2015,58(5):773-780.

[4] 李云霞. 全平面上q-级随机Dirichlet级数的Borel线[J].四川师范大学学报(自然科学版),2016,39(1):98-102.

[5] 黄婷. 广义级随机Dirichlet级数的值分布[J]. 数学的实践与识,2015,45(18):241-245.

[6] 余家荣. Dirichlet级数及随机Dirichlet级数在水平直线上的增长性[J]. 江西师范大学学报(自然科学版),1995,19(3):189-196.

[7] HUO Y Y, KONG Y Y. On generalized orders and generalized types of Dirichlet series in the right half-plane[J]. Acta Math Sci,2014,B34(1):175-182.

[8] 金其余,孙道椿. 半平面上的Dirichlet级数的(p，q)(R)级和(p，q)(R)下级[J]. 系统科学与数学，2008,28(12):1493-1501.

[9] SUN D C, YU J R. On the distribution of values of random dirichlet series(Ⅱ)[J]. Chin Ann Math,1990,B11(1):33-44.

[10] SUN D C. Common borel points of a meromorphic function and its derivatives in the unit circe[J]. Acta Math Sci,1984,4(2):227-232.

[11] 高宗升,孙道椿. 涉及小函数的随机Dirichlet级数[J]. 数学学报,2003,46(2):397-402.

[12] YU J R. Borel lines of random dirichlet series[J]. Acta Math Sci,2002,B22(1):1-8.

[13] 黄婷,孙道椿. 无限级随机Dirichlet级数的亏函数[J]. 华南师范大学学报(自然科学版),2008(1):29-32.

[14] 黄婷. 一类随机Dirichlet级数的亏函数[J]. 株洲师范高等专科学校学报,2007,12(2):31-44.

[15] 孔荫莹. Dirichlet-Hadamard乘积的q-级和q-型[J]. 数学学报,2009,52(6):1165-1172.

[16] 杨祺,田宏根. 复平面上无限级Dirichlet级数和随机Dirichlet级数的下级[J]. 四川师范大学学报(自然科学版),2008,31(6):680-683.

[17] 张洪申,孙道椿. 右半平面上Laplace-Stieltjes变换的Picard点[J]. 四川师范大学学报(自然科学版),2013,36(2):226-228.

2010MSC:30D30; 30D35

(编辑 余 毅)

On the Distribution of Random Dirichlet Series with (p,q) Orders in the Whole Plane

HUANG Ting, CHEN Lei, ZHENG Chunyu

(DepartmentofMathematicsandPhysics,QiongtaiNormalUniversity,Haikou571123,Hainan)

In this paper, the random Dirichlet series on the whole plane is mapped to the random Dirichlet series on the unit circle by the difinition of random Dirichlet series with (p,q) orders on the whole plane. Using the generalized second Nevanlinna basic theorem, we prove that the random Dirichlet series with (p,q) orders almost surely take every horizontal line as a strong Borel line and without exceptional little functions. This result enriches the theory about Dirichlet series and has a certain theoretical signification.

random Dirichlet series; (p,q) orders; strong Borel line; little functions

O174.5

1001-8395(2017)06-0768-04

10.3969/j.issn.1001-8395.2017.06.010

2016-11-07

海南省自然科学基金(20161007)