解析函数的Schwarz不等式

卢 飞, 周 吉

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

解析函数的Schwarz不等式

卢 飞, 周 吉*

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

主要讨论从单位圆到带形区域0lt;Imf(z)lt;π上的解析函数的Schwarz引理及边界Schwarz引理.

Schwarz引理; 边界Schwarz引理; 解析函数

1 预备知识

在复变函数论中,Schwarz引理是一个非常重要的结果,具有广泛的应用价值.下面所表述的引理被称为经典的内部Schwarz引理.

引理1.1[1]如果函数f(z)在单位圆|z|lt;1内解析,并且满足条件

f(0)=0, |f(z)|lt;1, |z|lt;1,

则在单位圆内恒有

|f(z)|≤|z|,

(1)

且

|f′(0)|≤1.

(2)

f(z)=zeiθ, |z|lt;1,

其中θ为一实常数.

引理1.2[1]若函数f(z)=cpzp+cp+1zp+1+…,cp≠0,p≥1,满足:

1)f(z)在单位圆上解析,

2) 当|z|lt;1时,|f(z)|lt;1;

则

|f(z)|≤|z|p,z∈,

(3)

且

|f(p)(0)|≤p!.

(4)

f(z)=zpeiθ,

其中θ是实常数.

20世纪20年代,一些著名的数学家,如G. Julia[2]、J. Wolff[3]和C. Carethéodory[4]等研究了从单位圆到单位圆内的解析映射在边界的行为,得到了边界Schwarz引理[5].近年来,D. M. Burns和S. G. Krantz[6]、B. N. Örneak[7-8]、R. Osserman[9]等学者也得到了许多好的结果,如:

引理1.3[9]若函数f(z)满足:

1)f(z)在单位圆上解析;

2) 当|z|lt;1时,|f(z)|lt;1;

3)f(0)=0;

4) 存在点b,|b|=1,使得f(z)可连续的延拓到b,且|f(b)|=1,函数f(z)在点b处导数存在;

则

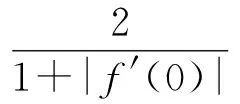
(5)

进一步,当且仅当

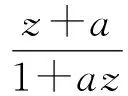
其中0≤a≤1,(5)式中等号成立.

引理1.4[9]若函数f(z)=cpzp+cp+1zp+1+…,cp≠0,p≥1,满足:

1)f(z)在单位圆上解析;

2) 当|z|lt;1时,|f(z)|lt;1;

3) 存在点b,|b|=1,使得f(z)可连续的延拓到b,且|f(b)|=1,函数f(z)在点b处导数存在,

则

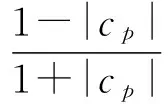
(6)

进一步,当且仅当

f(z)=zpeiθ,

其中θ是实常数,上述不等式等号成立.

本文将研究从单位圆到带形区域0lt;Imf(z)lt;π上的解析函数f(z),得到了相应的Schwarz引理及边界Schwarz引理.

2 主要结果及证明

在下面的讨论中,不妨令

f(z)=u+iv,

其中,|z|lt;1.

定理2.1若函数f(z)在单位圆上解析,满足f(0)=i,且0lt;Im (f(z))lt;π,则

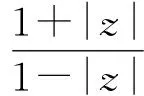
(7)

且

|f′(0)|≤2.

(8)

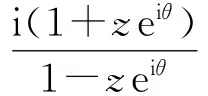
且

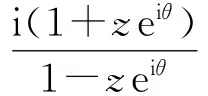
其中θ是实常数.

证明令f(z)=u+iv,其中-∞lt;ult;+∞,0lt;vlt;π.构造函数

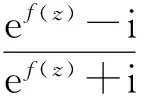
则函数φ(z)在上解析,且

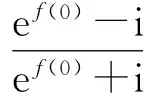
注意到

|ef(z)-i|2-|ef(z)+i|2=-4eu·sinv.

由-∞lt;ult;+∞,0lt;vlt;π,得

-4eu·sinvlt;0,

即

|ef(z)-i|2lt;|ef(z)+i|2,

从而

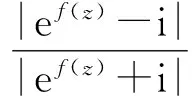
因此,φ(z)在单位圆上解析有

φ(0)=0, |φ(z)|lt;1, |z|lt;1.

由Schwarz引理(引理1.1)得

|φ(z)|≤|z|, |z|lt;1.

由φ(z)的定义得

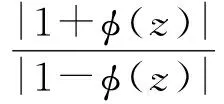
则

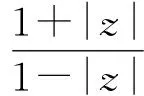
注意到

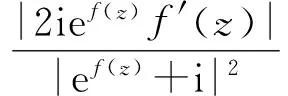
由

得

|f′(0)|≤2.

容易验证:当且仅当

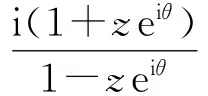
且

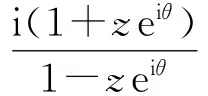
其中θ是实常数,(7)和(8)式中等号成立.

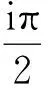
(9)

且

|f(p)(0)|≤2p!.

(10)

且

其中θ是实常数.

证明构造函数

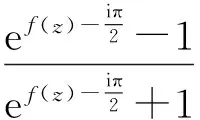
则φ(z)在单位圆上解析,φ(0)=0,且当|z|lt;1时,|φ(z)|lt;1成立.

容易得到:φ(z)有展开式

φ(z)=(cp/2)zp+….

由定理2.1即可得到该命题成立.

定理2.3若函数f(z)在单位圆上解析,满足f(0)=i,且0lt;Im (f(z))lt;π.进一步地,若存在点z0∈∂,函数f(z)在点z0处导数存在,且Im (f(z0))=π(或Im (f(z0))=0),则

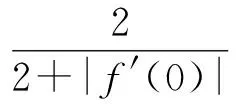
(11)

进一步,当且仅当

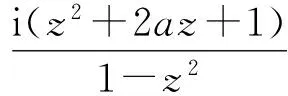
且

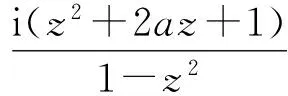
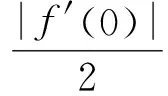
证明构造函数

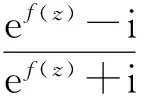
由定理2.1证明过程知:φ(z)在单位圆上解析,φ(0)=0,|φ(z)|≤|z|,|z|lt;1.注意到

由引理1.3有

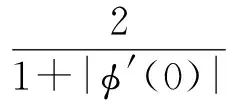
当且仅当

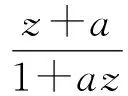
其中0≤a≤1,上述不等式中等号成立.

而

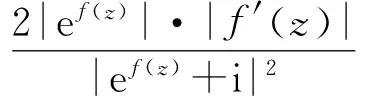
从而

因此

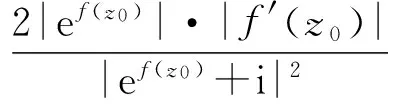
则有

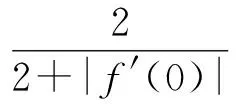
进一步,当且仅当

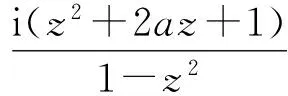
且

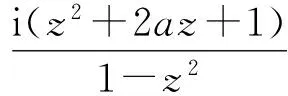
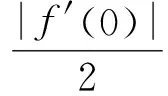
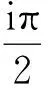
(12)

当且仅当

且

其中θ是实常数,(12)式中等号成立.

证明考虑函数

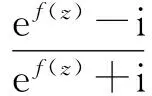
由定理2.1的证明过程知:φ(z)在单位圆上解析,φ(0)=0,|φ(z)|≤|z|,|z|lt;1,且当z0∈∂时,|φ(z0)|=1.从而

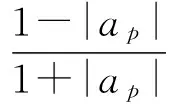
进一步,当且仅当

φ(z)=zpeiθ,

其中θ是实常数,上述不等式中等号成立.

而由

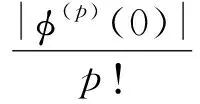
则可得

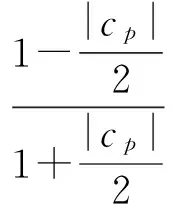
即有

当且仅当

且

其中θ是实常数,上述不等式中的等号成立.

[1] 钟玉泉. 复变函数论[M]. 北京:高等教育出版社,2004.

[2] JULIA G. Extension nouvelle d'un lemma de Schwarz [J]. Acta Math,1920,42(1):349-355.

[3] WOLFF J. Sur une généralisation dun théoréme de Schwarz [J]. C R Acad Sci Paris,1926,182(6):918-920.

[4] CARATHÉODORY C. Theory of Functions of a Complex Variable[M]. New York:Chelsea Publishing Company,1960.

[5] POMMERENKE C. Boundazry Behaviour of Conformal Maps[M]. Berlin:Springer-Verlag,1992.

[6] BURNS D M, KRANTZ S G. Rigidity of holomorphic mappings and a new Schwarz lemma at the boundary[J]. J Am Math Soc,1994,7(3):661-676.

[7] ÖRNEAK B N. Sharpened forms of Schwarz lemma on the boundary[J]. Bull Korean Math Soc,2013,50(6):2053-2059.

[8] ÖRNEAK B N. Carathéodory's inequality on the boundary[J]. Commun Korean Math Soc,2015,20(2):169-178.

[9] OSSERMAN R. A sharp Schwarz inequality on the boundary[J]. Proc Am Math Soc,2000,128(12):3513-3517.

2010MSC:37F50

(编辑 余 毅)

Some Schwarz Inequalities on Analytic Functions

LU Fei, ZHOU Ji

(CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)

In this paper, we discuss about the analytic functions ofinto the strip 0lt;Im (f(z))lt;π and obtain the corresponding Schwarz Lemma and the Schwarz Lemma on the boundary.

Schwarz Lemma; Schwarz Lemma on the boundary; analytic function

O174.51

A

1001-8395(2017)06-0743-04

10.3969/j.issn.1001-8395.2017.06.006

2017-01-24

国家自然科学基金(11371266)、教育部博士点专项基金(20095134110001)和四川省应用基础研究项目(07JY029-013)

*通信作者简介:周 吉(1963—),男,教授,主要从事复分析的研究,E-mail:zhouji@sicnu.edu.cn