基于小波变换的图像双水印算法
刘庆亮 杨树国
(青岛科技大学数理学院,山东 青岛 266061)
基于小波变换的图像双水印算法
刘庆亮 杨树国*
(青岛科技大学数理学院,山东 青岛 266061)
随着信息技术的迅猛发展,数字作品的知识产权保护和信息的安全性愈来愈越重要。本文提出一种基于小波变换的图像双水印算法,首先运用HAAR小波对原始图像亮度分量进行三层离散小波变换,并运用Arnold变换和二维超混沌模型对识别水印进行混沌加密;然后结合小波域内的JND模型,在低频分量中嵌入识别水印,并运用同一密钥在水平分量中嵌入确认水印。实验结果表明,该双水印算法具有良好的不可见性、鲁棒性和安全性,能有效提高图像版权的认证、保护能力。
双水印;Arnold变换;二维超混沌模型;离散小波变换;JND模型
1 引言
随着信息技术和网络的迅猛发展,人们可以很方便地获取想要的数字信息,但随之而来的数字作品的知识产权保护和信息的安全问题也变得愈来愈越重要。
2005年,许斌等提出了一种在图像小波变换域中嵌入双水印的算法[1]。该方法在图像变换域低频分量中嵌入识别水印,在高频分量中嵌入确定水印,该算法能够有效保护图像内容完整和维护图像版权,但是抵抗噪声能力较差。2009年,岳岩等提出了一类基于DCT特性的双水印算法[2],算法结合图像的纹理特性,通过嵌入可见水印和不可见水印实现图像的版权保护和认证,但是水印的不可感知性较差。2013年,陈兴娥等提出在原始图像中嵌入两个数字水印[3],一个是用于图像版权保护的奇异值分解的鲁棒性数字水印,另一个用于图像内容认证的基于图像内容的自适应半脆弱水印,大大提高了数字水印的应用范围和可扩展性。
目前,人们对水印图像的质量要求越来越高,水印的设计要尽可能满足鲁棒性好、不可感知性强的特点,不仅能够有效地保护图像内容完整和维护图像版权,还要保证图片的质量。如文献[4]提出了一种基于混沌的脆弱水印算法,通过修改载体图像的最低有效位来实现水印的嵌入。但是图像原始数据受到影响,图像的不可感知性效果较差。文献[5]提出了一种医学图像认证算法,运用联合稀松编码将水印嵌入到非感兴趣区域,保证了图像的鲁棒性和不可感知性。
鉴于此,本文提出一种基于小波变换的图像双水印算法,以达到有效保护版权和准确认证图像版权的双重目的。该算法首先运用HAAR小波对原始图像的亮度分量进行三层小波分解,运用Arnold变换和二维超混沌系统对识别水印进行加密;然后结合JND模型,将识别水印嵌入到稳健性较好的低频分量中,并将确认水印自适应地嵌入到小波域的水平分量中。水印的嵌入强度由低频系数决定,水印的提取不需要原始图像,可实现水印的自适应嵌入和盲提取功能。实验结果表明,该水印算法具有良好的鲁棒性和不可感知性。
2 相关理论阐述
2.1 离散小波变换[6-8]
小波变换(wavelet transform)是空间(时间)和频率的局部变换,能有效地提取图像的主要信息和分析局部信号。选择小波变换域的低频区嵌入水印,就是考虑到低频区内系数抗干扰能力强的特点。
为了使算法具有较快的运算速度和较好的效果,本文运用HAAR小波对原始图像的亮度值进行三层离散小波变换。图1所示为三层小波分解的示意图。
实验表明,在低频分量中嵌入水印信号对高斯噪声、椒盐、平滑、剪切等攻击表现出较好的鲁棒性。此外,选择不同小波基对嵌入水印性能有很大影响。刘久芬等人研究了水印算法中不同小波基与鲁棒性的关系,其研究结果表明正交基的正则性、消失矩阶数、支撑长度及小波能量在低频带的集中程度对水印鲁棒性的影响极小;其研究结果表明HAAR小波比较合适图像水印。因此本文选择HAAR小波基对载体图像进行分解。
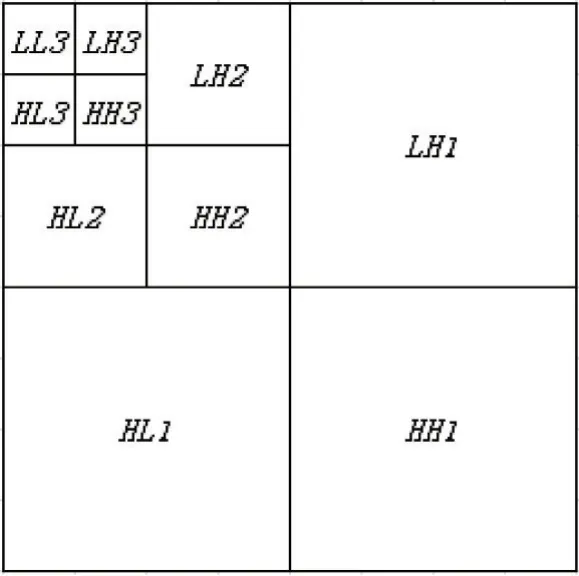
图1 三级小波分解示意图
2.2 Arnold变换[8-10]
为了提高水印信号的安全性,在嵌入水印前需对水印进行加密处理。Arnold变换是一种常用的置乱加密方法,可以减少图像相邻像素之间的关联性,提高水印的鲁棒性。Arnold变换实质上是把(x,y)点的像素信息置换到(x’,y’)点。
对于N×N大小的水印图像,进行n次置乱的公式为:

其解密过程如下:

其中,(x,y)为原始信号,n为n≥1的正整数,置换次数为Arnold变换的密钥K1。
2.3 二维超混沌系统模型[11,12]
目前Logistic映射广泛应用于图像加密领域,但是这种一维混沌系统存在对初值的敏感性较大、密钥空间相对较少、安全性能较低等缺点。为了满足图像水印的鲁棒性和不可感知性,本文采用安全性较好、密钥空间较多的二维离散超混沌系统。
选取的二维离散超混沌系统形式如下:

当a1=1.3;a2=-1.05;a3=1.15;a4=-0.2时,系统处于超混沌状态。进行图像加密时,首先输入初始值为x0、y0的密钥K1,根据式(3)产生序列xn、yn;然后把二维序列降维,变成一维序列sn。为了序列具有较好的扩散均匀度,本文采用的降
维方程为:

然后将其转化成大小为N×N的矩阵s(i,j),(i,j=1,…,N),然后得到二值化的超混沌矩阵t(i,j),矩阵二值化方法如下,其中mean为矩阵中各数均值。

将水印图像对应的二值矩阵w(i,j)与二值化的超混沌矩阵t(i,j)进行异或运算。
2.4 小波域内最小可观测误差(JND)模型[14,15]
通过小波变换将图像分解成低频分量、水平分量、垂直分量和对角分量。在小波域内,人眼对这些分量系数的频率敏感度函数如下:

其中c表示小波分解的层数,d表示小波分解的方向LL,LH,HL,HH。
在小波域内,人眼对亮度的敏感性函数如下:

在小波域内,人眼所能观察图像的纹理掩蔽性函数如下:

其中,
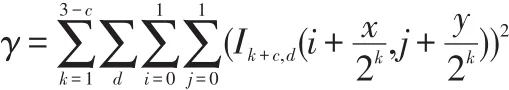
综上得到小波域内人眼视觉系统JND模型,如下:

3 双水印算法描述
本文的双水印算法根据图像的频域和空间域的特点,对原始图像进行三层HAAR小波变换,在图像的小波变换域中分别嵌入识别水印和确认水印,且使这两个水印具有针对性和关联性。
3.1 图像预处理
(1)载体图像预处理
选取大小为M×M的原始图像I,运用HAAR小波基,对其进行三层小波分解,得到原始载体图像的小波系数分量LL3,LH3,HL3,HH3。
(2)识别水印图像预处理
选取N×N大小的二值图像作为识别水印W(x,y),应用Arnold变换对识别水印信号进行n次置乱处理,并用二维超混沌系统进行加密,得到加密后的识别水印信号W’(x,y)。
(3)确认水印图像预处理
首先,利用密钥K3构造长度为N×N的随机正态分布序列Sm,利用随机序列均值将其转化为0和1的二值序列Tm,二值序列的转化方法如下:

然后,运用MATLAB命令“reshape”将Tm转化为N×N的矩阵T。
最后将矩阵T(x,y)与加密的识别水印信号W’(x,y)进行异或运算,并将0全部替换为-1,生成确认水印信号Z。
3.2 信号嵌入与图像重构
(1)识别水印的嵌入
选取小波分解后的LL3方向上(x,y)处的小波系数LL3(x,y)嵌入识别水印信号,嵌入方法如下:
从LL3(x,y)的首项开始嵌入水印信息,公式如下:

其中L(x,y)为含水印信息的低频小波系数;α为嵌入强度,α∈(0,1]。
(2)确认水印的嵌入
取小波变换后载体图像水平方向LH3系数嵌入确定水印信号。嵌入方法如下:
从水平方向系数首项开始嵌入水印信息,公式如下:
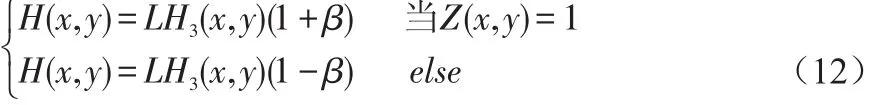
其中H(x,y)为含水印信息的水平小波系数;β为嵌入强度,β∈[0.1,0.5]。
(3)载体图像重构
利用L(x,y)、H(x,y)及其他小波分解系数重构小波系数,得到含水印图像I*。
4 双水印信号提取与检测
(1)识别水印信号提取与检测[1,12]
首先提取出载体图像三层小波分解的低频分量频率系数,利用下面公式还原识别水印信号:
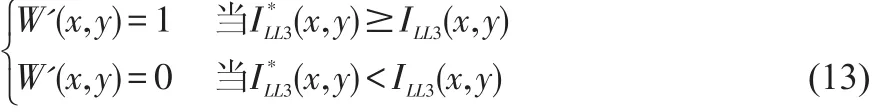
输入密钥K1和K2进行二维超混沌系统和Arnold变换解密过程,得到识别水印图像W(x,y)。
为了检测算法的鲁棒性,采用归一化的相关系数NC值作为该水印算法鲁棒性以及图像认证、版权保护的客观评价指标,其计算公式如下:

若NC值越接近1,则表明提取的识别水印与原始水印相似度越大;反之,相似度越小。
(2)确认水印信号检测[13,14]
首先提取含有水印图像三层小波分解的水平分量系数,并计算其与确认水印信息的相关性,计算方法如下:
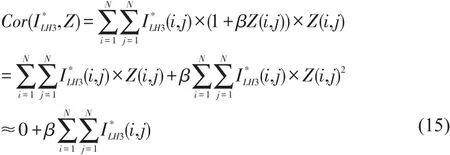
对于待检测图像I',定义如下检测响应度函数:

可以通过给出阈值T,对确认水印进行确认。检测响应度ρ越接近1,越能确认水印信息。
5 实验结果与分析
5.1 实验环境设定与参数选取[15,16]
实验环境为MATLAB2016a,选取512×512的“lena.bmp”图像作为原始载体图像,32×32的二值图像“水印”作为原始识别水印图像,确认水印序列Z的大小为32×32。
实验中,密钥K1的确定:Arnold变换次数n=23;密钥K2的确定:二维超混沌系统参数选取的初值为:x0=0.2,y0=0.7;嵌入强度系数α=0.3,β=0.3;密钥K3的确定:随机正态分布序列Sm,其长度为32×32。
图2中,a为原始图像;b为原始识别水印图像;c为加密的识别水印图像;d为原始图像小波三层分解图像;e为含水印图像,其PSNR值为52.9513,说明该水印算法的不可见性良好;f分别为提取的水印图像,其NC值为1,确认水印检测响应度为1,说明算法鲁棒性较好。

图2 水印嵌入信息图像
5.2 水印不可见性分析
图像PSNR值(峰值信噪比)是最广泛使用的评鉴画质的客观量测法。一般情况下,PSNR的值高的图像质量相对较高,通常,当PSNR值在28以上时,图像质量差异不太显著,当高于35~40时,则肉眼分辨不出差异。本文对三幅不同载体图像进行了分析,分析结果如图3所示。

图3 不同载体图像水印不可见性分析
5.3 算法鲁棒性分析
对水印鲁棒性进行测试分析,对含有水印的lena载体图像作以下各种攻击后得到待测图像。从待测图像以提取识别水印和确认水印。通过识别水印的NC值、确认水印检测响应度ρ的大小,以及载体图像受攻击后的PSNR值,对算法进行鲁棒性分析。攻击类型如下:
(1)随机噪声:载体图像添加均值为0、方差为0.0001的Gauss白噪声干扰;
(2)旋转:图像旋转角度为15°;
(3)剪切:图像左上角剪切掉8×8像素;
(4)中值滤波:用3×3正方形窗口对图像滤波攻击。
测试结果如图4所示:

图4 鲁棒性分析图
图4所示的含水印的lena图像在遭受攻击后的图像质量在一定程度上有明显差异,但是提取的水印图像依然能够辨别,图4中提取的水印NC值依次为0.9576、0.8100、0.7071、0.8591。另外,确认水印的响应度均大于0.7,完全可以判定待测图像确认水印存在,从而可以认为提取的识别水印有效。载体图像遭受不同攻击后,提取的水印的相关参数如表1所示。
为了更好地说明算法的算法优越性,本文对二维超混沌加密和Logistic加密进行了比较,实验结果如表1所示。实验结果表明本文算法效果更好。
为了说明算法鲁棒性,对本文算法与文献[1]进行比较,如表2所示。表2显示的数据显示,本文算法明显优于文献[1],表明本文算法的鲁棒性较好。

表1 水印算法比较分析

表2 算法鲁棒性比较
为了更好地说明算法的鲁棒性,本文对不同载体图像进行了攻击实验,实验结果如表3所示。通过表中数据,不难发现算法对于不同的载体图像,仍然具有良好的鲁棒性。
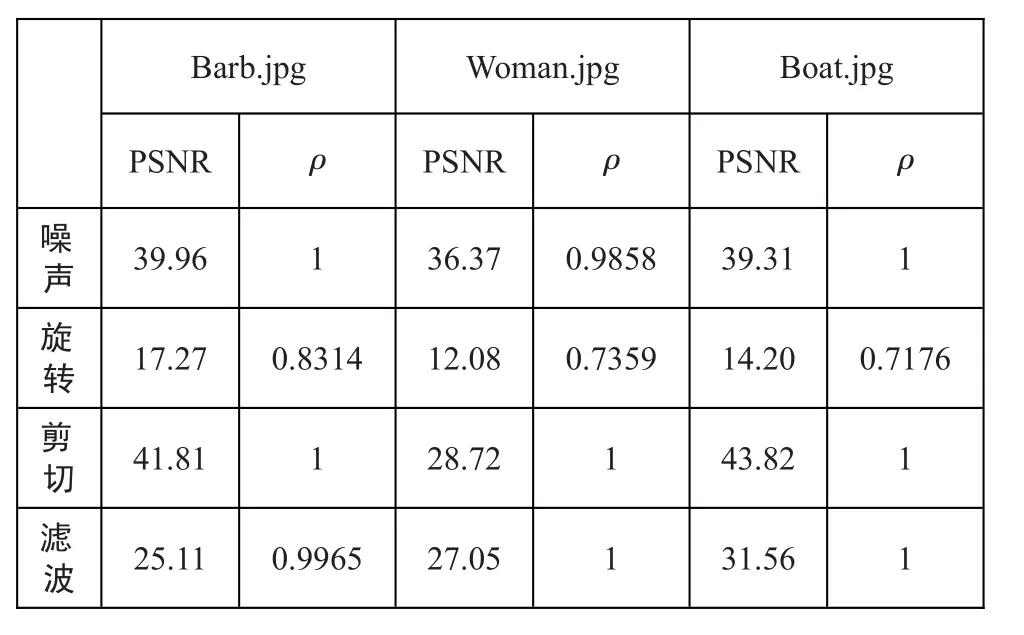
表3 算法鲁棒性分析
6 结束语
本文在小波变换的基础上,提出一种基于JND模型的双水印算法。实验结果表明,该算法不仅具有较快的计算速度,还具有良好的不可见性和鲁棒性。另外,算法通过密钥控制大大提高了算法的安全性,因此,该双重水印检测方法能够有效认证、保护图像版权。
[1]许斌,王润生.基于小波变换的双水印算法[J].计算机工程与科学,2005,27(1):24-26.
[2]岳岩,王希常,刘江.基于频域DCT特性的数字图像双水印算法[J].信息技术与信息化,2009,23(1):62-63.
[3]陈兴娥.图像版权保护和内容认证的数字双水印技术研究[J].廊坊师范学院学报,2013,13(4):38-43.
[4]Mantratzis C,Orgun M,Cassidy S.Separating XHTML content from navigation clutter using DOM-structure block analysis[C]//Hypertext 2005,Proceedings of the,ACM Conference on Hypertext and Hypermedia,September 6-9,2005,Salzburg,Austria.DBLP,2005:145-147.
[5]Tareef A,Al-Ani A,Nguyen H,et al.A novel tamper detectionrecovery and watermarking system for medical image authentication and EPR hiding[J].Conf Proc IEEE Eng Med Biol Soc,2014:5554-5557.
[6]吴婧瑾.基于小波的数字水印的研究实现[D].成都:电子科技大学,2008.
[7]周国瑞.小波与数字水印理论及应用研究[D].成都:电子科技大学,2010.
[8]刘衍琦,詹福宇.MATLAB图像与视频处理实用案例详解[M].成都:电子工业出版社,2015.
[9]张颖,杨玥.Arnold双置乱图像加密算法[J].辽宁工程技术大学学报,2013,32(10):1429-1432.
[10]吴玲玲,张建伟,葛琪.Arnold变换及其逆变换[J].微计算机信息,2010,26(14):206-208.
[11]肖振久,李南,王永滨,等.基于超混沌的医学图像篡改定位零水印算法[J].计算机工程与应用,2017,53(7):115-120.
[12]周蕊,于晓明,焦占亚.一种基于混沌序列的数字图像加密算法[J].微电子学与计算机,2010,27(12):62-64.
[14]肖亮,韦志辉,吴慧中.一种利用人眼视觉掩盖的小波与数字水印[J].通信学报,2002,23(3):100-106.
[13]杨树国.鲁棒图像数字水印技术的研究[D].哈尔滨:哈尔滨工程大学,2003:25-33.
[14]申丽平.基于离散小波变换的数字图像双水印算法[J].计算机工程,2011(s1):128-130.
[15]胡彦,陈昭炯.MATLAB在数字水印中的应用[J].计算机工程,2003,29(7):184-186.
[16]秦襄培,郑贤中.MATLAB图像处理宝典[M].北京:电子工业出版社,2011.
Image Dual WatermarkingAlgorithm Based on Wavelet Transform
Liu Qingliang Yang Shuguo*
(Qingdao University of Science and Technology,Qingdao 266061,Shandong)
With the rapid development of information technology,digital media intellectual property protection and information security are more and more important.In this paper,an image dual watermarking algorithm based on wavelet transform is proposed.First,the luminance component of original image is subjected to three discrete wavelet transforms(DWT)by HAAR wavelet.And the watermark is identified for chaotic encryption by Arnold transform and two-dimensional hyper-chaotic model.Then,the watermark is embedded in the low frequency component according to the JND model.And the watermark is embedded in the horizontal component according to the same key.The experimental results show that the double watermarking algorithm has good invisibility,robustness and security,and can effectively improve the image copyright authentication and protection ability.
dual watermark;Arnold transform;two-dimensional hyper-chaotic model;DWT;JND model
TP391.4
A
1008-6609(2017)10-0001-05
刘庆亮(1991-),男,山东临朐人,硕士研究生,研究方向为图像水印、视频水印。
*通讯作者:杨树国(1970-),男,山东曹县人,博士,教授,研究方向为数字水印、图像处理。
山东省重点研发计划项目,项目编号:2015GGX101020;青岛市科技发展计划项目,项目编号:KJZD-13-27-JCH;山东省研究生教育创新计划项目,项目编号:SDYY16010;山东省教育科学“十二五”规划课题,项目编号:YBS15014。

