解题探究活动不能仅仅留下一个结论
——谈分段求和破解含绝对值项的数列求和方法
江苏 王怀学
解题探究活动不能仅仅留下一个结论
——谈分段求和破解含绝对值项的数列求和方法
江苏 王怀学

一、分组分段求和是解决问题的本质策略
含有绝对值的问题中,首要任务就是分类讨论.对于一个数列{an},如果有些项是正数,有些项是负数,在求数列{|an|}的前n项和的时候,就需要把正数项和负数项分组求解.这是此类问题求解首先要明确的一个问题.
【例1】在等差数列{an}中,a1gt;0,a10·a11lt;0,若此数列的前10项和S10=36,前18项的和为S18=12,则数列{|an|}的前18项的和T18=________.
【解析】由已知得公差dlt;0,a10gt;0,a11lt;0,所以等差数列{an}单调递减.
所以T18=S10+|a11|+|a12|+…+|a18|
=S10-(a11+a12+…+a18)
=S10-(S18-S10)
=2S10-S18
=72-12=60.

【变式1】在数列{an}中,已知an=n+11,n∈N*,求|a1|+|a2|+|a3|+…+|an|.
【解析】当n∈N*时,an=n+11gt;0成立,
则数列{an}可以看成首项为12,公差为1 的等差数列.

二、前k项为正数的分段讨论
求数列{|an|}的前n项和,就是要搞清楚数列{an}的项的正负,再分组分段求和,而数列{an}的项的正负决定着分组讨论的不同情形,因此我们要对数列{an}的项的正负展开讨论.
【例2】在公差为d的等差数列{an}中,已知a1=10,且a1,2a2+2,5a3成等比数列.
(Ⅰ)求d,an;
(Ⅱ)若dlt;0,求|a1|+|a2|+|a3|+…+|an|.
【解析】(Ⅰ)依题意得(2a2+2)2=5a1a3,4(a1+d+1)2=50(a1+2d),(11+d)2=25(5+d),解得d=4或d=-1,于是an=4n+6或an=11-n.
(Ⅱ)由(Ⅰ)知,当dlt;0时,an=11-n,
①当1≤n≤11时,an≥0,

②当n≥12时,anlt;0,


【点评】当数列的项有正负之分,就需要先判断正负再求和.当前k项为正,后n-k(ngt;k,n,k∈N*)项为负时,可得Tn=|a1|+|a2|+…|ak|+|ak+1|+…+|an|=(a1+a2+…+ak)-(ak+1+ak+2+…+an)=Sk-(Sn-Sk)=2Sk-Sn.
【变式2】已知数列{an}的前n项和为Sn=32n-n2,求数列{|an|}的前n项和Tn.
【解析】因为Sn=32n-n2,所以当n≥2时,Sn-1=32(n-1)-(n-1)2,
作差得,an=33-2n,a1=S1=31也满足上式.
所以,数列{an}的通项公式为an=33-2n,所以数列{an}单调递减.

即当n≤16时,angt;0;当n≥17时,anlt;0.
所以当n≤16时,数列{|an|}的前n项和Tn=Sn=32n-n2;
又S16=256,所以当n≥17时,Tn=2S16-Sn=n2-32n+512.

三、前k项为负数的分段讨论
数列的前k项的正负,其实从本质上同求和没有什么区别,都是要进行分段求解,前k项都是正的,那么就把前k项单独拿出来,并直接表示为Sk,余下的提取负号,还是可以用Sn-Sk表示;同理前k项都是负数,方法也是同样,不需要背记公式.
【例3】数列{an}的前n项和Sn=n2-100n.
(Ⅰ) 数列{an}是什么数列?
(Ⅱ)设bn=|an|,求数列{bn}的前n项和Tn.
【解析】(Ⅰ)因为Sn=n2-100n,所以
an=Sn-Sn-1=n2-100n-(n-1)2+100(n-1)=2n-101(n≥2),
当n=1时,满足条件,所以an=2n-101,
所以数列{an}是首项为-99,公差为2的等差数列.
(Ⅱ)因为bn=|an|=|2n-101|,

所以当n≤50时,Tn=-Sn=-n2+100n;
当n≥51时,
Tn=T50+a51+a52+…+an
=-S50+a51+a52+…+an
=-S50+Sn-S50
=Sn-2S50
=n2-100n+5 000,

【点评】前k项为负,后n-k(ngt;k,n,k∈N*)项为正的数列求和,首先按绝对值的代数意义去绝对值符号,可得
Tn=|a1|+|a2|+…+|ak|+|ak+1|+…+|an|
=-(a1+a2+…+ak)+(ak+1+ak+2+…+an)
=-Sk+(Sn-Sk)=Sn-2Sk.
【变式3】在数列{an}中,已知an=2n-25,n∈N*,求 |a1|+|a2|+|a3|+…+|an|.
【解析】设数列{an}的前n项和为Sn,数列{|an|}前n项和为Tn.

所以,对数列{|an|}来说,

当n≥13时,Tn=|a1|+|a2|+…+|a12|+|a13|+…+|an|=-(a1+a2+…+a12)+(a13+a14+…+an)=-2(a1+a2+…+a12)+(a1+a2+…+an)=Sn-2S12=n2-24n+288.
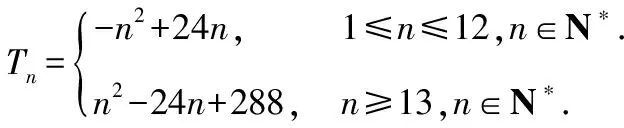

江苏省赣榆县海头高级中学)

