从几个不同角度思考一道平面向量题
江苏 张路民
从几个不同角度思考一道平面向量题
江苏 张路民
最近笔者听了一堂高三一轮复习课《平面向量基本定理和坐标表示》,课堂上师生们在共同探讨一道习题时,经历了一些波折也遇到了一些困难,其中有些思路中途夭折未能进行到底.笔者细细琢磨了一番,觉得甚是有趣,现将笔者的一些想法分享如下:


分析:这道题考查的知识点是平面向量的基本定理,研究的策略无非是基底法与几何法.课堂上学生从不同角度进行思考,但最终不是因为过程繁琐就是思路卡壳难以进行到底.


下面笔者就这个问题分别从坐标法、基底法和几何法三个不同的角度对本题加以诠释.
一、坐标法
向量是既研究大小又研究方向的量,利用坐标法解决向量问题往往能够使问题简化,另外我们都知道解决填空题有别于解答题,只要能算出答案就可以,其中特值特例就是一种非常有效且简易的手段.本题可以将问题特殊化即把梯形看成直角梯形,为使计算方便还可以将边长取特殊值.
解法1:将梯形ABCD看成直角梯形,且设AB=4,AD=2,如图建立直角坐标系,结合2DC=AB,M,N分别是DC,BC中点,则A(0,0),B(4,0),D(0,2),C(2,2),M(1,2),N(3,1).



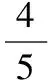
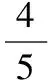
小结:本题巧妙地利用了梯形的任意性,采用特殊代替一般的处理原则,使问题解决简捷快速.因此,这一方法对于解决选择题和填空题非常有效,但此方法处理并不具有普遍性,需要解题者自己去把握与权衡.
二、基底法
平面向量基本定理:如果e1、e2是同一平面内不共线的两个向量,那么对于这个平面内的任一个向量a,有且只有一对实数λ1、λ2,使a=λ1e1+λ2e2.不共线的向量e1、e2叫做表示这一平面内的所有向量的一组基底.因此在具体操作过程中,选取哪两个向量作为e1、e2以及如何用选取的e1、e2表示a,将是解决问题的关键,也是难点所在.



三、几何法
向量题是高中数学的重点、热点考点.解题时可以从数与形两个角度考虑,代数法证明思维量小但计算量都较大.相对于代数法,几何法的优势在于直观且计算量小,找到向量的几何意义后,问题就能迎刃而解,它是求解向量问题的有效策略之一,对于运用几何法解决向量题应该引起我们足够的重视.

解法4:如图,延长AN与DC的延长线交于点E.

因为DC∥AB,点N是BC的中点,
所以CEAB,AN=NE,即
又因为点M是DC中点且AB=2CD,


解法5:如图,连接BD,连接MN并延长与AB的延长线交于点E.


解法6:如图,延长AM,BC交于点E,

因为AB∥DC,且AB=2DC,
又点M为DC中点,所以AE=4ME,BE=4CE,





江苏南京市大厂高级中学)

