一道全国高考真题的变式探究与推广
安徽 杨续亮 苏岳祥
一道全国高考真题的变式探究与推广
安徽 杨续亮 苏岳祥
一、试题再现

(Ⅰ)求C的方程;
(Ⅱ)设直线l不经过P2点且与C相交于A,B两点,若直线P2A与直线P2B的斜率的和为-1,证明:l过定点.
二、试题规律分析
三、试题解法赏析

下面对本题的第二问作些探究:
证法一:直线方程的斜截式视角
设直线P2A和直线P2B的斜率分别为k1,k2且k1+k2=-1,
①当直线l的斜率不存在时,设l:x=t由题设知|t|lt;2且t≠0,A(t,yA),B(t,-yA),

得t=2,此时l过椭圆右顶点,不存在两个交点,故不满足.
②当直线l的斜率存在时,设l∶y=kx+m(m≠1),A(x1,y1),B(x2,y2),

整理得(1+4k2)x2+8kmx+4m2-4=0,


=-1,
又m≠1,所以m=-2k-1,
此时Δ=-64k,存在klt;0使得Δgt;0成立.
所以直线l的方程为y=kx-2k-1,
当x=2时,y=-1,所以l过定点(2,-1).
证法二:平移坐标系视角


因为直线P2A与直线P2B的斜率的和为-1,

所以2m-2n=1,平移后得直线经过定点(2,-2),平移前的直线方程为m-2n=1,
所以平移前的直线经过点(2,-1).
【评注】这种解法,很好地体现了减元思想和整体思想,在设定直线l的方程也可以设为点斜式,两点式直接求解.
四、试题的变式探究

(Ⅰ)求椭圆C的方程;
(Ⅱ)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值.
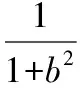

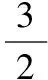




又直线AF的斜率与AE的斜率互为相反数,
在上式中以-k代k,可得

所以直线EF的斜率


【评注】直线AE的斜率与AF的斜率互为相反数时,即k1+k2=0时,直线EF的斜率为定值.

(Ⅰ)求椭圆C的方程;
(Ⅱ)当r变化时,①求k1·k2的值;②试问直线BD是否过某个定点?若是,求出该定点;若不是,请说明理由.

又a2-b2=c2,



对于直线AD:y=k2x+1,

于是k1,k2是方程(1-r2)k2-2k+1-r2=0的两实根,故k1·k2=1.
考虑到r→1时,D是椭圆的下顶点,B趋近于椭圆的上顶点,故BD若过定点,则猜想定点在y轴上.
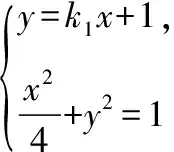


直线BD的方程为
令x=0,


【评注】直线AB,AD的斜率之积为k1k2=1为定值时,直线BD过定点.

(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设N(0,2),过点P(-1,-2)作直线l交椭圆C异于N的A,B两点,直线NA,NB的斜率为k1,k2,证明k1+k2为定值.

由余弦定理得
|F1F2|2=|MF1|2+|MF2|2-2|MF1||MF2|cos60°
=(|MF1|+|MF2|)2-2|MF1||MF2|(1+cos60°),


由|F1F2|=4得c=2,从而b=2.

(Ⅱ)证明:当直线l的斜率存在时,设斜率为k,

得(1+2k2)x2+4k(k-2)x+2k2-8k=0,
设点A(x1,y1),B(x2,y2),




=4,

综上,k1+k2=4为定值.
【评注】过点P(-1,-2)作直线l交椭圆C异于N(0,2)的A,B两点,直线NA,NB的斜率为k1,k2,可以得到k1+k2为定值.
从2017年全国卷高考试题和3个变式我们得到如下结论:
在这个问题中,如P是椭圆上的一点,A,B是两动点,那么,PA,PB斜率之和为定值时或者之积为定值时,直线AB是否经过定点呢?通过探究,发现:






从变式试题可以看出,这里的4个结论逆命题同样成立,只是叙述的方式上稍作调整,请读者自己完成.
五、试题的类比探究
【变式4】已知抛物线C:y2=2px(pgt;0)的焦点F(1,0),O为坐标原点,A,B是抛物线C上异于O的两点.
(Ⅰ)求抛物线C的方程;


所以抛物线C的方程为y2=4x.
(Ⅱ)证明:①当直线AB的斜率不存在时,



所以A(8,t),B(8,-t),此时直线AB的方程为x=8.
②当直线AB的斜率存在时,设其方程为y=kx+b(k≠0),设点A(x1,y1),B(x2,y2),






即y=k(x-8).
综上所述,直线AB过定点(8,0).

过抛物线y2=2px上点的任意一点P(x0,y0)作两条直线PA,PB与抛物线交于点A,B,其中,PA,PB,AB斜率都存在,分别记作k1,k2,k,则有如下结论:



读者可以参照2017年全国理20和变式题的证明方法证明这三个结论.

(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l:y=kx+m与椭圆C相交于A,B两点(于A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点,求证直线l过定点,并求出该定点的坐标.


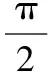

(Ⅰ)求轨迹C的方程.



安徽省安庆市岳西县汤池中学)

