从一道高考选择题看“反证思想”的应用
赵 维
陕西
从一道高考选择题看“反证思想”的应用
赵 维

2017年江苏省高考化学试卷第15题,是一道以化学平衡为载体的计算型选择题,重点考查学生对化学平衡常数的理解应用以及从题目中提取有用信息的能力。考查角度新颖,解题思想与以往按部就班的正向思维完全不同,侧重于对学生逆向思考能力的考查。下面,我们以此题为例,看看数学中的“反证思想”(先假设某命题不成立,并证明该命题与已知结论不一致,从而说明假设命题错误,则证明原命题正确)在其中的应用。文章最后,对这道高考原题进行改编,改编后的选项既有对“反证思想”的应用,也有对题中已有信息的加工提炼,在训练学科思想方法的同时,也能较好地培养学生应用信息解决具体问题的能力。
【真题】温度为T1时,在三个容积均为1 L的恒容密闭容器中仅发生反应:

实验测得v正=v消耗(NO2)=k正c2(NO2),v逆=v消耗(NO)=2v消耗(O2)=k逆c2(NO)·c(O2),k正、k逆为速率常数,受温度影响。下列说法正确的是
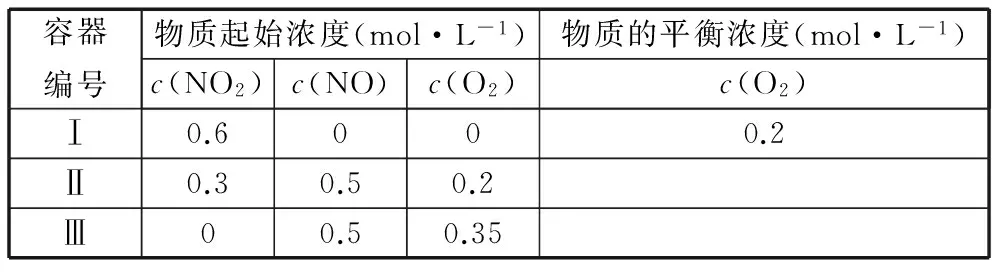
( )
A.达平衡时,容器Ⅰ与容器Ⅱ中的总压强之比为4∶5
C.达平衡时,容器Ⅲ中NO的体积分数小于50%
D.当温度改变为T2时,若k正=k逆,则T2>T1
答案:CD
分析:此题乍一看,好像考查等效平衡,但仔细分析,是以信息为载体,重点考查对化学平衡常数的理解应用。
A选项:要求容器Ⅰ与容器Ⅱ平衡时的总压强之比,一般的思考程序是分别求出容器Ⅰ、Ⅱ平衡时气体的总物质的量,再根据阿伏加德罗定律的推论可知:恒温恒容时,压强之比等于物质的量之比。容器Ⅰ中的反应情况可根据三段式法轻松获得。

起始浓度(mol·L-1) 0.6 0 0
转化浓度(mol·L-1) 0.4 0.4 0.2
平衡浓度(mol·L-1) 0.2 0.4 0.2
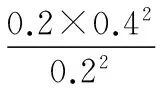
分析容器Ⅱ中的数据,如果直接求平衡后气体的总物质的量,常规方法是:先求出起始时的浓度商Q,将Q与K作比较,判断反应进行的方向,再将转化的量设为未知数,根据K的表达式列方程求解。进行上述操作就会发现,所列方程为一元三次方程,很难求解,所以正向思维在该题中是行不通的。
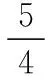

起始浓度(mol·L-1) 0.3 0.5 0.2
转化浓度(mol·L-1) 2x2xx
平衡浓度(mol·L-1) 0.3-2x0.5+2x0.2+x
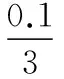
C选项:同理分析,要想得到容器Ⅲ中平衡后各成分的物质的量,通过三段式法依然很难获得。所以类比A、B选项的解题思路,采用反证思想处理。假设平衡时容器Ⅲ中NO的体积分数(物质的量分数)为50%,O2转化浓度为xmol·L-1,则有:

起始浓度(mol·L-1) 0 0.5 0.35
转化浓度(mol·L-1) 2x2xx
平衡浓度(mol·L-1) 2x0.5-2x0.35-x
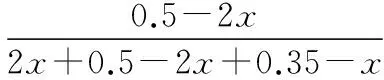
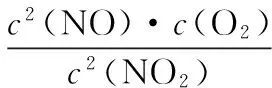
【改编题】题目已知条件与真题一样,对四个选项重新设置。

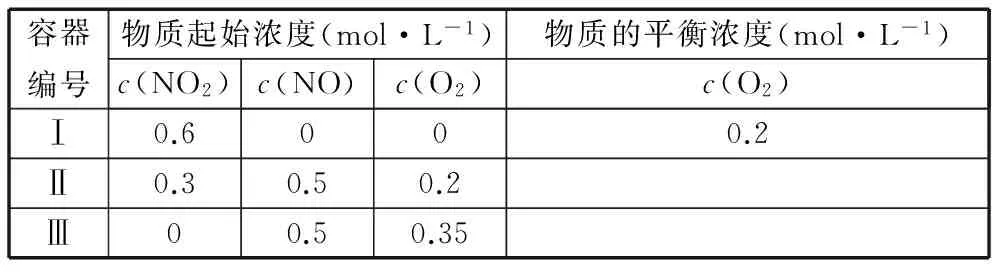
( )
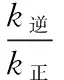
B.达平衡时,容器Ⅱ与容器Ⅲ中总压强之比为20∶17
C.容器Ⅱ中起始平衡正向移动,达平衡时,容器Ⅱ中NO2的转化率比容器Ⅰ中的小

答案:C
分析:A、D选项主要根据题中信息[v正=v消耗(NO2)=k正c2(NO2),v逆=v消耗(NO)=2v消耗(O2)=k逆c2(NO)·c(O2)]
分析;B、C选项应用反证思想解决。
应用已知信息分析AD选项:

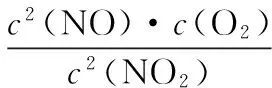
应用“反证思想”分析B、C选项:
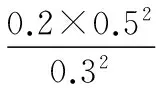
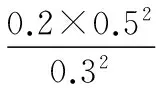

起始浓度(mol·L-1) 0.3 0.5 0.2
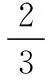
平衡浓度(mol·L-1) 0.1 0.7 0.3
【总结】“反证思想”是一种数学思想,但也为部分化学计算分析题提供了一条清晰明了的解题思路。“反证思想”着重培养的是学生的逆向思维,它可以引导学生突破思维定势,培养学生的质疑精神与创造能力。

陕西省渭南高级中学)

