基于分数阶极值搜索的光伏最大功率跟踪控制

蔡兴龙，马铭磷

（湘潭大学信息工程学院，湘潭 411105）

基于分数阶极值搜索的光伏最大功率跟踪控制

蔡兴龙，马铭磷

（湘潭大学信息工程学院，湘潭 411105）

针对光伏阵列获取最大功率点过程动态响应速度和稳态跟踪精度二者之间不能达到平衡的问题，提出一种基于分数阶极值搜索控制（FO-ESC）的光伏阵列最大化功率点跟踪方法。该方法主要利用分数阶理论提高极值搜索过程的收敛速度和鲁棒性；与整数阶极值搜索控制（IO-ESC）相比，其降低了算法的复杂性。为了验证所提方法的有效性，在Matalb/Simulink中搭建仿真模型进行仿真分析。结果表明，所提方法与IO-ESC相比具有更快的收敛速度和鲁棒性，能够应用于光伏发电工程。

光伏阵列；最大功率跟踪点；分数阶；极值搜索

近年来，国内外学者提出了众多的最大功率点跟踪 MPPT（maximum power point tracking）算法[1-9]。定点电压跟踪法和光伏PV（photovoltaic）阵列组合法是最为简单的控制算法，虽然可以对最大功率点进行快速跟踪，但是忽略了温度的影响，同时实时性很差[2-3]。扰动观察法算法本身控制结构简单，被测参数少，容易实现，改进和优化的方法比较多，但是系统在最大功率点附近会产生振荡，步长的选择也会影响跟踪的速度，同时环境因素造成功率损失且可能发生误判[4]。电导增量法在扰动观察法基础上进行了改进，通过修改逻辑判断式减小了振荡，但是步长和阈值选择上存在一定的难度[5]。另外，针对光伏阵列复杂的非线性的特点，利用处理非线性问题的方法来解决最大功率问题，如模糊逻辑控制法、神经网络法、粒子群算法，但是在最大功率跟踪应用过程中，缺乏成熟的理论支持和学习能力，存在一定的局限性[6-9]。分数阶理论的成熟和应用，一定程度上解决非线性问题，特别在自适应控制方面。例如分数阶自适应滑模控制[10]和分数阶自适应高增益控制[11]。

基于成熟的分数阶理论，本文在自适应控制的基础上通过分数阶极值搜索控制FO-ESC（fractional order extreme seeking control）光伏阵列的最大输出功率，相比于整数阶极值搜索控制IO-ESC（integer order extremum seeking control）方法，提高了控制系统性能和不增加系统的复杂性。相对于其他控制方法更易于实现和提高光伏阵列在获取能量过程中抗干扰性和太阳辐射的不确定性。本文分析了光伏阵列的等效模型和MPPT分数阶极值搜索，最终通过对比实验验证FO-ESC的可行性。

1 光伏阵列模型

光伏阵列是由一系列的光伏电池通过串并联组成，通过光伏阵列的物理结构和输出特性，可得其数学模型[12-15]。图1为一个实际光伏阵列的等效电路。

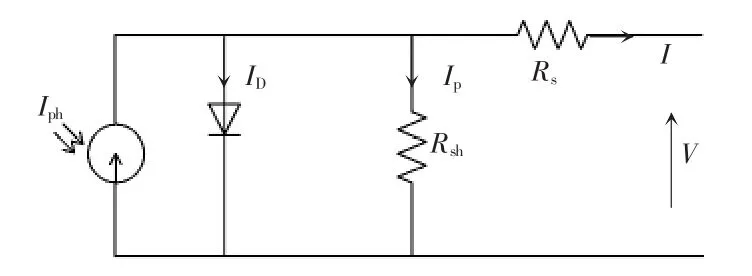
图1 光伏阵列等效电路Fig.1 Equivalent circuit of PV array

光伏阵列PV输出电流可表示为

其中：

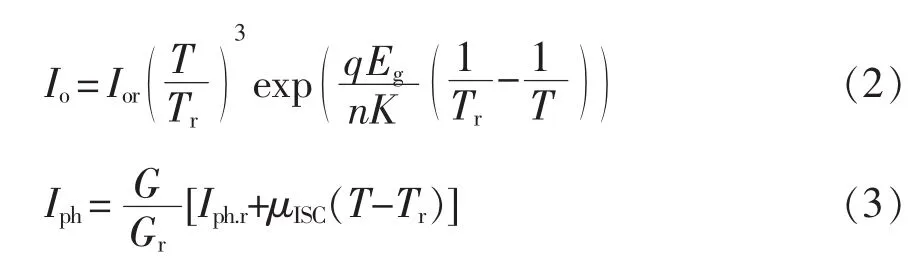
式中：K为玻尔兹曼常数；T为光伏单元表面温度；n为光伏阵列中半导体器件pn结系数；Io为光伏阵列反向饱和电流；Rsh为光伏阵列等效旁路电阻；Rs为光伏阵列等效串联电阻；Ior为在Tr温度下的反向饱和电流；Eg为半导体带隙基准能量；Iph,r为给定光照和温度下的的光生电流；μISC为短路电流温度系数。

在25℃，光照强度1000 W/m2下，光伏阵列输出特性曲线如图2所示。

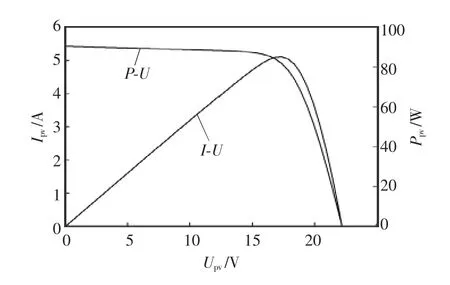
图2 光伏阵列I-U曲线和P-U曲线Fig.2 I-U and P-U curves of PV array

2 分数阶极值搜索

2.1 分数阶微积分

分数阶微积分是整数阶微积分的推广，整数阶微积分是分数阶微积分的特例。在研究非线性系统时，用分数阶数学模型描述的动态系统要比整数阶数学模型描述更加精确。研究过程中对分数阶微积分概念提出了在连续和离散下的两种定义[16]。

（1）分数阶 Grunwald-Letnikow（GL） 离散定义数学表达为

（2）分数阶 Riemann-Liouville（RL）连续定义数学表示达为

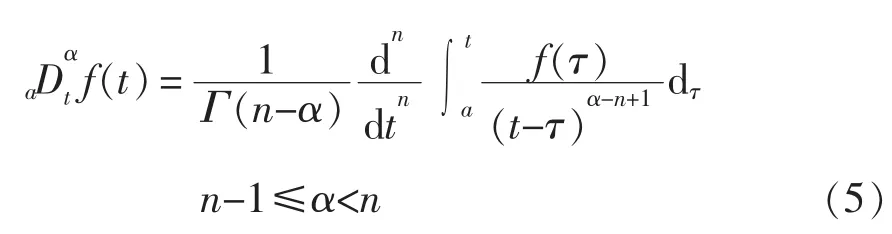
式中：n为大于α的最小整数；Γ（·）为伽马函数。

2.2 极值搜索控制方法

自适应控制中极值搜索方法是通过滤波和驱动信号以达到控制某些未知或不确定系统[17]，结构框图如图3所示。在输入加入正弦干扰信号添加到估计信号中，其相对于输出也会产生一个正弦干扰信号。如果输出的扰动信号出现在极值点两侧，输入输出同相位或者相差180°相位。扰动信号出现在极值点时，输出信号的频率是原来的2倍，且输出功率最大。通过梯度估计来改变输入，计算当前的输出，并与前次输出作比较，确定扰动方向搜索最大值。整个控制回路中增加滤波器来减少扰动，增加输出的精确度。然而由于低通滤波器和积分器是串联的，滤波器对收敛速度没有影响，只是减小估计信号的振荡幅度[18]。由于不影响系统整体的分析，所以在分析过程中将低通滤波器忽略。在文献[18]简化模型分析可知，整数阶线性反馈回路中，优化点 β*和误差信号两者的关系可表达为

其中，

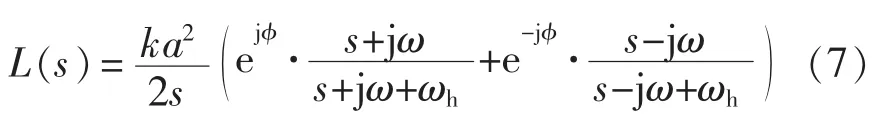
式中：φ为扰动信号的相位延迟；ω为扰动频率、a为扰动信号幅值、k为梯度增益、ωh为滤波器上限截止频率和ωl为下限截止频率，通过结构框图，假设扰动信号没有信号延迟，可知

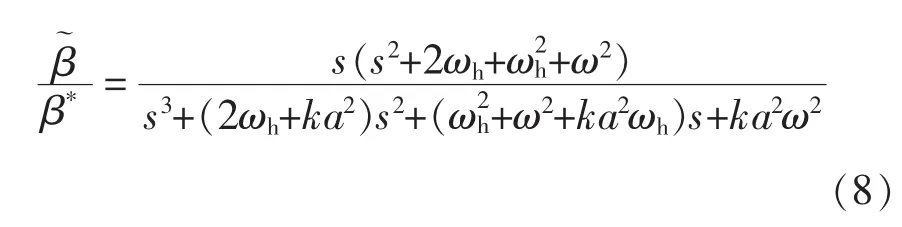
分析式（8），由稳定性判据可知当k＞0时，系统处于稳定。

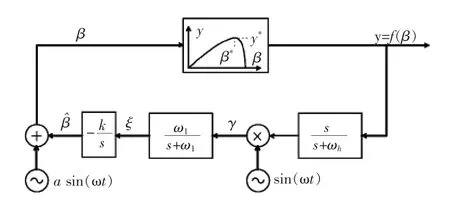
图3 周期扰动极值搜索算法框图Fig.3 Block diagram of periodic perturbed extremum seeking algorithm

尽管不同的整数阶极值搜索算法在解决非线性和自适应控制上取得了很大的进步，但是很多时候无法达到理想的效果[18]。实际应用中为了获得最优性能的极值搜索控制回路，参数ω、α、k、ωh和ωl必须被充分校准[19-21]。虽然较大幅值a或者k可以提高极值搜索的收敛速度，但过大的a和k增加了扰动信号的振幅，降低了系统对抗外部和内部的干扰。根据式（4）和式（5）引入分数阶参数ε，在动态系统中采用分数阶极值搜索线性化模型分析，提高了系统稳定性和响应速度。分数阶梯度估计，分数阶滤波器和极值搜索优化器组成了分数阶极值搜索系统，结构框图如图4所示。

系统的数学模型可表示为

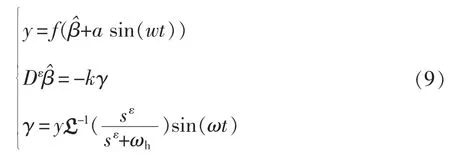
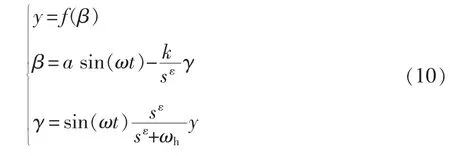
极值点 f（β*）=0 时，由式（10）、式（11）可知 y=f（β*）＋（β*-β）2。文献[18]中整数阶线性化模型推导可知分数阶线性化模型，假设误差信号asin（ωt），由式（10）、式（11）推导可知

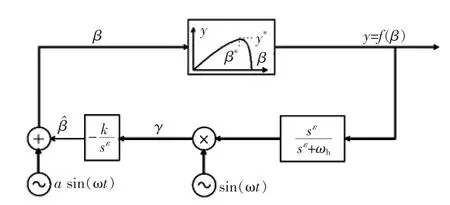
图4 分数阶极值搜索算法框图Fig.4 Block diagram of fractional order extremum seeking control scheme

简化模型分析分数阶线性反馈回路，优化点β*和误差信号两者的关系可表达为

通过结构框图分析，假设扰动信号没有信号延迟，则有

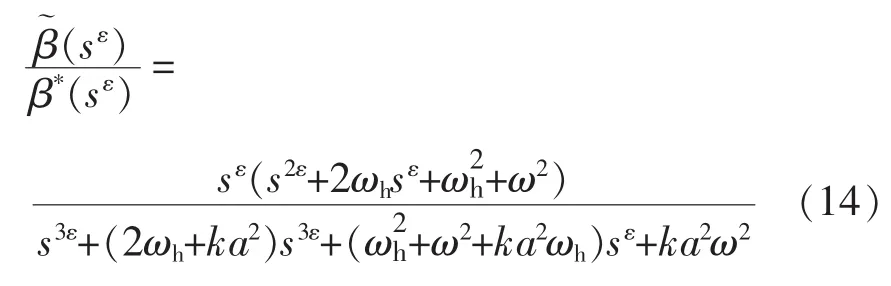
整数阶系统的稳定性区域不同于分数阶系统的稳定性区域，如果特征多项式的所有根都位于复杂的s平面的虚轴的左边，整数阶系统稳定。在文献[22-23]中，整数阶系统是分数阶系统的特例，整数阶稳定的区域分数阶一定稳定。分数阶系统的传递函数是复变量s分数次幂的准特征多项式，由于分数阶系统的特征方程式是一个关于复变量的函数，通过映射整数阶系统稳定分析方法，s变换分析所有特征根，采用复域中的幅角原理可知分数阶系统在幅角|φ|＞επ/2 是稳定的。

3 分数阶极值搜索控制的MPPT

第2.2节分析可知，极值搜索过程最重要的是参数的设计，分别是自适应增益k、振幅a、激励信号角频率ω以及高通滤波器截至频率ωh。a和k直接影响着系统的收敛速度，同时k的大小直接影响着系统的稳定性。将4个参数放入待优化函数进行分析，经过大量仿真得到k和a单独变化与输出函数的变化的关系。由图2可知，光伏阵列输出功率随着光照和温度，呈现着单峰值变化而变化，为获得最大极值点，提高光伏阵列的跟踪速度和减小最大功率点的功率振荡，实现最大功率输出。光伏阵列温度一定时，光伏阵列输出电压和输出电流的乘积作为极值搜索模块的输入，通过梯度估计输出电压，同时计算此时功率并与前次功率作比较，确定是否达到最大功率，并形成一个反馈回路。在Matlab/Simulink环境下对控制算法进行仿真，仿真模型如图5所示。

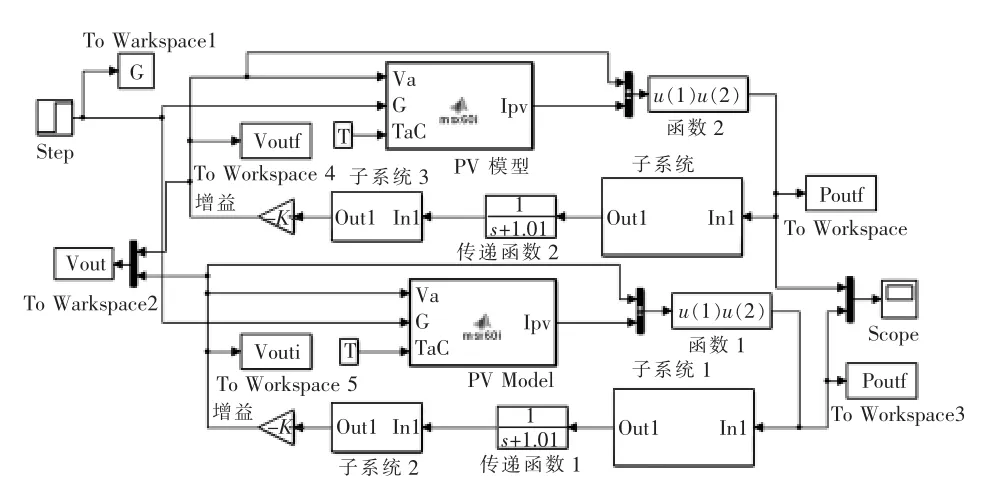
图5 FO-ESC和IO-ESC仿真模型Fig.5 Simulation model of FO-ESC and IO-ESC

4 仿真结果与分析

为验证整数阶极值搜索控制策略和分数阶极值搜索控制策略算法的有效性，在Matlab/Simulink模型中进行公平的比较，两种控制方法运行在相同的条件下，使用相同的整定值，具体参数如表1和表2所示。

表1 光伏阵列性能参数Tab.1 Specification parameters of PV cell

表2 极值搜索参数Tab.2 Extremum seeking parameters

在光照强度1 000 W/m2条件下,在ε=0.9和1.0时，f（β）输出曲线如图6所示。从图6中可以看出，FO-ESC和IO-ESC的极值点跟踪时间t1和t2和输出最大功率点时间t3和t4；FO-ESC比IO-ESC的收敛速度快，并且FO-ESC搜索极值点的速度几乎是IO-ESC的2倍，而且FO-ESC动态稳定性优于IO-ESC。这表明了FO-ESC不采用额外的反馈环路或其他辅助算法的条件下，相比于其他算法提高了算法的性能。

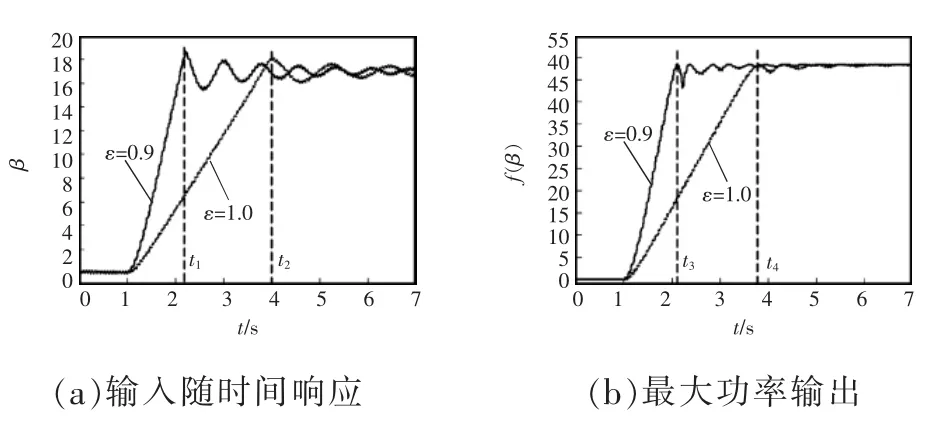
图6 FO-ESC和IO-ESC仿真结果对比Fig.6 Comparison of simulation results between FO-ESC and IO-ESC

进一步分析阶次对FO-ESC的影响，ε在0.82～0.94的仿真结果如图7所示。由图可见，系统在稳定区域中，随着分数阶阶次的减小，系统的反应速度和上升时间都减小。

文献[4]中扰动观察法跟踪光伏阵列最大功率如图8所示，可以看出，与图6中FO-ESC方法相比较，响应速度和稳态跟踪精度都低于FO-ESC最大功率点跟踪。

图7 不同分数阶ε比较结果Fig.7 Differernt values of fractional order ε

图8 扰动观察法输出功率Fig.8 Output power of perturbation and observation method

FO-ESC和IO-ESC动态仿真结果对比如图9所示。由图可见，在25℃下，随着光照强度的变化，不同ε下，FO-ESC比IO-ESC的收敛速度快，并且FO-ESC搜索极值点的速度和动态稳定性明显优于IO-ESC。

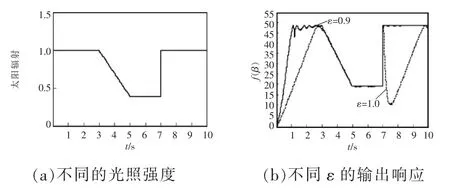
图9 FO-ESC和IO-ESC动态仿真结果对比Fig.9 Comparison of dynamic simulation results between FO-ESC and IO-ESC

5 结语

本文分析提出了一种利用分数阶极值搜索控制跟踪光伏阵列输出最大功率，并和整数阶极值搜索控制跟踪光伏阵列最大功率进行比较。仿真结果表明FO-ESC与IO-ESC相比降低最大功率点附近的振荡，提高了系统的鲁棒性和整体的收敛性，减少了功率损失，提高了光伏阵列的转化效率。

[1]周林,武剑,栗秋华,等.光伏阵列最大功率点跟踪控制方法综述[J].高电压技术,2008,34（6）:1145-1154.Zhou Lin,Wu Jian,Li Qiuhua,et al.Survey of maximum power point tracking techniques for photovoltaic array[J].High Voltage Engineering,2008,34（6）:1145-1154（in Chinese）.

[2]余世杰,何慧若,曹仁贤.光伏水泵系统中CVT及MPPT的控制比较[J].太阳能学报,1998,19（4）:394-398.Yu Shijie,He Huiruo,Cao Renxian.A comparison between CVT and MPPT control in photovoltaic water pumping system[J].Acta Energiae Solaris Sinica,1998,19（4）:394-398（in Chinese）.

[3]Hart G W,Branz H M,Cox C H.Experimental tests of open-loop maximum-power-point tracking techniques for photovoltaic arrays[J].Solar Cells,1984,13（2）:185-195.

[4]刘邦银,段善旭,刘飞,等.基于改进扰动观察法的光伏阵列最大功率点跟踪[J].电工技术学报,2009,24（6）:91-94.Liu Bangyin,DuanShanxu,Liu Fei,et al.Photovoltaic array maximum power point tracking based on improved perturbation and observation method[J].Transactions of China Electrotechnical Society,2009,24（6）:91-94（inChinese）.

[5]张澧生,施佳,施大发.一种改进INC和MPC的光伏最大功率点跟踪算法[J].电源学报,2014,12（2）:95-100.Zhang Lisheng,Shi Jia,Shi Dafa.A photovoltaic MPPT based on improved INC and MPC algorithm[J].Journal of Power Supply,2014,12（2）:95-100（in Chinese）.

[6]Hussein K H,Muta I,Hoshino T,et al.Maximum photovoltaic power tracking:an algorithm for rapidly changing atmospheric conditions[J].IEE Proceedings-Generation,Transmission and Distribution,1995,142（1）:59-64.

[7]Veerachary M,Senjyu T,Uezato K.Feedforward maximum power point tracking of PV systems using fuzzy controller[J].IEEE Transactions on Aerospace and Electronic Systems,2002,38（3）:969-981.

[8]Veerachary M,Senjyu T,Uezato K.Neural-network-based maximum-power-point tracking of coupled-inductor interleaved-boost-converter-supplied PV system using fuzzy controller[J].IEEE Transactions on Industrial Electronics,2003,50（4）:749-758.

[9]Chen Yang,Smedley K M.A cost-effective single-stage inverter with maximum power point tracking[J].IEEE Transactions on Power Electronics,2004,19（5）:1289-1294.

[10]Yin Chun,Chen Yangquan,Zhong Shouming.Fractional-order sliding mode based extremum seeking control of a class of nonlinear systems[J].Automatica,2014,50（12）:3173-3181.

[11]Ladaci S,Loiseau J J,Charef A.Fractional order adaptive high-gain controllers for a class of linear systems[J].Communications in Nonlinear Science and Numerical Simulation,2008,13（4）:707-714.

[12]Tan Y T,Kirschen D S,Jenkins N.A model of PV generation suitable for stability analysis[J].IEEE Transactions on Energy Conversion,2004,19（4）:748-755.

[13]司新跃,陈青,高湛军.基于分段线性的光伏阵列等效模型[J].电网技术,2014,38（4）:947-951.Si Xinyue,Chen Qing,Gao Zhanjun.A piecewise linearization based equivalent model of photovoltaic array[J].Power System Technology,2014,38（4）:947-951（in Chinese）.

[14]Al-Gizi A G.Comparative study of MPPT algorithms under variable resistive load[C]//2016 International Conference on.Applied and Theoretical Electri-city（ICATE）,IEEE,2016:1-6.

[15]Heydari-Doostabad H,Keypour R,Khalghani M R,et al.A new approach in MPPT for photovoltaic array based on extremum seeking control under uniform and non-uniform irradiances[J].Solar Energy,2013,94（4）:28-36.

[16]Podlubny I.Fractional differential equations[C]//Mathematics in Science and Engineering.1999.

[17]Moase W H,Manzie C,Nesi D,et al.Extremum Seeking From 1922 To 2010[C]//Control Conference.IEEE,2010:14-26.

[19]Lei Peng,Li Yaoyu,Seem J E.Sequential ESC-based global MPPT control for photovoltaic array with variable shading[J].IEEE Transactions on Sustainable Energy,2011,2（3）:348-358.

[20]Hu Yun’an,Zuo Bin,Li Jing.A novel chaotic annealing recurrent neural network for multi-parameters extremum seeking algorithm[C]//International Conference on Neural Information Processing.Springer Berlin Heidelberg,2006:1022-1031.

[21]Ariyur K B,Krstic M.Real-time optimization by extremumseeking control[M].Hoboken:John Wileyamp;Sons,2003.

[22]Petras I,Grega S,Dorcak L.Digital fractional order controllers realized by PIC microprocessor:Experimental results[C].Proceedings of the International Carpathian Control Conference（ICCC03）.High Tatras,Slovak Republic,2003:873-876.

[23]Tavazoei M S,Haeri M.A note on the stability of fractional order systems[J].Mathematicsamp;Computers in Simulation,2009,79（5）:1566-1576.

蔡兴龙

蔡兴龙（1992-），男，通信作者，硕士研究生，研究方向：能量收集和DC/DC变换器的集成电路设计等,E-mail:yanjiuxues hu@outlook.com。

马铭磷（1978-），男，博士，副教授，研究方向：射频集成电路设计，E-mail：min glin_ma@xtu.edu.cn。

A Novel Maximum Power Point Tracking Scheme for Photovoltaic Systems Under Fractional Order Extremum Seeking Control

CAI Xinglong,MA Minglin
（College of Information Engineering,Xiangtan University,Xiangtan 411105,China）

Aiming at the balance between the dynamic response speed and the steady-state tracking accuracy of the maximum power point of the photovoltaic（PV） array,a PV-maximized power point tracking（MPPT） method based on fractional order extreme seeking control（FO-ESC） is proposed.This method mainly uses the fractional theory to improve the convergence speed and robus-tness in the process of extremum search,and reduce the complexity of the algorithm compared to integer order extremum seeking control（IO-ESC）.In order to verify the effectiveness of the proposed method,a simulation model is established in Matlab/Simulink for simulation analysis.The results not only show that the proposed method has better convergence speed and robustness than IO-ESC,but also can be applied to photovoltaic power generation project.

photovoltaic cell;maximum power point tracking（MPPT）;fractional order;extremum seeking

10.13234/j.issn.2095-2805.2017.6.43

TM914.4

A

2017-02-23；

2017-08-20

湖南省自然科学基金资助项目（2015JJ2140，2015J J2142）

Project Supported by Natural Science Foundation of Hunan Province,China（2015JJ2140,2015JJ2142）