光伏发电自治微电网逆变器的谐波均流控制

张纯江，郭忠南，郭吉平，张 丽，王晓寰

（1.燕山大学电气工程学院，秦皇岛 066004;2.佳木斯大学信息电子技术学院，佳木斯 154007）

光伏发电自治微电网逆变器的谐波均流控制

张纯江1，郭忠南1，郭吉平2，张 丽1，王晓寰1

（1.燕山大学电气工程学院，秦皇岛 066004;2.佳木斯大学信息电子技术学院，佳木斯 154007）

首先定性分析了微电网逆变器的功率传输特性，证明了微电网逆变器均流控制最关键的是解决各DGs（distributed generations）线路阻抗不平衡时的均流问题，进而提出了一种简单可行的电流直接前馈式均流控制策略，不仅省却了传统下垂控制中所需要的功率计算与电压合成计算，而且可以在确保频率恒为50 Hz的前提下实现并联逆变器间的电流均衡；然后详细分析了虚拟阻抗对均流的作用，提出无滤波器的谐波均流控制，并将其与有滤波器的谐波均流算法进行了对比分析；最后，采用Matlab/Simulink仿真软件进行了仿真验证。仿真结果证明了该控制策略的合理性与有效性。

自治微电网；接口逆变器；谐波均流；虚拟阻抗

光伏电池板发出的直流电通过接口逆变器变换成为交流电，实现并网或独立运行，给负载供电。随着微电网技术的发展，多个光伏逆变器可组成微电网，当微电网与大电网连接时实现并网运行，当微电网与大电网断开时形成独立运行。本文中的自治微电网即是指后一种情况。目前微电网独立运行下的光伏接口逆变器均流控制研究多是集中于线性对称负载，有关微网为非线性负载供电的研究还很少。随着电力电子技术的发展，以整流性负载为代表的非线性负载日益增多，而非线性负载导致电压畸变的根源在于逆变器系统的等效输出阻抗不为0的固有特性。如何保证此类工况下的逆变器输出波形质量及谐波均流亟待解决。

根据特性划分，非线性负载主要有两类：一类是瞬间产生大电流的瞬时突变性负载；另一类是产生非正弦周期电流性负载。整流装置作为目前谐波电流的最主要来源，兼有上述两类负载的特点[1-3]。所以，本文以三相不控整流桥负载为研究对象进行微电网光伏逆变器的控制策略的研究很有代表性。

关于微电网系统带非线性负载时的多逆变器均流控制问题，已有学术研究成果主要分为设置谐波补偿逆变器和加入虚拟阻抗两种方法。文献[4]采用将谐波电流提取后与电压闭环控制器的输出共同作为电流环给定的办法，实现了无互联线逆变器并联系统中的谐波功率控制；文献[5-6]采用三相H桥式逆变器作为补偿分布式发电DG（distributed generation），补偿微电网中的不平衡及非线性负荷，该方法可以避免本地不平衡负荷及非线性负荷对微电网系统其他端点处的电压波形质量的影响，也省去了谐波功率的均分控制，但对补偿DG容量及稳定性提出了更高的要求，如果此台DG从微电网中解列，则此控制系统将崩溃。采用虚拟阻抗的方法[7-9]中，文献[7]将基波与谐波分别提取后，通过加入基波虚拟电感和谐波可变虚拟电阻的方法实现谐波功率均分控制，同时，为补偿谐波均分控制对电压质量的不良影响，采用低带宽通信技术来补偿负载端的电压，以提高系统电压正弦度；文献[10]采用低通滤波器实现系统等效输出阻抗在低频段呈感性、高频段呈阻性，从而避免微电网系统带非线性负载时的谐波均流及电压畸变问题。

本文先对单台逆变器波形质量控制进行简单介绍，然后从定性角度分析微电网逆变器的功率传输特性，进而提出一种电流直接前馈式均流控制策略。然后，从虚拟阻抗角度详细对比分析已有虚拟阻抗理论与本文虚拟阻抗理论，从而证明本文所提策略不仅适用于基波均流，而且适用于谐波均流。

1 逆变器波形质量控制

图1为三相三线制逆变器主电路拓扑，图中，Lf为滤波电感，r为等效电阻，Cf为滤波电容，iLa、iLb、iLc为三相电感电流，uoa、uob、uoc为逆变器三相输出电压，ioa、iob、ioc为逆变器三相输出电流。由于自治运行微电网的接口逆变器需要提供系统的电压支撑，故本文选择逆变器的输出电压闭环反馈控制作为系统的外环，以保证供电系统的电压质量。

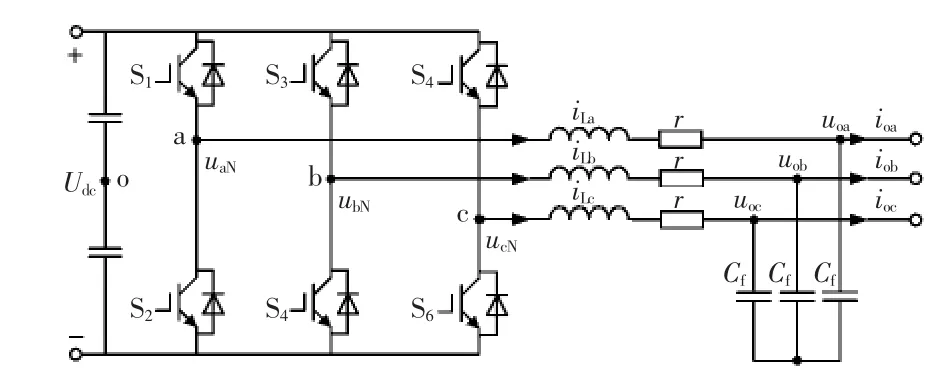
图1 三相三线制逆变器主电路拓扑Fig.1 Circuit topology of three-phase three-wire inverter

选择电感电流闭环反馈控制作为系统内环，增加系统响应速度。由三相逆变器dq坐标系的数学模型可知，逆变器是一个强耦合系统，为简化控制器设计,加入前馈解耦控制，那么d、q轴控制完全独立，可分别设计。同时，经dq旋转变换后，逆变器输出电压的基波分量会转变为直流量，而比例积分PI（proportional integral）控制器实现简单、效果好，故本文选择PI控制器作为电压环的基波控制器。

本文的非线性负载条件下的系统，负载电流d、q轴分量中包含有6ω次的谐波分量，而逆变器的输出阻抗不可能为0，故流过的谐波电流会产生谐波压降，导致逆变器输出电压波形畸变，所以必须对此进行控制。由内模原理可知，单纯采用PI控制，无法实现6ω次谐波分量的无差追踪。研究表明，基于内模原理而产生的比例谐振PR（proportional resonance）控制器可以保证正弦信号的无差控制。

综上，本文选择带有前馈解耦的电压PI控制作为外环、电感电流P控制作为内环的双闭环控制系统的基础上，采用补偿控制的概念，在电压外环控制器中加入6ω次谐振控制器，以补偿5、7次谐波的影响，提高电压供电质量。电压控制器采用PIR控制器，表达式为[11]

式中：Kp为控制器比例系数；Ki为控制器积分系数；Kr6为控制器谐振系数。

图2 三相逆变器的双闭环控制结构框图Fig.2 Block diagram of double closed-loop control for three-phase inverter

图3所示为PI与PIR控制器的频率特性对比。由图3可以看出，谐振控制器只在6ω频率点起作用，并可补偿一定的超前相角；系统在其他频率段，尤其是低频段，增益、系统剪切频率与相角裕度、高频抗干扰能力等方面仍然由PI控制器决定。

图3 PI与PIR控制器的bode图Fig.3 Bode plots of PI and PIR controllers

PI控制器决定系统的动态响应和稳定性，而谐振控制器主要影响系统的稳态特性。所以，可以分开进行PI控制器和R控制器的参数设计，最终再调试整合即可。

2 均流控制

2.1 功率传输理论

图4所示为2台逆变器并联系统简化示意。图中，v1、v2分别为 DG1、DG2输出电压；v1h、v2h分别为DG1、DG2线路压降；voh为负载端的供电电压；ioh为负载电流；i1h、i2h分别为 DG1、DG2输出电流；Z1h、Z2h分别为 DG1、DG2等效输出阻抗，h（=1，2，…，n）表示电流谐波次数。

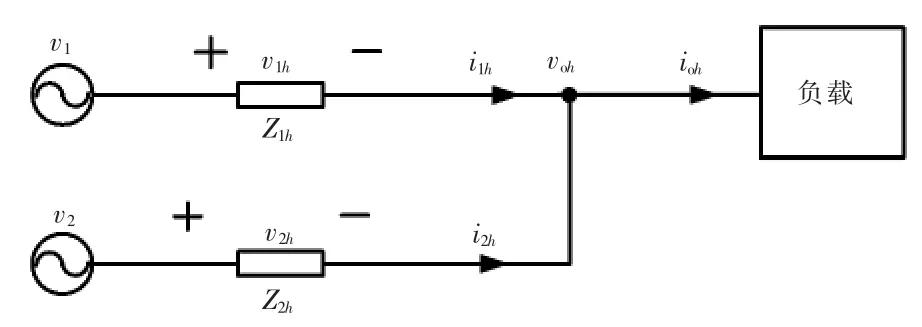
图4 逆变器并联简化示意Fig.4 Simplified diagram of parallel inverters

以往的并联功率传输理论都是采用相量计算的形式来推导出逆变器输出有功功率、无功功率与逆变器输出电压三要素之间的关系式，以此寻求合理的均流控制算法。此方法可以定义为定量分析，其分析结果直观、充分、有力，但由于其是相量计算，故该方法不适用于非线性负载工况。本文从另一视角（定性）进行功率传输特性分析，寻求一种适用于各类负荷的功率理论。

分析适用于负载为线性对称、不对称及非线性各种情况，则线路压降与逆变器输出电压之间关系为

由图4可以分析如下：

（1）若 v1=v2，根据式（2）可知 v1h=v2h，为了使得i1h=i2h，必须满足 Z1h=Z2h。

（2）若 v1≠v2，根据式（2）可知 v1h≠v2h，为了使得 i1h=i2h，必须满足 Z1h≠Z2h。

（3）综合（1）和（2）：若 v1=v2，且 Z1h=Z2h，那么必然使得i1h=i2h。

电压电流双闭环控制下的逆变器具备良好的跟踪性与抗扰动性，也就是说，即便因为系统响应速度、参数误差等因素导致某一时刻的v1≠v2，逆变器的双闭环系统总是试图自我调节使得v1=v2。那么，如果想要功率输出均衡i1h=i2h，必须满足Z1h=Z2h。如果不满足，逆变器的双闭环控制系统的电压无差调节作用与并联均流调节作用的调节方向恰好相反，所以必然存在矛盾，导致系统不稳定。众所周知，微电网系统区别于逆变器并联系统的最大特点就是微电源（如光伏逆变器）和负载的分散性，微电网的结构随着微电网内的微电源和负荷的切入切出而变化，也就是说Z1h≠Z2h是常态，因而自治微电网逆变器均流控制最为关键的问题是如何确保线路阻抗不均衡时，系统仍然能够实现均流；同时，也可以得出结论，线路阻抗不均衡时，要保证其功率输出均衡，必然结果就是v1≠v2。

逆变器若均分负荷，必须保证各DG输出电压对负载电流的抗干扰能力减弱，让负载电流在输出电压上产生反向调节作用，最终彼此之间取得一个平衡，方法就是下垂控制。现在普遍意义上的下垂控制，就是从电压的幅值、频率与相角这三要素出发，分析逆变器输出电流（功率）与这三者之间的关系，从而构造下垂控制算法以实现负载对电压的一种制衡，实现系统稳定运行，并均衡分担负载需求。

应用广泛的下垂控制结构为“功率-电压-电流”三环结构，与双闭环结构相比，动态响应速度慢，同时功率反馈环节含有低通滤波器导致动态过程存在超调[12]。由于存在上述缺点，本文试图跳出这种格局，从电压电流双环出发，寻求一种简单而又可行的方法，既保证系统稳定，又能有效均衡负载。该控制可以避免系统频率随电网结构变化而波动的问题，同时比传统电压频率下垂算法具备更快的暂态响应能力，削弱了暂态的超调及振荡现象。虽然此均流控制为有差均流控制算法，但均流效果良好，能够保证各DG安全稳定运行。

2.2 均流控制算法

基于以上分析，本文提出一种电流直接前馈均流控制算法，其控制框图如图5所示，图中H（s）为系统的闭环传递函数，Z（s）为逆变器等效输出阻抗，mdv、nqv为电流前馈系数，且系数为正。

该均流算法的控制机理如图6所示，则有功功率和无功功率的表达式为

采用虚拟电网磁链定向矢量控制，因此，电压矢量主要定向在q轴上。

假设某一时刻DG2输出有功功率P2大于DG1输出有功功率P1，P2＞P1，而幅值差一般都很小，近似看作是uoq2≈uoq1=-Uon。为了简化分析忽略d轴上的小电压，有功功率 P＝uoqioq，可得|ioq2|＞|ioq1|，施加控制则输出电压幅值减小为Uom2和Uom1，且满足 Uom2＜Uom1，即输出有功大的逆变器 2 的输出电压幅值减小的多，而输出有功功率小的逆变器1的输出电压幅值减小的少，从而实现有功功率均衡分配，如图6（a）所示。

假设某一时刻DG2输出无功功率Q2大于DG1输出无功功率Q1，即Q2＞Q1，同时为了简化分析过程假设该时刻uod2≈uod1=0，则无功功率可以简化为Q=uoqiod，因此，可得|iod2|＞|iod1|，那么施加控制后，输出的d轴电压幅值增大，且满足uod1＜uod2。从图6（b）可得其输出电压矢量分别为Uo2和Uo1，且此时其相角向超前方向变化的相角度满足△φ2＞△φ1，即输出无功功率大的逆变器2输出电压相角度向超前方向变化的多，输出无功功率小的逆变器1相角度向超前方向变化的少，从而缩短两者之间的差距，实现无功功率趋于均衡，如图6（b）所示。

图5 电流直接前馈均流控制框图Fig.5 Block diagram of current direct feed-forward based current sharing control

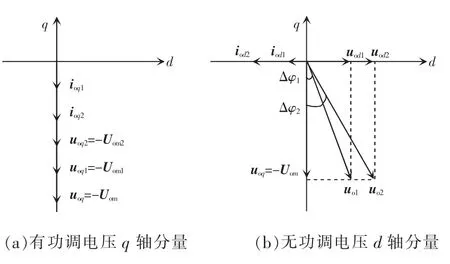
图6 微电网逆变器均流控制机理相量图Fig.6 Phasor diagrams of current sharing control mechanism for microgrid inverter

3 谐波均流分析

通过控制加入的虚拟阻抗可保证低频段呈感性、高频段呈阻性[13]，以方便采取传统下垂控制算法的同时保证非线性负载的均分度与电压供电质量，避免在谐波频段因电感性线路阻抗随信号频率的增大而增大所导致的电压畸变问题[14-17]。

但本文认为，虚拟阻抗与实际阻抗的区别在于它不会随着流过的电流频率的变化而变化，是一固定的虚拟值。所以，没有必要将电流信号的基波与谐波分离后再分别加以虚拟阻抗；同时，前面已经提到，微电网逆变器供电系统区别于逆变器并联供电系统的最大特点就是线路阻抗不为0，且不对称是常态，流过此线路阻抗的基波电流与谐波电流同时受其影响，程度相当，故必然需要加入同样的控制以求基波功率与谐波功率同时得以均分。

3.1 带滤波器的虚拟阻抗理论

图7所示为带滤波器虚拟阻抗纯电阻理论等效示意图，结合本文的均流控制算法，均流控制有两种：低通滤波器式谐波均流控制和低通加带通滤波器式谐波均流控制。

3.1.1 低通滤波器式谐波均流控制

图8为低通滤波器式谐波均流控制框图，加入低通滤波器式虚拟阻抗后，电压参考值为

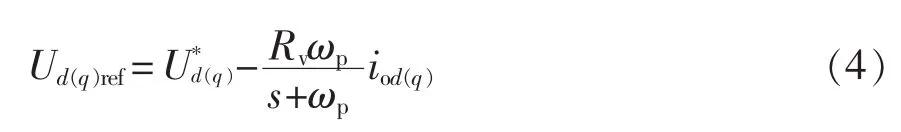
将式（4）代入图2所示的逆变器控制框图，可得系统输入、输出控制关系为

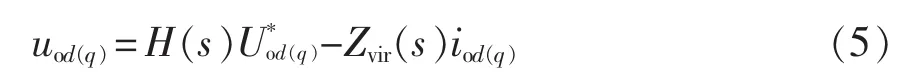
式中，Zvir（s）为等效虚拟阻抗传递函数。

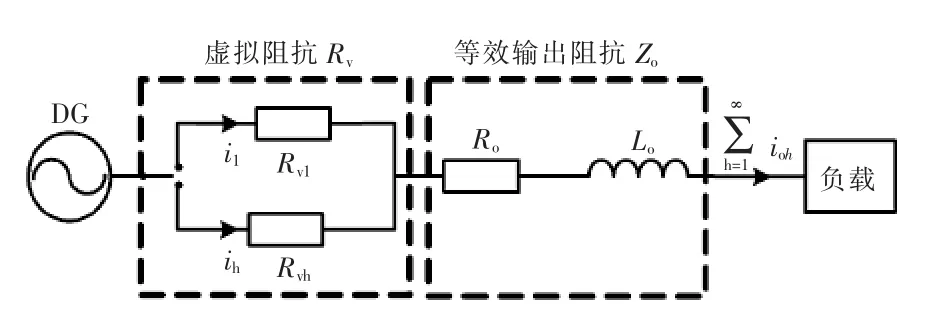
图7 带滤波器虚拟阻抗理论等效示意Fig.7 Equivalent schematic diagram of virtual impedance theory with filter

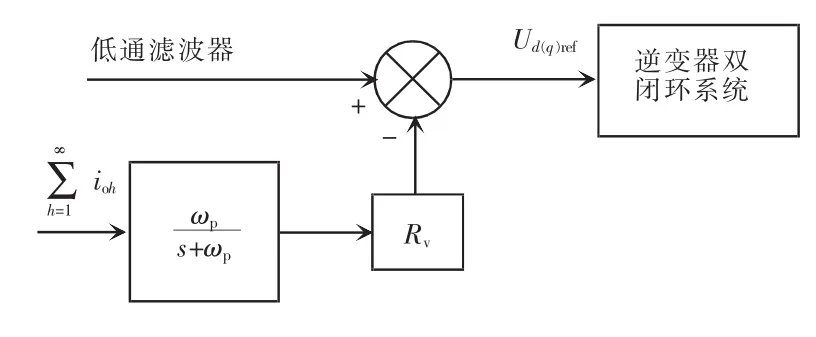
图8 低通滤波器式谐波均流控制框图Fig.8 Block diagram of low-pass filter harmonic current-sharing control

低通滤波器式均流控制的等效输出阻抗为

3.1.2 低通加带通滤波器式谐波均流控制

图9为低通加带通滤波器式谐波均流控制框图，加入低通加带通滤波器式虚拟阻抗之后，电压参考为

将式（7）代入图2所示的逆变器控制框图，可得系统输入、输出控制关系与式（5）相同，只是等效虚拟阻抗不同。低通加带通滤波器式均流控制的等效输出阻抗为

3.1.3 2种均流控制方法输出阻抗对比分析

由式（5）、式（6）和式（8）可以看出：均流控制参数并不影响系统的开环增益函数，因此系统的闭环极点不会发生改变，故不会影响单台逆变器的稳定性、动态性能；均流控制参数对系统的等效输出阻抗有明显影响，故系统的抗干扰能力会发生改变。

因此，本文从等效输出阻抗入手，分析均流控制参数大小对系统抗干扰能力的影响，为控制参数选择提供参考。对这两种谐波均流控制算法的系统等效输出阻抗的bode图进行对比分析，其仿真结果分别如图10和图11所示。

图9 低通加带通滤波器式谐波均流控制框图Fig.9 Block diagram of low pass-band pass filter harmonic current-sharing control

图10 低通滤波器式谐波均流控制的输出阻抗bode图Fig.10 Output impedance bode plots of harmonic current sharing control with low-pass filter

由图10可以看出，转折频率ωp较大时，谐波频次处的阻抗增益也较大，有利于均流；转折频率太小，谐波频段的阻抗值会进一步减小，与均流控制要求恰好相反，此时谐波功率的均分无法保证。所以，如果单纯采用低通滤波器来实现谐波功率的均分，则ωp应该以需要补偿的谐波频率为界，为了保证谐波功率的均分，必须保证该频率量通过，不能对其进行衰减，否则其阻抗值更小，与均流目标相悖。

由图11可以看出，与图10（a）所示的方法比较，低通加带通滤波器式谐波均流控制方法也只是在谐振频率处的幅值特性不同，低频及高频段的频率特性几乎一致。但其有一个优势，即可以实现基波虚拟电阻与谐波虚拟电阻取不同值的控制，如图11（b）所示，其中基波虚拟电阻是谐波虚拟电阻的10倍。

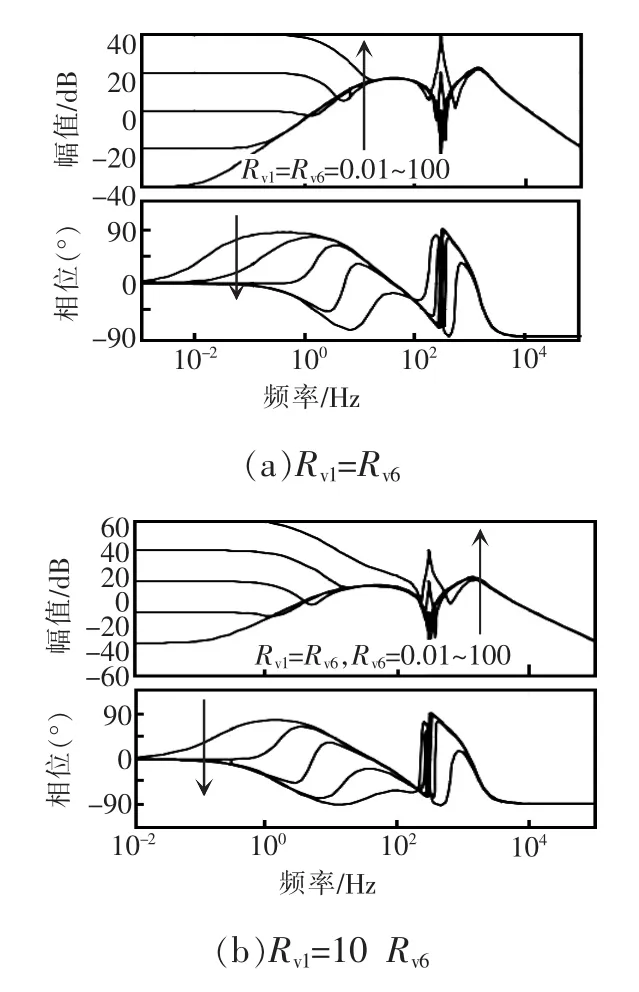
图11 低通和带通滤波器式谐波均流控制输出阻抗bode图Fig.11 Output impedance bode plots of harmonic current sharing control with low-pass and band-pass filter

3.2 无滤波器的虚拟阻抗理论

图12所示为本文所提出的虚拟阻抗纯电阻理论等效示意和控制框图，此方案中没有对负载电流施加滤波器。

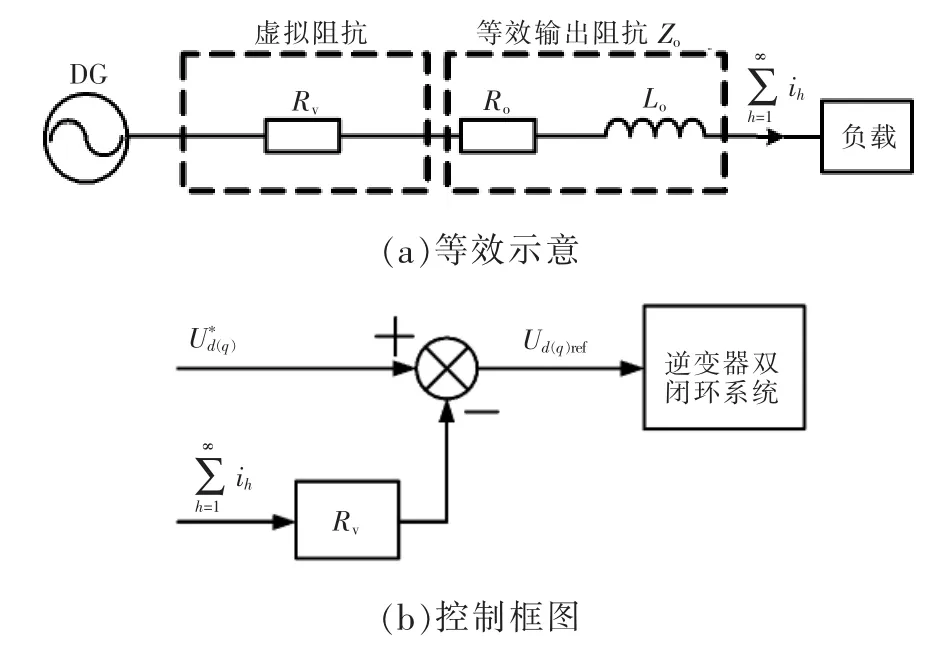
图12 无滤波器的虚拟阻抗理论Fig.12 Virtual impedance theory without filter

应用图12所示的虚拟阻抗理论，再结合本文的均流控制算法，可以得到实现方法为

该控制算法即前面提到的电流直接前馈式均流算法，这只是从虚拟阻抗角度的另一种描述。所以，此处的分析也适用于线性负载的均流。

将式（9）所示的参考电压代入图2所示的逆变器控制框图，可得系统的输出电压控制方程为

等效输出阻抗如式（11）所示。

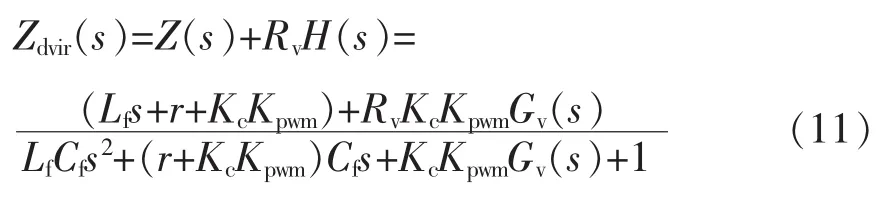
Rv变化时的输出阻抗bode图如图13所示。从图13可以看出，Rv对整个系统高频段的等效阻抗影响不是很大，仍然保有系统对高频干扰信号的衰减作用；Rv主要是对低频段的等效阻抗幅值及相角产生影响，随着Rv的增大，系统低频段的等效阻抗幅值呈比例增大，且低频呈阻性的频段增宽。

另外，单台逆变器设计时提到，R控制器仅在谐振频率处起作用，目的是使谐振频率处的等效输出阻抗接近0，从而抑制负载电流中的谐波分量对逆变器输出电压的影响，保证输出电压的正弦度。但由图13可以看到，随着Rv的增大，R控制器的这一特性逐渐削弱。那么，逆变器输出电压必将因负载电流的谐波分量而发生畸变。因此，Rv不能取得过大，必须在均流精度与电压质量之间折中取舍，本文中 Rv=1 Ω。

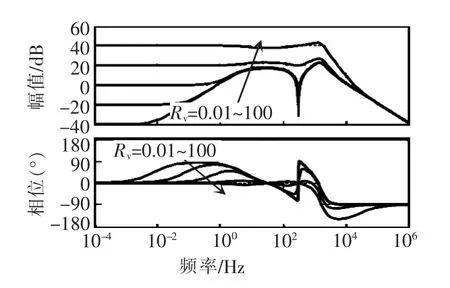
图13 无滤波器式谐波均流控制的输出阻抗bode图Fig.13 Output impedance bode plots of harmonic current sharing control without filter

4 仿真分析

设置两台DG的线路阻抗分别为Rl1=0.16 Ω，Ll1=0.07 mH，Rl2=0.8 Ω，Ll2=0.03 mH。逆变器额定容量为PN=2 000 W，QN=200 var，负载为三相不控整流桥，滤波电容 C=470 μF，负载电阻 R=100 Ω。 逆变器 PR 控制器的参数为 KP=0.1，Ki=10，Kr=50，ωc=5 rad/s。

图14所示为低通滤波器式谐波均流控制下的仿真波形，图15所示为低通加带通滤波器式谐波均流控制下的仿真波形，图16所示为电流直接前馈谐波均流控制下的仿真波形。

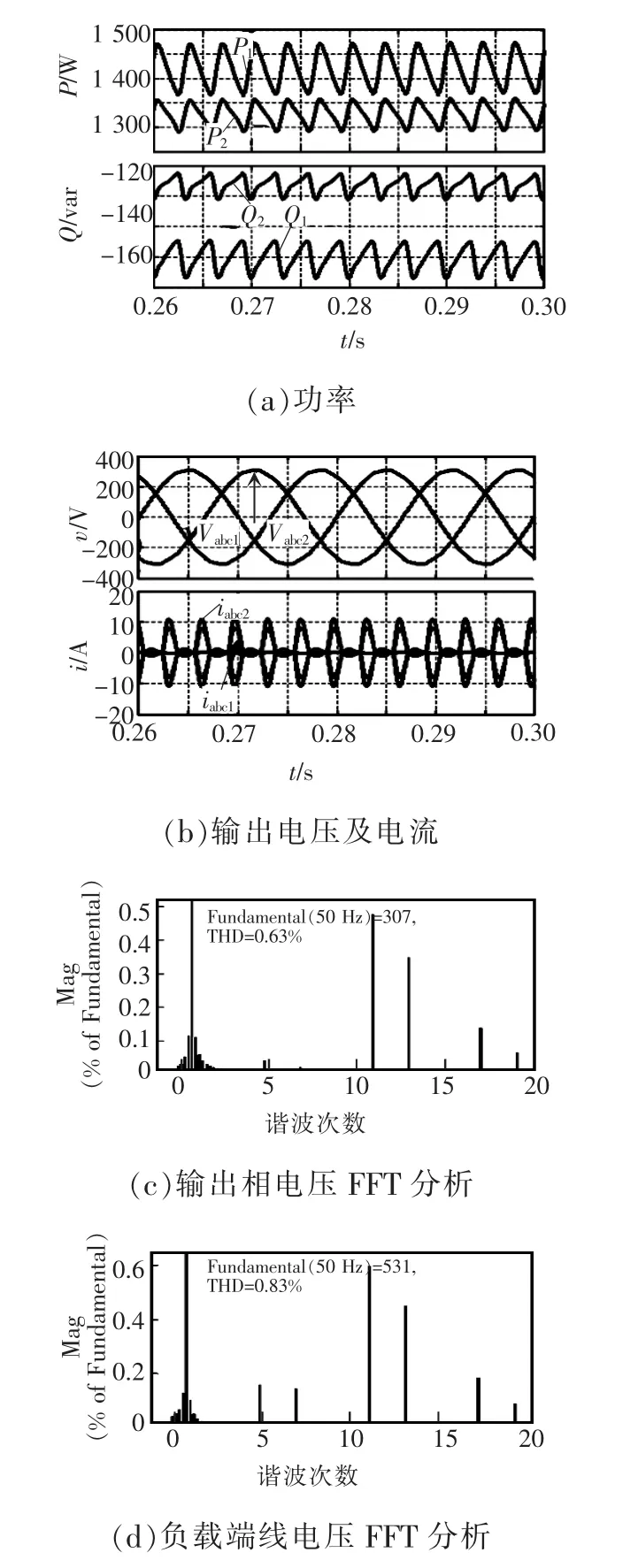
图14 加入低通滤波器式谐波均流仿真波形Fig.14 Simulation waveforms of harmonic current sharing control with low-pass filter（Rv=1Ω，ωp=10rad/s）

仿真波形中有功和无功功率的脉动现象是因为，虽然功率输出加入了低通滤波器，但也只是对谐波功率起到衰减作用，并不能完全消除谐波电流消耗的谐波功率在稳态有功和无功上的体现。本文也是以此来分析谐波功率均分度，不需要额外计算谐波功率。

从图14（a）可以看出，此时2台逆变器的有功功率分别为1 425 W、1 320 W，有功差额为105 W，平均功率约为1 372 W，有功功率峰峰值为100 W、60 W；无功功率分别为-150 var、-125 var，无功差额为25 var，平均无功功率为-137 var，无功功率峰峰值为12 var、9 var。由此，加入低通滤波器后的确可以使供电电压波形质量有所改善，但基波与谐波功率均分度都较差。从图14（b）可以看出，均流效果较差。同时，从图14（c）和 （d）中可以看出，逆变器输出相电压和负载端线电压的电压总畸变率分别为0.63%、0.83%，波形质量良好。

将图15与图14进行对比可以看出，加入带通滤波器提取谐波而后额外加入虚拟电阻的方法，其谐波均流效果得到明显改善；同时，电压质量有所降低，输出相电压及负载端线电压的总谐波畸变率分别由0.63%、0.83%上升到0.74%、0.86%，而且进一步增加了控制实现的难度。

图15 加入低通和带通滤波器的谐波均流仿真波形Fig.15 Simulation waveforms of harmonic current sharing control with low-pass and band-pass filter（Rv1=1Ω，Rv6=0.2Ω）

图16 电流直接前馈式谐波均流仿真波形Fig.16 Simulation waveforms of harmonic current sharing control with current direct feed-forward

从图16（a）的功率仿真波形可以看出，此时两台逆变器输出的有功功率分别为1 385 W、1 300 W，峰峰值均为80 W，有功功率差额为85 W，平均有功功率约为1 343 W；无功功率分别为－107 var、－126 var，峰峰值约为 10 var、10 var，平均无功为－116 var，无功差额为 19 var。 从图16（b）中逆变器A相电流仿真波形也可以看出，两台逆变器的输出电流基本重合，环流很小。由此可见，系统基波功率均分度良好，系统的谐波均流效果也良好。从图16（c）和（d）中可以看出，逆变器相电压和负载端线电压的电压总畸变率分别为1.24%、1.42%，与图14和图15所对应的均流算法相比，电能质量有所降低。但相差不大，满足电网标准要求的5%。

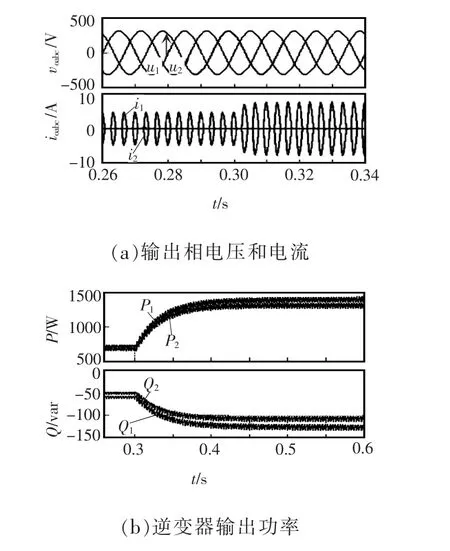
图17 电流直接前馈谐波均流动态波形Fig.17 Current direct feedforward harmonic currentsharing dynamicswaveform

为了进一步验证电流直接前馈均流的动态谐波均流能力，本文进行了半载到满载的仿真，逆变器输出电压电流及功率波形如图17所示，仿真结果可以看出，本文所选谐波均流算法动态均流能力较好，电能质量也满足小于5%的要求。

5 结语

本文通过定性分析证明了线路阻抗不平衡是微电网逆变器均流控制的关键难题；线路阻抗不平衡时，若要实现并联系统均流，则各台DGs的输出电压必然不相等。本文跳出电压频率和幅值下垂的固有思路，提出了一种电流直接前馈均流控制算法，该算法不以频率为受控量，故而可以保证系统频率恒为50 Hz，有利于提升系统供电的稳定性。同时，该算法对于线路阻抗不平衡是常态的微电网逆变器并联系统具备良好的基波与谐波均流效果。与以往加入低通滤波器或者带通滤波器的谐波均分控制算法相比，基波功率和谐波功率的均流效果相当，但此算法控制实现简单，环路大为减少，所以系统可靠性提高。

[1]Chen Min,Zheng Chongfeng,Qian Zhaoming,et al.The analysis of the inverter under rectifier load using a nonlinear rectifier model[C].INTELEC05,2005:453-458.

[2]Chen Min,Qian Zhaoming,Yuan Xiaoming.The analysis of the characteristics of the inverter with rectifier load using a nonlinear rectifier model[C].PESC06,2006:1-16.

[3]陈敏.非线性负载条件下的逆变器特性研究[D].杭州:浙江大学,2006.

[4]张新亮,陈照章,徐晓斌.基于电流分解的逆变器无连线并联控制[J].电子技术应用,2008，34（12）:75-78.Zhang Xinliang,Chen Zhaozhang,Xu Xiaobin.Wireless and parallel operation control technology of inverter based on current decomposition[J].Power Supply Technology and Its Application,2008,34（12）:75-78（in Chinese）

[5]周念成,池源,王强钢.含非线性及不平衡负荷的微电网控制策略[J].电力系统自动化,2011,35（9）:61-66.Zhou Niancheng,Chi Yuan,Wang Qianggang.Control Strategies for microgrid containing non-linear and unbalanced loads[J].Automation of Electric Power Systems,2011,35（9）:61-66（in Chinese）.

[6]Shahnia F,Majumder R,Ghosh A,et al.Operation and control of a hybrid microgrid containing unbalanced and nonlinear loads[J].Electric Power Systems Research,2010（808） :954-965.

[7]Savaghebi1 M,Guerrero M,Jalilian1 A,et al.Hierarchical control scheme for voltage harmonics compensation in an islanded droop-controlled microgrid[C].Proceedings of the International Conference on Power Electronics and Drive Systems,2011,（2）:89-94.

[8]陈宏志,王旭,刘建昌,等.基于阻抗匹配模式的并联逆变器均流方法[J].电机与控制学报,2012,16（8）:36-41.Chen Hongzhi,Wang Xu,Liu Jianchang,et al.Current sharing method for parallel inverters based on impedance matching mode[J].Electric Machines and Control,2012,16（8）:36-41（in Chinese）.

[9]马添翼,金新民,梁建钢.孤岛模式微电网变流器的复合式虚拟阻抗控制策略[J].电工技术学报,2013,28（12）:304-312.Ma Tianyi,Jin Xinmin,Liang Jiangang.Multiple Virtual Impedance Control Method of Microgrid Converter under Island Mode[J].Transactions of China Electrotechnical Society,2013,28（12）:304-312（in Chinese）.

[10]Jos'e M,Miguel C,Luis G de V,et al.Virtual impedance loop for droop-controlled single-phase parallel inverters using a second-order general-integrator scheme[J].IEEE Transactions on Power Electronics,2010,25（12）:2993-3002.

[11]王君瑞,吉炫玮,张晋宁,等.双馈风力发电系统空载比例谐振并网控制[J].电力电子技术,2017,51（4）:43-45.Wang Junrui,Ji Xuanwei,Zhang Jinning,et al.idle load proportional resonant grid connection control for doubly-fed wind power generation system[J].Power Electronics,2017,51（4）:43-45（in Chinese）.

[12]张纯江,王晓寰,薛海芬,等.微网中三相逆变器类功率下垂控制和并联系统小信号建模与分析[J].电工技术学报,2012,27（1）:32-39.Zhang Chunjiang,Wang Xiaohuan,XueHaifen,et al.A quasi-power droop control of three-phase inverters and small signal modeling and analysis of parallel system in micro-grid[J].Transactions of China Electrotechnical Society,2012,27（1）:32-39（in Chinese）.

[13]程军照,李澍森,吴在军,等.微电网下垂控制中虚拟电抗的功率解耦机理分析[J].电力系统自动化,2012,36（7）:27-32.Cheng Junzhao,Li Pengsen,Wu Zaijun,et al.Analysis of power decoupling mechanism for droop control with virtual inductance in a microgrid[J].Automation of Electric Power Systems,2012,36（7）:27-32（in Chinese）.

[14]Huang Wangxin,Jaber A A Q.Energy sharing control scheme for state-of-charge balancing of distributed battery energy storage system[J].IEEE Trans on Industrial Electronics,2015,62（5）:2764-2776.

[15]Qobad S,Josep M G,Juan C V.Distributed secondary control for islanded microgrids—A novel approach[J].IEEE Transactions on Power Electronics,2015,29（2）:1018-1031.

[16]孙孝峰,秘晓梦.微电网分布式发电逆变器下垂控制综述[J].燕山大学学报,2016,40（3）:189-201.Sun Xiaofeng,Bi Xiaomeng.Overview of droop control of distribution generation inverters in microgrid[J].Journal of Yanshan University,2016,40（3）:189-201（in Chinese）.

[17]王逸超,罗安,金国彬,等.大连线阻抗环境下的微网逆变器并联运行策略[J].中国电机工程学报,2015,35（4）:858-865.Wang Yichao,Luo An,Jin Guobin,et al.Microgrid inverter parallel operation strategy in large feeder impedance environment[J].Proceedings of the CSEE,2015,35（4）:858-865（in Chinese）.

张纯江

张纯江（1961－），男，中国电源学会高级会员，通信作者，博士，教授，博士生导师，研究方向：电力电子功率变换及控制、光伏风力变流器及并网控制、微电网及储能系统功率流控制，E-mail：zhangcj@ysu.edu.cn。

郭忠南（1980－），男，博士研究生，讲师，研究方向：电力电子功率变换与控制、新能源并网发电技术，E-mail：gzn1216@ysu.edu.cn。

郭吉平(1962-)，女，本科，教授，研究方向：计算机控制技术，E-mail:jipingguo@jmsu.edu.cn。

张丽(1989-)，女，硕士研究生，研究方向：微电网逆变器控制，E-mail:1442522149@qq.com。

王晓寰(1980-)，女，博士，副教授，研究方向：光伏并网逆变器控制、孤岛检测技术，E-mail:wxh@ysu.edu.cn。

Harmonic Current-sharing Control of Inverters in Autonomous Microgrid of Photovoltaic Power Generation

ZHANG Chunjiang1,GUO Zhongnan1,GUO Jiping2,ZHANG Li1,WANG Xiaohuan1
（1.School of Electrical Engineering,Yanshan University,Qinhuangdao 066004,China;2.School of Electric Information,Jiamusi University,Jiamusi 154007,China）

Firstly,the power transfer characteristic of the interface inverters applied to microgrid was qualitatively analyzed this paper,proving that the unbalance of line impedance is the key problem of the current-sharing control of micro-grid inverters.Then,a simple and feasible direct current feedforward current-sharing control strategy is proposed whic can not only eliminate the calculations of the active power,reactive power,and the voltage synthesis in conventional droop control,but also fix frequency at 50 Hz while achieving the current balance between the parallel inverters.In addition,the effect of virtual impedance on current-sharing was analyzed in detail and a harmonic currentsharing control was proposed without a filter.The contrast analysis was done to the proposed sharing control strategy and the harmonic current-sharing methods with a filter in detail.Finally,the simulation results in Matlab/Simulink verify the rationality and effectiveness of the proposed control.

autonomous microgrid;interface inverter;harmonic current-sharing;virtual impedance

10.13234/j.issn.2095-2805.2017.6.26

TM464

A

2017-07-31；

2017-11-27

国家自然科学基金资助项目（51607154）

Project Supported by National Natural Science Foundation of China（51607154）