液压驱动冗余并联机构内力分析及抑制
高长虹,杨志东,丛大成,韩俊伟,杨炽夫
(哈尔滨工业大学 机电工程学院,黑龙江 哈尔滨,150001)
液压驱动冗余并联机构内力分析及抑制
高长虹,杨志东,丛大成,韩俊伟,杨炽夫
(哈尔滨工业大学 机电工程学院,黑龙江 哈尔滨,150001)
针对液压驱动冗余并联机构内力问题,分析内力空间及其基的构成,在自由度控制框架下研究不同因素对系统内力的影响。提出基于误差最小控制综合算法(Er−MCSI)的内力抑制策略,以克服液压系统中较强的时变非线性和干扰因素对内力抑制效果的影响。以1个具有2个冗余自由度的六自由度液压驱动冗余并联机构为例,仿真研究该机构分别在等位移、等速和等加速度段工况下不同因素对系统内力的影响,并对其进行内力抑制。研究结果表明:提出的内力抑制策略可实现内力抑制增益在线自适应调节,具有较好的内力抑制效果。
液压驱动;冗余并联机构;内力抑制;最小控制综合
液压驱动并联机构通常具有刚度大、精度高、承载能力强等优点。此外,并联机构可以通过增加冗余驱动形式达到消除机构奇异、优化关节驱动力、提高系统出力的目的,因此,液压驱动冗余并联机构已被广泛用来作为各种运动模拟、振动环境测试及力加载设备[1−3]。然而,在冗余驱动的情况下,机构通常会因为驱动系统特性不一致、伺服阀零漂和传感器测量误差等因素,产生较大的内力。这种内力对外不作功,但减小了系统的净出力,严重时会破坏机构,导致系统无法正常工作[4−5]。很多学者对电动冗余并联机构的运动控制及内力抑制进行了研究。由于伺服电机易于实现力矩控制,在基于模型的控制框架下,通过优化和控制各驱动器的力矩输出可使机构具有良好的动态性能[6]。然而,液压系统通常具有较强的非线性和小阻尼特性,液压缸不易作为一个理想的“力发生器”,基于模型的控制策略难以应用[7−8]。在冗余结构下,各液压缸独立的位置控制容易使系统产生较大的内力。目前,在关于液压驱动冗余并联机构内力抑制的文献中,内力抑制策略多是以系统在小范围(运动范围远小于台体尺寸[9])内运动进而可采用零位线性化方法的假设前提下提出的,如关广丰等[10]提出的压力镇定控制技术、UNDERWOOD等[11]提出的八自由度控制策略等。PLUMMER[9]总结了此类机构的特点,提出在工作自由度空间采用零位线性化的自由度控制,在冗余自由度空间采用力控制的策略保证机构在运动过程中存在的内力较小。然而,冗余并联机构的内力形态通常随着机构的位姿改变而改变,特别是当系统的运动范围较大时,内力会表现出较强的时变性且其幅值波动较大,基于零位线性化下的假设将无法真实反映机构的运动状态和存在的内力情况。针对一类由液压驱动、具有冗余并联结构形式的机构内力问题,本文作者通过分析内力空间及其基构成,在自由度控制结构框架下研究不同因素对系统内力的影响。在对冗余自由度进行力控制的基础上,提出基于误差最小控制综合算法(Er−MCSI)的内力抑制策略,以克服液压系统中较强的时变非线性和干扰因素对内力抑制效果的影响。最后以1个具有2个冗余自由度的六自由度液压驱动冗余并联机构为例,对先前理论分析和提出的控制策略进行仿真验证。
1 内力特性分析
液压驱动冗余并联机构属于静不定系统,在正常工作时通常会由于系统内部或外界的因素产生较大的内力,因此,研究不同因素对系统内力的影响对分析系统内力特性及设计内力抑制控制器尤为重要。
1.1 内力空间及其基构建
冗余并联机构动力学模型可以简化表达成如下形式[12]:
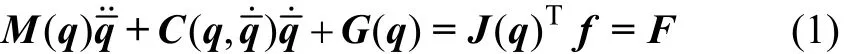
式中: f ∈ Ri为液压缸出力,i为驱动器数目;F ∈Rj表示自由度空间广义力,j为机构自由度数;M(q ) ∈ Rj×j,C(q,q˙)∈ Rj×j和 G (q ) ∈ Rj分别为惯性坐标系下的质量矩阵、离心力及科氏力系数矩阵、重力项;分别表示平台位姿、自由度空间广义速度和广义加速度;J(q ) ∈Ri×j为速度雅克比矩阵。
将液压缸出力作为未知变量,则式(1)中变量数多于方程数,该方程组是欠定方程组,其通解形式为

式中: ( JT)+∈Ri×j为JT的伪逆矩阵;I ∈ Ri×i为单位阵; λ ∈ Ri,理论上可以任意取值,为了便于分析,与实际物理模型相对应,选取λ=f。
由式(2)可以看出: f由2部分组成, ( JT)+F为式(1)的特解, [ I - (JT)+JT]f为齐次线性方程组J(q )Tf=0的通解。因此,只有特解部分对外作功,用来抵抗外载和维持系统运动,通解部分不对外作功,实为冗余并联机构的内力。
用S表示内力空间,令 B = I - (JT)+JT为内力空间矩阵,则S与f存在如下的映射关系:

则内力空间内的任意元素 s ∈ Ri都应满足
内力空间的维数dimS = r ank(B ) = i- j ,则可将内力空间S表示为

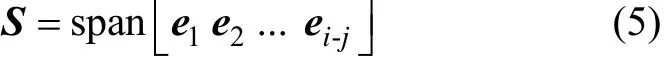
式中:span为向量的线性组合;[ e1e2... ei-j]为矩阵B的(i−j)个线性无关的列向量,可以看作S的一组基底。若将内力空间基底用E ∈ Ri×(i-j)来表示,则空间基底可通过 n ull(JT)求出,null为MATLAB零空间求解命令。

式中: F ∈Ri-j为(i−j)个冗余自由度空间的力组成的力向量。
1.2 内力的影响因素
液压驱动冗余并联机构实为一个复杂的时变非线性系统,为了便于分析不同因素对系统内力的影响,将系统进行线性化处理。为了避免独立的单缸位置控制给系统带来较大的内力,通常此类机构采用自由度控制方式。图1所示为自由度控制框架结构。图1中虚线左边为控制部分,右边为实际物理对象。qc,qf,分别表示给定位姿、实际反馈位姿和位姿误表示冗余自由度广义速度;i,ir,lf∈Ri分别表示液压缸速度,冗余速度和位移传感器测量值;分别表示冗余自由度质量矩阵、阻尼矩阵和刚度矩阵;分别为控制器、自由度分解矩阵;FKM(P,lf)为运动学正解,是关于结构参数P和位移传感器测量值lf的函数;为伺服阀环节;A, G ∈Ri×i分别为液压qp缸的有效作用面积及其动态部分。
冗余并联机构驱动形式的不同,导致其内力产生的因素也有所不同。对于液压驱动类型的冗余并联机构来说,影响内力的因素能够被归纳以下3类:驱动系统特性不一致、伺服阀零漂和传感器测量误差。如图1所示,将各驱动系统特性表现的不一致性用矩阵表示,特性一致时该矩阵为单位阵。u ∈Riz为引进的伺服阀零漂。参与控制的实际反馈位姿 qf由包含传感器测量误差 lm∈ Ri的各作动器位移 lf和结构参数P通过运动学正解求得。
1.2.1 驱动系统特性不一致性
驱动系统特性不一致性表现为各液压缸有效面积、腔室容积、泄漏系数、负载特性等参数不一致,各伺服阀固有频率、阻尼比、放大器增益等参数不一致。设 Gˆ ( s)表示阀控缸驱动系统特性完全一致的部分模型,ΔG(s)为模型偏差,表示系统特性不一致的部分,则实际系统的传递函数可表述为Gˆ(1+ΔG)。将特性不一致性用矩阵 Kd表示,令 Kd(s) = 1 + ΔG ( s ),如图1所示。此时认为 uz与 lm的干扰为0,则

在无传感器测量误差及结构参数误差时,自由度分解矩阵cJ等于真实的雅克比矩阵J。冗余自由度刚度一般较大,式(9)中q˙r引起的内力部分可近似忽略。根据性质 ETJ =0,可将式(8)和式(9)转换为:

由式(12)可知稳态时位姿误差通常由干扰力如重力产生,为了抵抗外界干扰伺服阀口通常为小开口状态。由式(13)可知此时驱动特性不一致因素的存在会导致系统内力的产生。
1.2.2 伺服阀零点漂移
伺服阀因供油压力和工作温度的变化会引起伺服阀零点漂移,如图1所示,引入时变量 uz(t)表示伺服阀零点漂移,此时认为动态特性矩阵Kd为单位阵和传感器测量误差lm为0,则

根据下式可求得稳态时系统的位姿误差eq和内力rF:
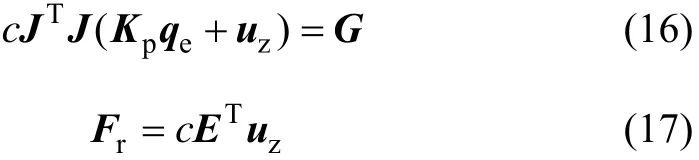
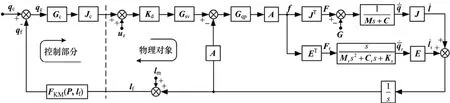
图1 液压驱动冗余并联机构自由度控制Fig. 1 Degree-of-freedom (DOF) control of hydraulically driven redundant parallel mechanism (HDRPM)
由式(15)和式(17)可知:当存在伺服阀零点漂移时,系统内力受到内力空间基底变化和零点漂移的影响。
1.2.3 传感器测量误差
当系统存在传感器测量误差时,设计的自由度分解矩阵cf( )J q 并不等于真实的雅克比矩阵 ()Jq。此时,认为动态特性矩阵Kd为单位阵和伺服阀零点漂移uz为0,则


由式(19)和式(21)可知,此时系统内力与系统控制量peKq成正比。
此外,平台和球铰的机械加工和安装误差会造成机构的名义结构参数值偏离真实的结构参数值,运动学正解评估的位姿不准确,这部分因素可以和传感器测量误差归为同一类。一般情况下,以上3种因素会同时存在于系统中,此时,

稳态时系统的内力Fr为
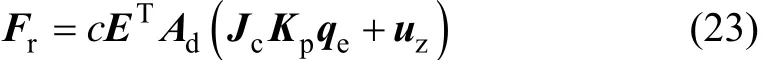
由式(22)和式(23)可见:此时系统的内力为3种因素影响下的内力部分叠加,参数变量Kd,Jc和uz影响了系统内力。
2 内力抑制
结合先前对内力特性的分析,提出如图2所示的控制策略,主要包含自由度位姿控制和基于Er−MCSI算法的内力抑制部分。
基于运动学正反解的自由度位姿控制根据测量的液压缸位移及机构的结构参数经正解解算求得平台当前的位姿,与位姿给定指令qc比较得到的位姿误差经过“比例+积分+滞后(PIL)控制器”后由计算的雅克比矩阵Jc转换成伺服阀驱动信号up。
冗余自由度的内力通常直接施加到运动平台,而加工平台的机械刚度一般较大,故在冗余自由度空间进行力控制比较合适。然而,当采用线性控制器在某个工作点调整内力抑制增益使系统内力较小时,工作点改变、液压系统时变非线性及干扰因素均会影响内力抑制效果,甚至造成系统不稳定。为了克服这个缺点,内力抑制控制器采用基于Er−MCSI算法的控制。
最小控制综合(MCS)算法是对基于Popov超稳定理论的参考模型自适应(MRAC)的发展和延伸,基本保留了MRAC的所有优点,而且自身具有多个优点:MCS算法不需要进行模型辨识,不需要设计线性控制器,对于具有时变参数、内部动态耦合及外界干扰的非线性系统具有良好的控制性能,该算法已被证明具有很好的稳定性和鲁棒性,并成功应用于多个领域[13−15]。Er−MCSI是 MCS算法的 1种改进算法,该算法只把信号误差作为驱动源,且增加显式积分项,解决了由于系统工作点位置变化造成 MCS算法增益难以快速调整及外界干扰和偏置信号引起的增益饱和问题[16]。Er−MCSI算法原理如图3所示。

图2 液压驱动冗余并联机构内力抑制策略Fig. 2 Internal force rejection strategy(IFR) of HDRPM
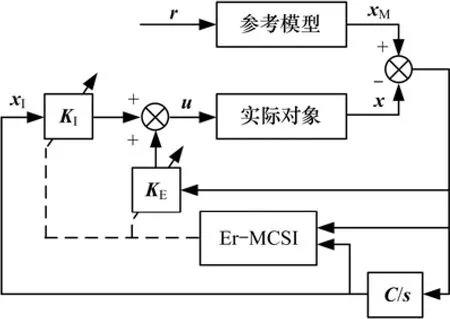
图 3 Er−MCSI算法图Fig. 3 Figure of Er−MCSI algorithm
为了应用Er−MCSI算法,首先应推导液压驱动冗余驱动并联机构冗余自由度内力空间状态方程。设伺服阀阀芯电压控制量uv为输入向量,液压缸出力f为输出向量,并取状态向量:
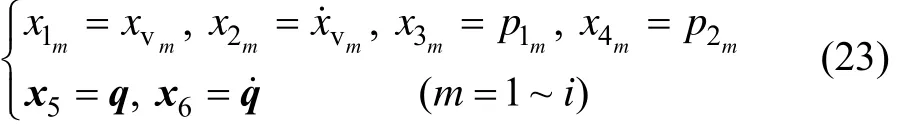
式中:xvm,p1m和p2m分别为第m个伺服阀阀芯位移及液压缸2腔压力。
先不考虑影响内力因素,系统状态空间方程可表述如下:

式中:ωvm,ζvm,kam和kvm分别为第m个伺服阀的固有频率、阻尼比、放大器增益及阀芯位移与电流信号间比例系数; Am, cicm,cecm,V10m和V20m分别为第m个液压缸的有效面积、速度、内泄漏系数、外泄漏系数及2腔各自初始容积;βe为体积弹性模量;fl和 fr为进出液压缸2腔的流量函数;IKM表示由平台当前实际位置反解得到的液压缸位移向量。
将式(24)和式(25)转换成矩阵形式

式中:状态向量 x~ ( t) ∈ R(4i+2j);输入向量 u (t) ∈ Ri;
v输出向量 y~ ( t)∈ Ri;系统矩阵 A~ ( t) ∈ R(4i+2j)×(4i+2j);输入矩阵 B~ ∈ R(4i+2j)×i;输出矩阵 C~ ∈ Ri×(4i+2j);
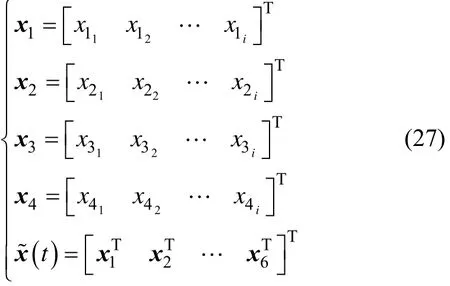
考虑系统存在影响内力的因素,取内力抑制环冗余自由度内力误差控制量为fru,输出向量为自由度内力rF,则

将式(28)代入式(26)可求得最终内力抑制部分状态方程矩阵形式为

式中:状态向量 x ( t) ∈ R(i-j);系统矩阵A ( t) ∈ R(i-j)×(i-j);输入矩阵 B ( t) ∈ R(i-j)×(i-j);干扰向量 d ( t) ∈ R(i-j);输出矩阵C取(i−j)阶单位矩阵。
设线性参考模型状态方程为:
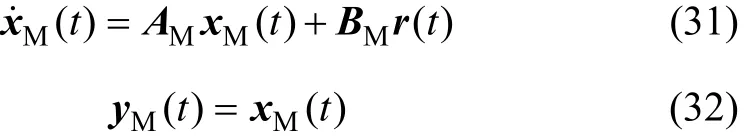
则Er−MCSI算法控制律可表示为
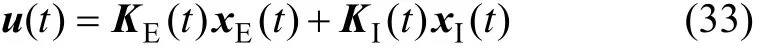
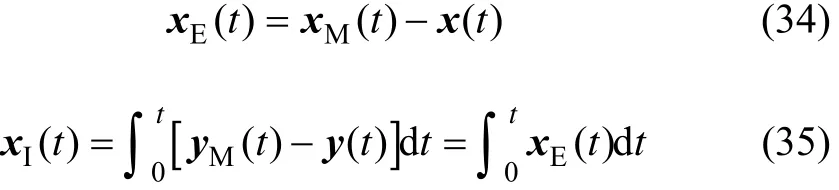
考虑高带宽噪声等未建模动态造成的自适应增益不收敛影响,采用σ−修正法[17]对自适应控制器增益进行修正,以提高系统的稳定性。

式中:P为李亚普诺夫等式解,为正定对称阵;Q为严格正实矩阵;Ce为输出误差矩阵。
故最终在应用基于 Er−MCSI算法的内力抑制策略时,各液压缸出力首先经内力空间基底的转置矩阵ET转换成冗余自由度力 Frf,与给定零力命令 Frc进行比较,经过Er−MCSI算法后计算出控制量,再由基底矩阵Ec转化成各伺服阀输入信号uf,与自由度位姿控制得到的伺服阀输入信号 up合并形成最终伺服阀驱动指令u驱动相应各液压缸运动。
3 案例仿真
3.1 系统描述
以1个具有2个冗余自由度的六自由度液压驱动冗余并联结构为例进行相应的内力分析及抑制。图 4所示为该机构结构图。该机构由8套伺服液压作动器、上平台和基础等组成。台面加工4个角用于安装水平和垂向液压缸上铰支座,每条液压缸与上平台及基础间通过球铰连接。水平两向4条液压缸上下铰点中心连线与平台相应侧边均成 45°。台面长×宽为 1 m×1 m,水平双向最大位移为±0.28 m,垂向最大位移为±0.18 m,运动范围相对较大。
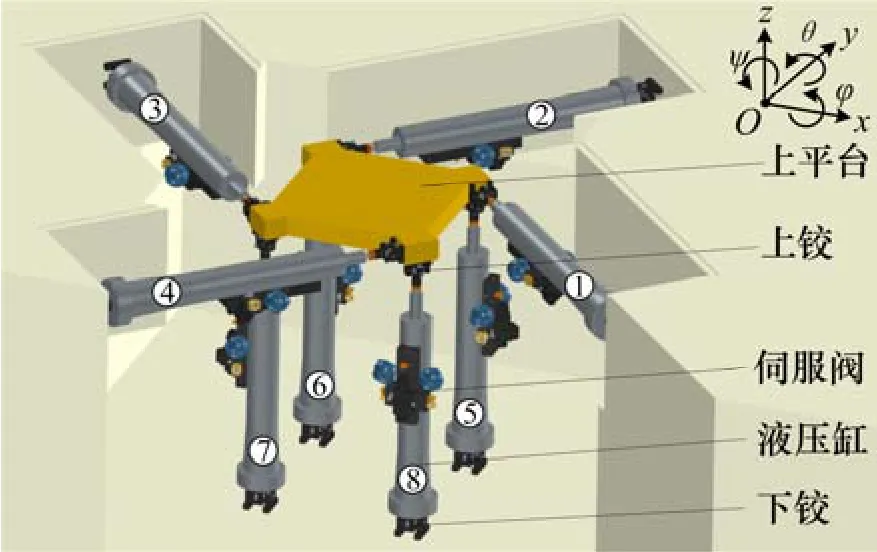
图4 六自由度液压驱动冗余并联机构结构图Fig. 4 Configuration of 6-DOF HDRPM
根据1.1节理论分析,通过内力空间基底的求解,可获得该机构在中位时的内力形态如图5所示。水平面内的1个内力形态为:1号和3号液压缸出力为推力,2号和4号液压缸出力为大小相等的拉力;垂直平面内的1个内力形态为:5号和7号液压缸出力为推力,6号和8号液压缸出力为大小相等的拉力。此内力形态随着平台位姿改变而改变,由式(5)可以方便地分析出冗余并联机构在任一位姿下的内力空间形态。
3.2 不同因素对系统内力的影响
使用ADAMS动力学分析软件建立该机构的机械模型;使用MATLAB/SIMULINK数学建模软件建立非线性液压模型、运动学正反解及控制器模型。通过两者联合仿真最终搭建如图2所示的冗余并联机构控制结构框架,主要仿真参数如表1所示。

图5 液压驱动冗余并联机处于中位时内力形态Fig. 5 Internal force forms of HDRPM in middle position

表1 仿真参数Table 1 Simulation parameters
为了验证1.2节理论分析的正确性,3种因素Kd,uz和lm被加入仿真模型中,并研究其对系统内力的影响。如图6所示,水平x向工作频段取0.5~5.0 Hz,以0.5 Hz为间隔共包含10种正弦运动工况。图6显示的位移幅值放大了20倍,10种工况对应的位移范围为0.056~0.200 m,速度范围为0.628~2.513 m/s,加速度范围为(0.20~5.64)g。其中0.5~2.0 Hz为等位移输入工况,2.0~3.5 Hz为等速度输入工况,3.5~5.0 Hz为等加速度输入工况。仿真时考虑 Kd,uz和 lm这 3种因素仅作用于水平向4条作动器,大小取常值,分别为 diag(0.97 1.03 1.02 0.95 1 1 1 1),[0.03 0 0.03 0 0 0 0 0]TV,[0.003 0 0.001 0.005 0 0 0 0]Tm。图6中Fr−Kd,Fr−uz和Fr−lm分别表示在3种因素影响下2个冗余自由度方向产生的最大内力幅值。为方便比较,图中Fr−uz幅值放大4倍,Fr−lm幅值放大20倍。由图2可知:在仿真模型中内力基底 Ec是由 Jc推导而来,则式(19)和式(22)应分别替换为:

则稳态时仅在lm影响下系统内力Fr为0。
从图6可以看出:在Kd和lm因素影响下的内力变化趋势与机构运动速度大小基本一致,与式(11)和式(43)的理论推导结果一致;仅在uz因素影响下,不同工况的最大内力幅值变化很小,如式(15)仅受到系统内力空间基底Ec变化的影响。此外,在系统零位处仿真得到 3种因素影响下的最大内力稳态值分别为0.6,2.0和0.3 N,这和式(13),(17)及(43)计算的结果基本一致,进一步验证了1.2节理论推导的正确性。
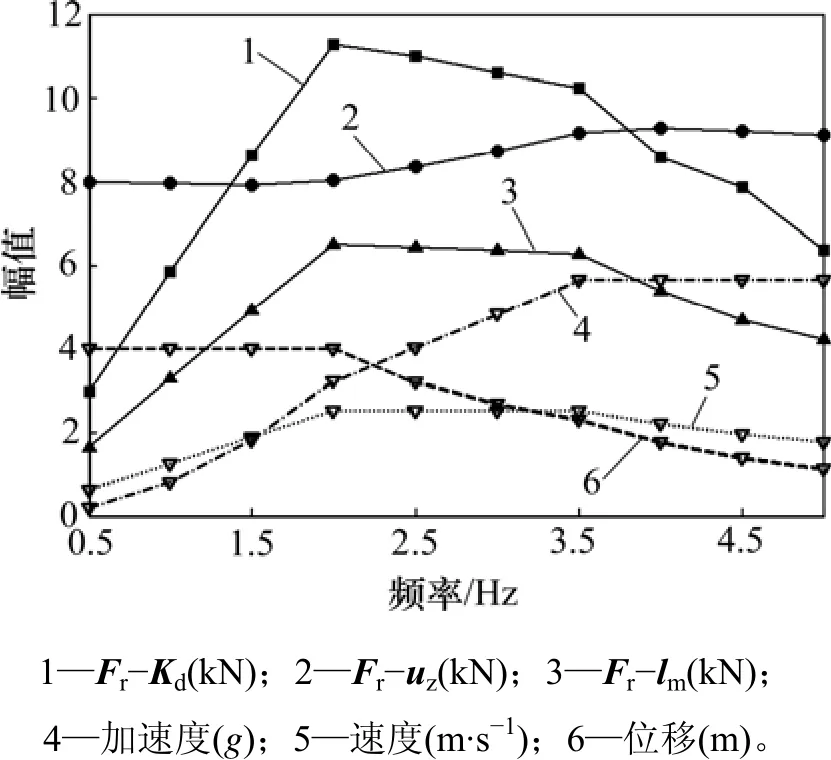
图6 不同工况下不同因素影响产生的内力Fig. 6 Internal forces under different conditions with different factors
3.3 内力抑制仿真
为了考察系统在大范围运动时的内力抑制效果,如图7所示给平台输入水平面内的圆轨迹运动指令:x=0.1sin(4πt ), y =0.1cos(4πt),其他自由度给定为0;运动前1 s为过渡阶段,1 s后进入满幅值工作状态,整个运动时间持续10 s。仿真时前1~4 s加入与3.1节相同取值的Kd,uz和lm影响内力的因素。为了考察提出的内力抑制策略的内力抑制自适应能力,从第 4 s起加大水平向各作动器的不一致性和伺服阀零偏,取Kd= diag(0.92 1.12 1.05 0.9 1 1 1 1),uz= [0.03 −0.02 0.03 −0.02 0 0 0 0]T。此外,自适应参考模型取时间常数为0.01的一阶惯性环节,自适应权值矩阵α和β分别为[2e−100; 0 2e−10]和[2e−110; 0 2e−11],修正因子 σ 为[0.1 0; 0 0.1],输出误差矩阵Ce为[1 0; 0 1]。

图7 运动轨迹跟踪Fig. 7 Motion trajectory tracking
图8 所示为内力抑制仿真结果。从图8可以看出:在未加内力抑制时,4 s前作动器最大内力约占作动器最大出力的10%;4 s后,由于干扰因素幅值加大,作动器内力和出力也随之增大,水平作动器最大出力为15.3 kN,最大内力为4.2 kN,内力约占作动器最大出力的28%,这严重影响了系统的净输出能力。
图 8(c)与图8(d)表明:整个运动阶段水平作动器最大出力为12.0 kN,即使在内力干扰因素幅值加大以后,作动器出力最大幅值基本保持一致。作动器最大内力最终被降低至300 N以内,仅占此时作动器最大出力的2.5%。从内力抑制前后对比来看,作动器最大出力降低了21%,最大内力降低了93%。
由图8(e)与图8(f)可以看出:在第4 s加大干扰因素幅值后,自适应增益根据状态误差量能够较快地进行自适应调整。当内力抑制到某一较小值时自适应增益最终趋于稳定状态。图8(g)所示为图2所示的内力抑制控制量uf的变化情况。由于4 s前内力较小,内力抑制控制量较小。4 s后,随着系统内力增大,由内力抑制算法产生的控制量也随之增大。从整个运动过程来看,提出的内力抑制策略实现内力抑制增益在线自适应调节,具有较好的内力抑制效果。

图8 内力抑制仿真结果Fig. 8 Simulation results under IFR
4 结论
1) 针对一类由液压驱动、具有冗余并联结构形式机构的内力问题,在自由度控制结构框架下研究了液压驱动系统特性不一致、伺服阀零漂和传感器测量误差3种因素对系统内力的影响。在驱动系统特性不一致和传感器测量误差因素影响下,系统内力变化趋势与机构运动速度基本一致;在伺服阀零漂因素影响下,系统内力仅受到系统内力空间基底变化和零漂的影响。
2) 在对冗余自由度进行力控制基础上,提出了基于Er−MCSI算法的内力抑制策略。对1个具有2个冗余自由度的六自由度液压驱动冗余并联机构仿的仿真结果表明:内力抑制后,作动器最大出力降低了21%,作动器最大内力降低了93%,系统的内力抑制效果得到明显改善。
[1] 罗中宝, 杨志东, 丛大成, 等. 2自由度驱动冗余摇摆台的设计[J]. 机器人, 2012, 34(5): 574−580.LUO Zhongbao, YANG Zhidong, CONG Dacheng, et al. Design of 2-DOF motion simulator with actuation redundancy[J]. Robot,2012, 34(5): 574−580.
[2] 何景峰, 李保平, 佟志忠, 等. 液压驱动冗余振动台自由度控制及内力协调[J]. 振动与冲击, 2011, 30(3): 74−78.HE Jingfeng, LI Baoping, TONG Zhizhong, et al. DOF control and inner force balancing of hydraulically redundant actuated shaking table[J]. Journal of Vibration and Shock, 2011, 30(3):74−78.
[3] CHEN J C, LIN T H, CHEN P C, et al. Advanced seismic testing using the multi-axial testing system (MATS) IN NCREE[C]//Proceedings of the 3rd International Conference on Advances in Experimental Structural Engineering. San Francisco, USA:Springer, 2009: 1−10.
[4] SADJADIAN H, TAGHIRAD H D. Kinematic, Singularity and stiffness analysis of the hydraulic shoulder: a 3-dof redundant parallel manipulator[J]. Advanced Robotics, 2006, 20(7):763−781.
[5] WEI Wei, YANG Zhidong, HAN Junwei, et al. Internal force decoupling control of hyper-redundant shaking table based on stiffness matrix[C]// Proceedings of the 2nd International Conference on Applied Mechanics and Materials. Kuala Laumpur, Malaysia: Trans Tech Publications, 2014: 115−120.
[6] MÜLLER A, HUFNAGEL T. Model-based control of redundantly actuated parallel manipulators in redundant coordinates[J]. Robotics and Autonomous Systems, 2012, 60(4):563−571.
[7] HE Jingfeng, JIANG Hongzhou, TONG Zhizhong. Modal control of a hydraulically driven redundant actuated fully parallel mechanism[J]. Journal of Vibration and Control, 2015, 23(10):1−8.
[8] PI Yangjun, WANG Xuanyin, GU Xi. Synchronous tracking control of 6-dof hydraulic parallel manipulator using cascade control method[J]. Journal of Central South University of Technology, 2011, 18(5): 1554−1562.
[9] PLUMMER A R. A general coordinate transformation framework for multi-axis motion control with applications in the testing industry[J]. Control Engineering Practice, 2010, 18(6):598−607.
[10] 关广丰, 熊伟, 王海涛, 等. 6自由度电液振动台控制策略研究[J]. 振动与冲击. 2010, 29(4): 200−203.GUAN Guangfeng, XIONG Wei, WANG Haitao, et al. Control strategy of a 6-DOF hydraulic shaker[J]. Journal of Vibration and Shock, 2010, 29(4): 200−203.
[11] UNDERWOOD M A, KELLER T. Applying coordinate transformations to multi-DOF shaker control[J]. Sound and Vibration, 2006, 40(1): 22−27.
[12] MERLET J P. Parallel robots[M]. Netherlands: Springer Science and Business Media, 2012: 281−286.
[13] di BERNARDO M, di GAETA A, MONTANARO U, et al.Experimental validation of the discrete-time MCS adaptive strategy[J]. Control Engineering Practice, 2013, 21(6): 847−859.
[14] CHELIHI A, CHEMACHEMA M. Model reference adaptive control for twin rotor multiple-input and multiple-output system via minimal controller synthesis[J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2014, 228(6): 406−418.
[15] MONTANARO U, OLM J M. Integral MRAC with minimal controller synthesis and bounded adaptive gains: the continuous-time case[J]. Journal of the Franklin Institute, 2016,353(18): 5040−5067.
[16] KOGANEZAWA K, STOTEN D P. Adaptive control of manipulators via an extension to the error-based minimal control synthesis with integral action algorithm[C]// IEEE International Conference on Robotics and Automation. Roma, Italy: IEEE,2007: 10−14.
Internal force analysis and rejection of hydraulically driven redundant parallel mechanism
GAO Changhong, YANG Zhidong, CONG Dacheng, HAN Junwei, YANG Chifu
(School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150001, China)
To analyze the internal force characteristics and reduce the internal force of hydraulically driven parallel mechanism, the internal force space and its basis were described firstly. The influence of different factors on internal force of the system was discussed under the freedom control framework. Then an internal force rejection strategy based on the error-based minimal control synthesis with integral action (Er−MCSI) algorithm was proposed for the HDRPM with high nonlinearity, time-varying parameters and external disturbance. Finally, taking a six degrees-of-freedom (DOF)HDRPM with two redundant DOF as an example, under the working conditions of equal displacement, equal velocity and equal acceleration, the influence of different factors on internal force of the system was investigated. The proposed internal force rejection strategy was implemented. The results show that the control method can online adjust the parameters adaptively online and reduce the internal force effectively.
hydraulically driven; redundant parallel mechanism; internal force rejection; minimal control synthesis
TP242.2
A
1672−7207(2017)11−2897−09
10.11817/j.issn.1672-7207.2017.11.008
2016−11−09;
2016−12−23
国家自然科学基金资助项目(51205077,51475116) (Projects(51205077, 51475116) supported by the National Natural Science Foundation of China)
丛大成,博士,教授,从事液压驱动冗余并联机构分析设计与控制研究;E-mail: congdacheng@fyty2010.com
(编辑 刘锦伟)

