表面扩散机制下金属纤维烧结过程的数值模拟

宋敏，郑洲顺，谌东东，曹稳，傅太白，汤慧萍

(1. 中南大学 数学与统计学院，湖南 长沙，410083；

2. 中南大学 机电工程学院，湖南 长沙，410083；

3. 西北有色金属研究院 金属多孔材料国家重点实验室，陕西 西安，710016)

表面扩散机制下金属纤维烧结过程的数值模拟

宋敏1，郑洲顺1，谌东东2，曹稳1，傅太白1，汤慧萍3

(1. 中南大学 数学与统计学院，湖南 长沙，410083；

2. 中南大学 机电工程学院，湖南 长沙，410083；

3. 西北有色金属研究院 金属多孔材料国家重点实验室，陕西 西安，710016)

基于金属纤维烧结结点的不同截面为椭圆−椭圆结构，建立金属纤维烧结过程的表面扩散模型。用有限差分法对该非线性微分方程组进行数值求解，实现金属纤维烧结结点形成过程的数值模拟。以夹角为0°，45°和90°的金属纤维为主要研究对象，对其烧结过程进行数值模拟。研究结果表明：在初始烧结阶段，烧结颈半径会迅速长大，随着烧结过程的进行烧结颈生长速度逐渐减小。在相同纤维夹角的条件下，在锐角平分线截面的烧结颈半径生长速度比在钝角平分线截面快；在不同纤维夹角的条件下，纤维夹角越大，在沿钝角平分线截面烧结颈半径生长速度越快，而在锐角平分线截面情况相反。

金属纤维；表面扩散；有限差分；烧结颈

金属纤维作为第三代金属多孔材料，不仅保留了金属固有的性能，又获得了某些特殊的物理性能，如导电性、导热性、导磁性和耐高温性等。金属纤维多孔材料凭借其独特的性能，在航空、电力、石油等众多领域得到广泛应用，已成为当前材料科学研究的前沿和热点[1−3]。目前，金属纤维烧结过程的研究多是以金属粉末烧结理论为基础的，金属粉末的烧结理论已经非常成熟。早在1965年，NICHOLS等[4]以表面扩散为物质迁移的主导机制，首次用计算机模拟了金属粉末烧结颈生长的变化趋势。随着计算机技术的迅速发展，金属粉末烧结颈生长过程的数学建模及数值模拟有了很大的进展，烧结模拟算法也越来越多，如有限元方法[5−7]、Level Set方法[8−10]等。然而，金属纤维烧结过程的研究还较少。20世纪60年代，PRANATIS等[11]研究了金属纤维的烧结机制，发现金属纤维多孔材料与金属粉末多孔材料的烧结机制存在明显差异。20世纪70年代，KOSTORNOV等[12]系统研究了材质与丝径不同的金属纤维的烧结过程，发现将金属纤维压制成形后进行烧结时，沿压力方向会出现先膨胀后收缩的现象。20世纪80年代，KOSTORNOV等[13]借助粉末烧结的黏性流动理论对金属纤维的烧结机制进行了初步研究。2003年，美国密歇根大学的 BERHAN等[14]基于有限元软件模拟了在熔化−凝固过程中纤维结点形成的三维结构。当然，我国的许多研究者也对金属纤维多孔材料的制备和应用进行了大量的研究。乔吉超等[15−16]对金属纤维多孔材料的力学性能及金属纤维电磁屏蔽材料进行了系统研究。WANG等[17]对FeCrAl纤维多孔材料的分形维数进行了相关研究，计算了孔结构的分形维数，并分析了放大倍数与孔隙度对分形维数的影响规律。CHEN等[18−20]基于水平集方法对表面扩散机制下金属纤维的烧结过程进行数值模拟，但是该数值方法运算量大，程序运行耗时长。金属纤维烧结结点对金属纤维材料的各项性能有着非常大的影响，所以对其形成过程展开研究具有重要意义。有限差分法已经是非常成熟的一种数值分析方法，在粉末注射成形[21]、电磁学[22]等诸多领域都有重要的应用，但是将有限差分法应用于金属纤维烧结过程的数值模拟目前仍少见报道。事实上，相对于水平集方法[18−20]、有限元方法[5−7]等其他数值解法，使用有限差分法对表面扩散模型进行数值求解更加简单易懂，便于实现。当然，有限差分法更大的优势体现在程序实现方面，在用Matlab进行编程计算时，相对于其他数值算法，其所占内存更小、算法实现耗时更少。所以，在工程实现方面，有限差分法一直被广泛应用。在数值模拟过程中，金属粉末被看作球体进行研究，球体具有完全对称的特点，所以对粉末烧结的研究可以简化到一维或是二维进行，如球球模型、球板模型[23]。而金属纤维被看作圆柱体进行研究，烧结过程不仅有径向的物质迁移，还存在沿金属纤维长度方向的轴向物质迁移。在三维情况下，对金属纤维烧结结点的研究是非常复杂的。为此，本文作者将相交金属纤维不同截面形成的椭圆−椭圆结构与表面扩散模型结合，建立新的数学模型，并用有限差分法进行数值模拟。对夹角为0°，45°和90°的金属纤维的角平分线所在截面进行二维数值模拟，探讨在不同截面上不同纤维夹角对金属纤维烧结颈的生长速度的影响。

1 金属纤维的表面扩散模型

烧结过程模拟的前提是建立烧结模型，模型建立的质量将直接影响到数值模拟的精度。考虑到烧结过程的复杂性，为了建立描述烧结过程的合理模型，将金属纤维假设为圆柱体；烧结过程中忽略重力的作用；烧结过程中金属纤维没有相对滑移和旋转。因为是烧结初期，故金属纤维的半径没有明显变化。

1.1 几何模型

假设2根金属纤维的夹角为α，以纤维夹角大的角平分线为极轴，如图1所示。在烧结结点处，沿极轴逆时针旋转β角方向取一截面，截面假设为椭圆−椭圆结构。图2所示为2根金属纤维烧结点处的截面，该坐标系为与极轴夹角为β方向的截面建立的笛卡尔坐标系，O1为左边金属纤维的截面，O2为右边金属纤维的截面，R为金属纤维的半径，Y为颈长。

根据图1和图2所示的几何关系，可以推导出2根金属纤维分别在各个方向截面上的函数表达式如下。

图1 2根夹角为α的金属纤维Fig. 1 Two metal fibers with angle ofα

图2 2根金属纤维烧结结点处的截面Fig. 2 Section of sintered node of two metal fibers

β(02πβ≤≤)的变化描述了烧结结点处各个方向的截面。在此，只研究0π/2β≤≤的情况，其他情况可以对称得出。

1.2 表面扩散模型

由 MULLINS[24]定义的表面扩散可以描述为：物质流动是由化学势梯度引起的，化学势梯度与表面流量成正比例关系，而表面流量与表面曲率的梯度成正比例关系，因此，表面扩散速度(物质流动速度)与表面流量梯度成正比例关系，可以表述为

式中：rn为表面法向量；t为时间；Js为表面流量；K为表面曲率；s为弧长；B为系数，

MULLINS[24]所定义的表面流量为

将式(5)代入式(3)可得

式(3)及式(5)中的变量量纲一化，得到：

根据金属纤维的几何模型建立表面扩散模型的初始边界条件，可以实现金属纤维烧结过程的数值模拟。

1.3 基于有限差分法的表面扩散模型

在直角坐标系下，表面扩散模型可以表示为

采用有限差分法求解上述模型，时间方向采用向前差分格式，时间步长为τ，网格剖分为N份，空间方向采用中心差分格式，空间步长为 h，网格剖分为M份，具体如下。

时间一阶差分格式为

空间一阶差分格式为

空间二阶差分格式为

所以，基于有限差分法的表面扩散模型为式中：

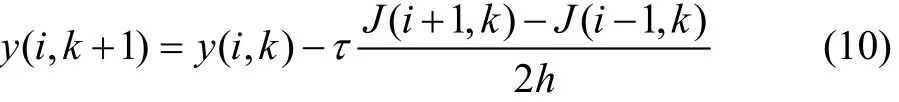
求解上述初始边值问题的偏微分方程，初始条件及边界条件的选取对于数值模拟结果的准确性有重要影响。假设烧结结点的坐标为(X, Y)，用“−”和“+”分别表示接触点左、右两边的截面，在研究表面扩散机制下金属纤维的烧结过程中有如下边界条件。

1) 整个表面在烧结结点处是连续的，即

2) 在烧结初始状态，在烧结结点处满足

3) 在x=±2R处，由MULLINS[24]的假设，系统边缘处 Js=0，这里同样作此假设。由于本文研究的是烧结初期，可以假设y(±2R,t)=0，Js(±2 R,t)=0。

2 数值模拟结果及讨论

基于 Matlab软件对金属纤维表面扩散模型进行数值求解，并将金属纤维的二维数值模拟结果与实际烧结实验的 SEM 图片进行对比，以证明本文模拟结果的可靠性。在数值模拟过程中，纤维初始半径(量纲为一)取为2，空间方向演化步数为200步，空间步长h取为0.04，时间方向演化步数取为100 000步，时间步长τ为金属纤维烧结结点处由初始状态至局部平衡(烧结结点处与相邻结点的弯曲程度相同)所需的时间，由Matlab计算得出。为了方便分析纤维夹角对烧结颈生长速度的影响，在此，所有情况取相同的时间段进行研究。

2.1 夹角为0°的金属纤维的数值模拟结果

对于夹角为0°的金属纤维，其数值模拟结果和实验结果分别如图3和图4所示，其颈半径生长曲线如图5所示。

由图3和图4可以看出：数值模拟结果与实验吻合较好。烧结初期纤维半径不会发生明显变化。由图5可知：在烧结的初始阶段，颈半径会迅速生长至约0.236，这是由于在烧结初期，烧结颈处的曲率梯度很大导致表面扩散的驱动力很大，烧结颈生长速度很快。随着烧结的进行，烧结颈的生长速度逐渐变慢并趋于平稳。

2.2 夹角为45°的金属纤维的数值模拟结果

对于夹角为 45°的 2根金属纤维，选取其钝角平分线截面和锐角平分线截面进行数值模拟。这2个截面的颈半径的生长趋势可以代表烧结过程中金属纤维颈半径的径向生长趋势和轴向生长趋势。2.2.1 钝角平分线方向的模拟结果

图3 平行金属纤维不同时刻截面的数值模拟结果Fig. 3 Numerical simulation results of section of parallel metal fiber at different time

图4 实际烧结过程平行金属纤维截面的实验结果Fig. 4 Experimental results of section of parallel metal fiber in actual sintering process

图5 平行金属纤维烧结颈半径生长曲线Fig. 5 Growth curve of sintering neck radius of parallel metal fiber

对夹角为 45°的金属纤维沿钝角平分线方向，其数值模拟结果和实验结果分别如图6和图7所示，颈半径的生长曲线如图8所示。

2.2.2 锐角平分线方向的模拟结果

对于夹角为 45°的金属纤维沿锐角平分线方向，其数值模拟结果和实验结果分别如图 9和图 10所示，颈半径的生长曲线如图11所示。

由图6、图9与图7、图10对比可以看出：数值模拟结果与实验结果较吻合。颈半径的生长趋势仍是先快后慢，然后逐渐趋于平稳。由图8和图11可知：钝角平分线颈半径生长速度明显低于锐角平分线颈半径的生长速度。

2.3 垂直金属纤维的数值模拟结果

对于垂直金属纤维，其钝(锐)角平分线方向数值模拟结果和实验结果分别如图12和图13所示，颈半径的生长曲线如图14所示。

图6 夹角为45°的金属纤维的钝角平分线截面的数值模拟结果Fig. 6 Numerical simulation results of section of bisector of obtuse angle of metal fiber with angle of 45°

图7 实际烧结过程钝角平分线截面的实验结果Fig. 7 Experimental result of section of bisector of obtuse angle in actual sintering process

图8 钝角平分线截面烧结颈半径生长曲线Fig. 8 Growth curve of sintering neck radius at section of bisector of obtuse angle

图9 夹角为45°的金属纤维锐角平分线截面的数值模拟结果Fig. 9 Numerical simulation results of section of bisector of acute angle of metal fiber with angle of 45°

图10 实际烧结过程锐角平分线截面的实验结果Fig. 10 Experimental result of section of bisector of acute angle in actual sintering process

图11 锐角平分线截面烧结颈半径生长曲线Fig. 11 Growth curve of sintering neck radius at section of the bisector of acute angle

由图12与图13可以看出：当纤维夹角为90°时，数值模拟结果与实验结果比较吻合。由图14可知：颈半径的生长趋势仍然是先快后慢，并逐渐趋于平稳。

2.4 纤维夹角对烧结颈生长速度的影响

表面扩散是由表面曲率梯度驱动的。纤维与纤维刚刚接触时，烧结结点处存在巨大的曲率差，导致烧结开始时，烧结颈迅速生长以达到烧结结点处的局部平衡，即烧结结点处与相邻点的弯曲程度相同。对于不同截面，烧结颈迅速生长的速度是不同的。所以为了分析纤维夹角对颈半径生长速度的影响，在原有纤维夹角0°，45°和90°的数值模拟基础上又添加了30°及 60°夹角的金属纤维的数值模拟。不同夹角的金属纤维在钝角平分线及锐角平分线截面的颈半径生长速度曲线如图15和图16所示。

图12 垂直金属纤维不同时刻截面的数值模拟结果Fig. 12 Numerical simulation results of section of vertical metal fibers at different time

图13 实际烧结过程中钝(锐)角平分线截面的实验结果Fig. 13 Experimental result of section of bisector of obtuse(acute) angle in actual sintering process

图14 垂直金属纤维烧结颈半径生长曲线Fig. 14 Growth curve of sintering neck radius of vertical metal fiber

图 15 纤维夹角为 0°, 30°, 45°, 60°, 90°时，钝角平分线方向烧结颈半径生长曲线Fig. 15 Growth curves of sintering neck radius along bisector of obtuse angle with fiber angle of 0°, 30°, 45°, 60°, 90°

图 16 纤维夹角为 30°, 45°, 60°, 90°时，锐角平分线方向烧结颈半径生长曲线Fig. 16 Growth curves of sintering neck radius along bisector of acute angle with fiber angle of 30°, 45°, 60°, 90°

由图15和图16可知：在钝角平分线截面上，纤维夹角越大，颈半径生长速度越快，而在锐角平分线截面上，情况则相反；锐角平分线截面上颈半径生长速度比钝角平分线截面快很多；纤维之间距离越近，烧结颈越容易形成，生长速度越快，形成的烧结颈越大。因此，金属纤维夹角对烧结颈的形成起重要作用。

3 结论

1) 将金属纤维的几何结构与传统的表面扩散模型结合，建立相交金属纤维的表面扩散模型。此模型是一个非线性微分方程组，用有限差分法对其进行数值求解，实现了金属纤维烧结过程的数值模拟。

2) 所用的有限差分法简单易懂、便于实现，相对于水平集方法等其他数值算法，所占内存小、耗时少，在工程实现方面更有优势。

3) 研究了不同夹角的金属纤维在钝角平分线截面及锐角平分线截面上颈半径的生长趋势，锐角平分线截面的烧结颈生长速度比钝角平分线截面的烧结颈生长速度快。

4) 夹角越大，锐角平分线截面烧结颈生长速度越慢，烧结颈越小；而在钝角平分线截面情况相反。

[1] ZHOU Zhi, SHEN Xiangqian, SONG Fuzhan, et al. Structures and magnetic properties of nanocomposite CoFe2O4-BaTiO3fibers by organic gel-thermal decomposition process[J]. Journal of Central South University, 2010, 17(6): 1172−1176.

[2] 苏堤, 黄伯云. 金属纤维增强型摩擦材料与灰铸铁滑动摩擦性能[J]. 中南大学学报(自然科学版), 2007, 38(4): 583−588.SU Di, HUANG Baiyun. Properties of metal fibers reinforced friction materials and gray cast iron friction couple[J]. Journal of Central South University (Science and Technology), 2007, 38(4):583−588.

[3] HAO Kuansheng, HUANG Songling, ZHAO Wei, et al.Modeling and finite element analysis of transduction process of electromagnetic acoustic transducers for nonferromagnetic metal material testing[J]. Journal of Central South University, 2011,18(3): 749−754.

[4] NICHOLES F A, MULLINS W W. Morphological changes of a surface of revolution due to capillarity-induced surface diffusion[J]. Journal of Applied Physics, 1965, 36(6):1826−1832.

[5] CH’NG H N, PAN Jingzhe. Sintering of particles of different sizes[J]. Acta Materialia, 2007, 55(3): 813–824.

[6] MUNOZ P D, BRUCHON J, DRAPIER S, et al. A finite element-based level-set method for fluid-elastic solid interaction with surface tension[J]. International Journal for Numerical Methods in Engineering, 2013, 93(9): 919−941.

[7] YUE Pengtao, ZHOU Chunfeng, FENG James J, et al.Phase-field simulations of interfacial dynamics in viscoelastic fluids using finite elements with adaptive meshing[J]. Journal of Computational Physics, 2006, 219(1): 47−67.

[8] BRUCHON J, DRAPIER S, VALDIVIESO F. 3D finite element simulation of the matter flow by surface diffusion using a level set method[J]. International Journal for Numerical Methods in Engineering, 2011, 86(7): 845−861.

[9] 谌东东, 郑洲顺, 汤慧萍, 等. 基于表面扩散机制金属纤维烧结的三维模拟[J]. 稀有金属材料与工程, 2016, 45(11):2912−2917.CHEN Dongdong, ZHENG Zhoushun, TANG Huiping, et al.The three-dimensional simulation of metal fibers by surface diffusion[J]. Rare Metal Materials and Engineering, 2016, 45(11):2912−2917.

[10] PINO-MUNOZ D, BRUCHON J, DRAPIER S, et al. Sintering as particle scale: an Eulerian computing framework to deal with strong topological and material discontinuities[J]. Archives of Computational Methods in Engineering, 2014, 21(2): 141−187.

[11] PRANATIS A L, SEIGLE L. Powder metallurgy[C]//Proceedings of International Conference on Powder Metallurgy.New York, USA: Interscience, 1961: 53−73.

[12] KOSTORNOV A G, KIRICHENKO O V, BRODIKOVSKII N P,et al. High-porous materials of carbon steel fibers and their mechanical properties[J]. Poroshkovaya Metallurgiya, 2008,47(3/4): 21−26.

[13] KOSTORNOV A G, KIRICHENKO O V, BRODIKOVSKII N P,et al. High-porous Materials made from alloy steel fibers:production, structure, and mechanical properties[J]. Poroshkovaya Metallurgiya, 2008, 47(5/6): 39−44.

[14] BERHAN L, SASTRY A M. On modeling bonds in fused,porous networks: 3D simulations of fibrous-particulate joints[J].Journal of Composite Materials, 2003, 37(8): 715−740.

[15] 乔吉超, 奚正平, 汤慧萍, 等. 金属纤维多孔材料力学性能的研究进展[J]. 稀有金属材料与工程, 2009, 38(3): 267−270.QIAO Jichao, XI Zhengping, TANG Huiping, et al. The study of mechanical properties of metal fiber porous material[J]. Rare Metal Materials and Engineering, 2009, 38(3): 267−270.

[16] 王建忠, 奚正平, 汤慧萍, 等. 金属纤维电磁屏蔽材料的研究进展[J]. 稀有金属材料与工程, 2011, 40(9): 1687−1691.WANG Jianzhong, XI Zhengping, TANG Huiping, et al. Metal fiber electromagnetic shielding material investigation[J]. Rare Metal Materials and Engineering, 2011, 40(9): 1687−1691.

[17] WANG Jianzhong, XI Zhengping, TANG Huiping, et al. Fractal dimension for porous metal materials of FeCrAl fiber[J].Transactions of Nonferrous Metals Society of China, 2013, 23(4):1046−1051.

[18] CHEN Dongdong, ZHENG Zhoushun, WANG Jianzhong, et al.Three-dimensional simulation of sintering crunodes of metal powders or fibers by level set method[J]. Journal of Central South University, 2015, 22(7): 2446−2455.

[19] CHEN Dongdong, ZHENG Zhoushun, WANG Jianzhon, et al.2D model and 3D reconstitution of sintering metal fibers by surface diffusion[J]. Rare Metal Materials and Engineering, 2017,46(6): 1474−1479.

[20] CHEN Dongdong, ZHENG Zhoushun, WANG Jianzhong, et al.Modeling sintering behavior of metal fibers with different fiber angles[J]. Rare Metals, 2016, 35: 1−8.

[21] 封娟, 何浩, 李益民, 等. 粉末共注射成形充模流动过程前沿位置及场分布的数值模拟[J]. 中国有色金属学报, 2012, 22(8):2333−2339.FENG Juan, HE Hao, LI Yimin, et al. Numerical simulation of melt front and field profile in powder co-injection molding filling process[J]. The Chinese Journal of Nonferrous Metals,2012, 22(8): 2333−2339.

[22] 黄丽, 蒋练军, 张学军, 等. 基于高阻抗表面材料电磁特性的矩形波导[J]. 中南大学学报(自然科学版), 2012, 43(10):3913−3916.HUANG Li, JIANG Lianjun, ZHANG Xuejun, et al.Rectangular wave guide based on electromagnetic characteristics of high impedance surface material[J]. Journal of Central South University (Science and Technology), 2012, 43(10): 3913−3916.

[23] 朱院院. 烧结初期阶段颈长动态模拟[D]. 西安: 西安理工大学材料加工工程学院, 2006: 8−10.ZHU Yuanyuan. The dynamic simulation of early stages of sintering neck[D]. Xi’an: Xi’an University of Technology.School of Material Processing Engineering, 2006: 8−10.

[24] MARTIN P. Thermal grooving by surface diffusion: Mullins revisited and extended to multiple grooves[J]. Quarterly of Applied Mathematics, 2009, 67(1): 125−136.

Numerical simulation of metal fiber sintering by surface diffusion

SONG Min1, ZHENG Zhoushun1, CHEN Dongdong2, CAO Wen1, FU Taibai1, TANG Huiping3

(1. School of Mathematics and Statistics, Central South University, Changsha 410083, China;2. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;3. State Key Laboratory of Porous Metal Materials, Northwest Institute for Nonferrous Metal Research,Xi’an 710016, China)

Based on the oval-oval structure of different sections of two intersecting metal fiber sintered node, the surface diffusion model of the sintering process of metal fibers was established. This model, which was the nonlinear partial differential equations, could be numerically solved by finite difference method, and the numerical simulation of the forming process of metal fiber sintered node could be realized. Focus on the metal fibers with the angle of 0°, 45°, and 90°, the numerical simulations were conducted, respectively. The results show that the sintering neck radius quickly grows in the initial sintering stage, and then the growth rate decreases gradually in the following sintering process. Under the condition of the same fiber angle, the neck radius at the section of the bisector of acute angle grows much faster than that at the section of the bisector of obtuse angle. Under the condition of different fiber angles, the larger the fiber angle is,the faster the growth rate of sintering neck at the section of the bisector of obtuse angle grows, and the situation at the section of the bisector of acute angle is opposite.

metal fiber; surface diffusion; finite difference; sintering neck

TG111.6

A

1672−7207(2017)11−2851−08

10.11817/j.issn.1672-7207.2017.11.002

2016−11−03；

2016−12−24

国家自然科学基金资助项目(51174236)；国家重点基础研究发展计划(973计划)项目(2011CB606306)；金属多孔材料国家重点实验室开放基金资助项目(PMM-SKL-4-2012)；中南大学研究生创新项目(2016zzts220) (Project(51174236) supported by the National Natural Science Foundation of China; Project(2011CB606306) supported by the National Basic Research Development Program (973 Program) of China; Project(PMM-SKL-4-2012) supported by the National Key Laboratory Open Program of Porous Metal Material of China;Projects(2016zzts220) supported by the Innovation Project of Central South University)

郑洲顺，博士，教授，从事偏微分方程数值解及数值模拟研究；E-mail: 2009zhengzhoushun@163.com

(编辑 刘锦伟)