电能质量分析中的谐波分析方法注释

陈明卿

国网福州供电公司

电能质量分析中的谐波分析方法注释

陈明卿

国网福州供电公司

谐波的测量及分析是电能质量分析中的一个重点环节，本文分析了谐波分析及谐波的危害，并明确了电能质量分析下的谐波指标，给出了电能质量分析中的谐波测量方式及公式推导，为研究人员提供借鉴。

电能质量；谐波；分析方法

前言：

伴随着电子技术的发展，电子设备对电力系统产生的干扰尤其是谐波干扰，次数越来越多，危害越来越大。谐波对电力系统、电力设备及通讯等都会造成极大的影响。伴随着生活中电气设备越来越多，谐波对于群众生活的影响也越来越大，谐波问题日益严峻，谐波的测量及分析为谐波问题的解决提供依据，其重要程度有所深化，测量是分析谐波并解决谐波问题的重点内容。

一、谐波分析及谐波的危害分析

(一)谐波分析

简谐运动的处理相对简单，但大多数振动系统的运动不是简谐运动。大多数情况下的振动为周期运动，关于时间的周期函数都能够展开为傅里叶级数，成为无限多的正弦函数以及余弦函数和表示，学术上将此分析模式称作谐波分析。

(二)谐波的危害

在现实生活中，谐波会使公用电网中的电力元件产生谐波损耗，从而降低发电、输电及用电效率，导致电能的浪费，有研究表明，大量的三次谐波流经中性线会导致整体线路过热，埋下火灾隐患，对用电稳定及安全造成影响。谐波会导致电容、电缆设备过热过载、绝缘老化，降低使用寿命。最后谐波还会引起继电保护等自动装置的误动作，电气仪表精准度降低，同时会对周围的通讯系统等其他信号进行干扰，降低通讯接收质量[1]。

二、电能质量分析下的谐波指标

严格的说，谐波指的是电流中蕴含的频率以及基波整数倍的电量，一般情况下是指对周围非正弦电量进行傅里叶变换级数分解，其他的大于基波频率电流所产生的电量。

谐波会增加输电、输电及用电设备的损耗，导致设备的温度过高，影响设备使用的经济效益。谐波电流使输电线路上是电能损耗增加，谐波频率会在网络谐振点周围对电力电缆线路及输电线路造成绝缘击穿。谐波电压增加变压器损耗，影响绝缘强度，也增加了铜损。

谐波影响了几点保护及自动装置工作的可靠。电磁继电器会因为谐波导致继电器错误动作或是不发出动作，对电力运行安全带来极大威胁。在电力线路上经过的幅值较大的奇数次低频谐波电流通过磁场耦合，会对周围通讯产生干扰电压，影响通话质量。也会使图形设备如电视、计算机显示器的显示畸变，影响使用[2]。

三、电能质量分析中的谐波测量方式及公式推导

(一)电能质量分析中的谐波测量方式

现阶段所应用到的谐波测量方式有四种。

第一种傅里叶变换。对电力系统运行中的电压及电流同步进行采样，之后应用离散傅里叶变换或是快速傅里叶变换，处理所采集的信息，对信息进行频谱分析，从而计算出谐波的幅值以及初相位角。傅里叶变换法的缺点在于，在信号采样采集时难以保证采样的同步性，其原因在于对信号频率进行精准预测的难度较大，只能是根据上一周期所采集的信号频率对下一周期的采样信号频率进行估算，再显示出换算的频率。对于采样的信号的频率难以同步，且谐波计算的分辨率难以达到最高水平，导致傅里叶变换的频段波普出现泄露情况以及栅栏效应，最终影响谐波测量数据以及测量结果的精准性。我们可以应用加窗函数的方法拟性计算以降低频谱泄露及栅栏效应所产生的误差。

举例说明傅里叶变换法的应用：

假设我们有一个信号，它含有2V的直流分量，频率为50Hz、相位为-30度、幅度为3V的交流信号，以及一个频率为75Hz、相位为90度、幅度为1.5V的交流信号。用数学表达式就是如下：S=2+3*cos(2*pi*50*t-pi*30/180)+1.5*cos(2*pi*75*t+pi*90/180)。式中cos参数为弧度，所以-30度和90度要分别换算成弧度。我们以256Hz的采样率对这个信号进行采样，总共采样256点。按照我们上面的分析，Fn=(n-1)*Fs/N，我们可以知道，每两个点之间的间距就是1Hz，第n个点的频率就是n-1。我们的信号有3个频率：0Hz、50Hz、75Hz，应该分别在第1个点、第51个点、第76个点上出现峰值，其它各点应该接近0。

按照公式，可以计算出直流分量为：512/N=512/256=2；50Hz信号的幅度为：384/(N/2)=384/(256/2)=3；75Hz信号的幅度为192/(N/2)=192/(256/2)=1.5。可见，从频谱分析出来的幅度是正确的。

第二种方法是小波变换，即应用小波变换对谐波进行测量、计算和分析，此方法具备优秀的时域及频域局部性，但是因为小波变换所蕴含的固有特征即能量过于分散，频段分布不严谨且在谐波分析中容易出现频谱混叠的情况，最终导致频域分析存在误差。

第三种方法为瞬间无功功率理论，及应用瞬间无功功率理论对谐波进行计算，此方法在应用中具备优秀的时效性，但如果想分别对各次谐波的幅值及初相位角度进行计算，还是有很大难度的，并且在应用中需要较高的成本，对系统造成巨大的损耗。

第四种的计算方法为神经网络理论，应用神经网络理论对谐波进行计算，应用此方法可以使谐波计算具备自适应及自主学习能力，但现阶段，此方法还处在起步期，对此方法的研究及应用都不够成熟，投入使用还需要未来一段时间内仔细考究。

举例说明神经网络理论：

图1 模拟谐波测量装置

用ANN来替代图1所示的那组带通滤波器和检波器。让ANN的输入是待测量信号，相当于图1中放大器的输出信号。离线训练时它是信号在一个周期的采样值，而在线训练时它是信号的一系列时延值。ANN的输出对应于图1所示的检波器输出信号。它们得出的是所要测量的各次谐波信号(频率分别为f1， f2， …， fn)的幅值；输出为零就意味着待测量中不含某次谐波。按上述原理组成的ANN谐波测量电路示于图2。如果ANN的结构适当，算法选择可行，并用合理的样本进行充分训练，一旦给训练好的ANN加上所要测量的信号，那么在各个输出端就会实时得出待测量波形中含有的各次谐波幅值。

(二)电能质量分析中的谐波公式推导

因为傅里叶的变换计算具有很高的精度及便利性，且可应用功能多样，使傅里叶变换法成为现阶段嗲能质量谐波分析中最广泛应用的方法。介绍傅里叶变换计算谐波幅值以及初相位角的公式进行推到的计算公式。

其中A0为直流分量，ak为k次电压谐波分量的幅值，Φk为第k次的电压谐波分量的初相位角，基波的周期为T0，采样的周期为Ts，ω0是基波角速度即2π/T0，基频f0为50赫兹。应用的频率为fs，第n次采样时间t为nTs，假设连续时间为间隔采样所得的离散电压信号，其数值为us[N]，N为采样点数，在此情况下Ts/T0=1/N，f0/fs=1/N。则形式2变换为：

我们将3式的K次谐波进行离散傅里叶变换计算，得出结果：

将4式简化即可得出：

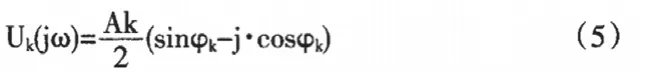
应用连续的时间等间隔对离散电压的信号值进行采样，最后进行离散傅里叶变换，可以得出：

如果4式和5式相等，那么

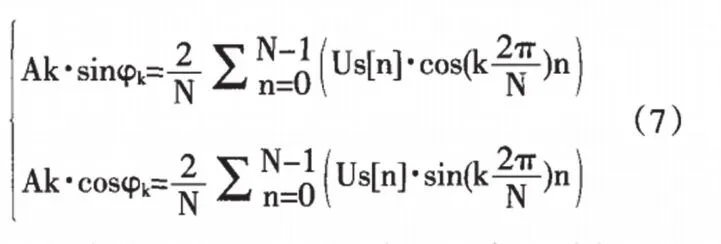
为了能够降低因为采样频率不同以及信号频率的差异、频率分辨率的不足对频谱泄露及栅栏效应的影响，可以在时域上添加窗函数。窗函数所应用的类型要参照测量进行选定，其中一种类型具有快速衰减的旁瓣值窗函数；另一种则是给定旁瓣幅值厚，主瓣宽度值最低的窗函数。

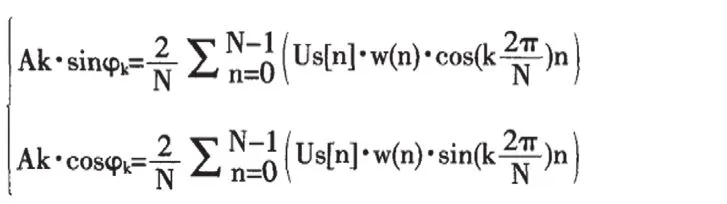
应用次推导公式所得到的第k次谐波的幅值与初相位角的计算公式则为：

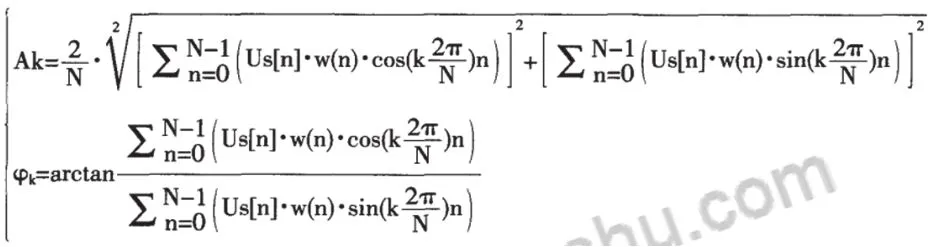
电流谐波的幅值与初相位角的计算推导公式与电压谐波幅值及初相位角的计算公式相同[3]。

总结：

文章列举了常用的四种谐波处理方式，分析了消除频谱泄露及栅栏效应的窗函数选择，并对谐波幅值、初相位角的计算公式进行了详细推导。谐波幅值、初相位角的计算推到具备一般性，为了能够使傅里叶变换计算电力系统谐波幅值及初相位角提供了可用公式。计算谐波幅值及初相位角的公式可通过上述公式进行应变，最终能够在各种情况下对谐波进行测量。

[1]孙松源.电能质量分析中的谐波分析方法注释[J].安徽电子信息职业技术学院学报，2016，15(3)：31-33.

[2]程凯.基于小波变换和傅立叶变换的电能质量分析方法[J].电子技术与软件工程，2016(14)：230-230.