一类积微分方程的加权伪概自守解*

卢丑丽

(山西农业大学信息学院,山西 晋中 030800)

一类积微分方程的加权伪概自守解*

卢丑丽

(山西农业大学信息学院,山西 晋中 030800)

加权伪概自守函数是较伪概自守函数和渐近概自守函数更一般的一类函数，在Banach空间中，利用Banach稳定点定理和算子理论的相关知识，得到一定条件下一类积微分方程的加权伪概自守解的存在性定理.

加权伪概自守函数，演化族，指数稳定性

引言

S.Bocher教授首次提出概自守函数理论后，该理论被国内外学者广泛研究[2～7].在文[2]、[3]中，作者给出了概自守函数的一些重要理论.该理论应用于Banach空间微分方程的伪概自守解的存在性和唯一性成了研究热点[2～6],其中肖体俊，梁进等证明(PAA(X),‖·‖∞) 空间是Banach空间，得到微分方程伪概自守解的存在性和唯一性的充分条件.J.Blot等学者在文[7]中介绍了加权伪概自守函数的理论，给出了加权伪概自守函数的完备定理和复合定理，以及在微分方程中的一些应用.在Banach空间X中，本文研究以下方程

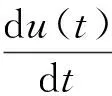
(1)

在初值条件：

u(0)=u0+g(u)

(2)

下的加权伪概自守解的存在性和唯一性，其中A,B(t)为X中稠定线性算子，u0∈X.

1 预备知识

本文中假设R为实数集，R+为X中非负子集.B(X)为X中有界线性算子，Cb(R,X)为R到X的全体有界连续函数，令K⊂X,T⊂R，定义Ck(T×X,X)为K上一致连续函数，即∀ε>0,∃δ>0,

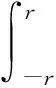
定义1[5]X上连续线性算子族{R(t):t≥0}称为一个演化族.如果满足以下条件：

(A1)R(0)=I，即为恒等算子；

(A2)对∀x∈X，[0,+∞)→X上的映射t→R(t)x连续；

(A3)对∀t≥0，R(t)为Y上连续算子，且对∀y∈Y，映射t→R(t)y在集合C([0,+∞),Y)∩C1([0,+∞),X)中，满足：

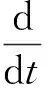
其中∀t≥0，Y=D(A)=D(B(t))，其范数为图像范数.

如果方程(1)的演化族R(·)存在，则定义其温和解如下：

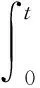
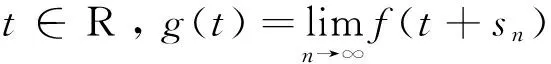
注1： 概自守函数Rf={f(t):t∈R}在X中是相对紧集，因此依范数有界.

定义4 如果有界函数f:R×Ω→X对任意t∈R,x∈K，f(t,x)为概自守函数，其中K为X中有界子集，则称为概自守函数，记为AA(R×Ω,X).

对∀ρ∈U∞，定义

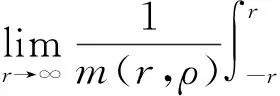
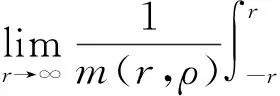
定义5 有界函数f:R→X(f:R×X→X)称为加权伪概自守函数，如果满足f=g+φ，其中g∈AA(X)(g∈AA(R×X,X)，φ∈PAA0(R(R×X),X).记WPAA(R,X)(WPAA(R×X,X))为加权伪概自守函数集.

注2： 若ρ=1，则WPAA(R,X)(WPAA(R×X,X))为伪概自守函数集.

引理2 若ρ∈Ub，令‖f‖WPAA(R,ρ)=supt∈R|f(t)|，则(WPAA(R,ρ),‖·‖WPAA(R,ρ))是Banach空间.

2 主要结论

为了方便得出结论，先做以下假设：

(B1)方程(1)存在指数稳定的演化族R(·)，即∃M,ω>0,s.t.‖R(t)‖≤Me-ω t.

(B2)f=g+φ∈WPAA(R×X,ρ)，且对任意t∈R,函数f(t,x),g(t,x)在有界子集K⊂X上一致连续.

(B3) 存在函数Lf:R+→R+使得对任意的t∈R+,r≥0,‖u‖,‖v‖≤r，有：

‖f(t,u)-f(t,v)‖≤Lf(r)‖u-v‖.

(B4)函数g:C(R+,X)→X满足李普希兹条件，即存在函数Lg:R+→R+使得对任意的r≥0,‖u‖,‖v‖≤r，有‖g(u)-g(v)‖≤Lg(r)‖u-v‖.

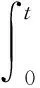
证明：注意到f是加权伪概自守函数且满足条件(B2)，由文献[7]中引理2.10可得f(t,x(t))∈WPAA(R,ρ).令f(t,x(t))=h(t)+φ(t)，其中h∈AA(X),φ∈PAA0(R,ρ)，则:

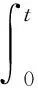
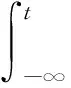
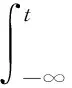
根据文献[5]中引理3.1和标注3.3可知,G(t)为概自守函数.

为了证明F(t)∈WPAA(R,ρ)，需验证H(t)∈PAA0(R,ρ)，也即证明:

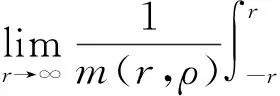
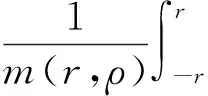
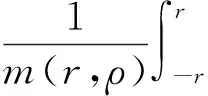
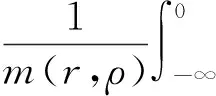
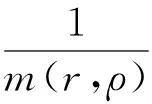
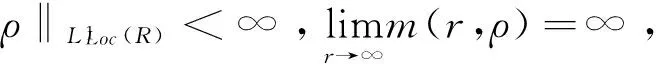
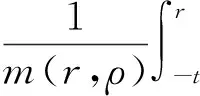
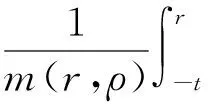
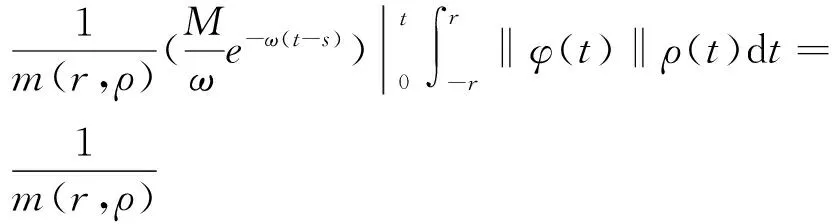
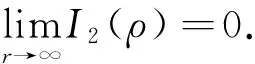
定理1 假设(B1)～(B5)均成立，则方程(1)、(2)存在唯一的加权伪概自守解.

证明：由条件(B5)可得，存在常数r>0满足

(3)

令E={u∈WPAA(R+,ρ);‖u‖≤r}，则E为WPAA(R+,ρ)的一个闭子集.定义E上一个算子V，即

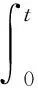
下面来验证V为WPAA(R+,ρ)上的一个映射.

易知V连续，再由引理3，有

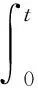
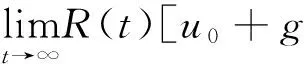
接下来，对于任意给定的u∈E，证明Vu∈E，也就是充分的说明‖Vu‖≤r，

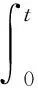
即对任意t≥0,有‖Vu‖≤r.

对任意的u,v∈E,t≥0，有:

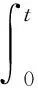
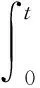
所以V是E上的压缩映射，由引理2，WPAA(R+,ρ)完备.因此根据Banach稳定点定理，方程(1)、(2)存在唯一的加权伪概自守解.证毕.

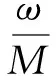
证明：注意到

ω(‖u0‖+‖g(0)‖+sups∈R‖f(s,0)‖<+∞

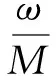
又根据定理1的证明，可得方程(1)、(2)存在唯一的加权伪概自守解u(t)∈WPAA(R+,ρ).

3 应用

例考虑下面方程的加权伪概自守解的存在性：

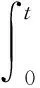
(4)

其初值条件为u(t,0)=u(t,π)=0

D(A)={u∈X:u''∈X,u(0)=u(π)=0}，

则方程(4)可以重新改写成方程(1)，从而方程(4)存在唯一的加权伪概自守解.

[1] Bochner.S. A new approach to almost-periodicity [J]. Proc.Natl.Acad.Sci.USA, 1962, 48: 2039-2043.

[2] XIAO Ti-jun, Jin Liang, Zhang Jun. Pseudo almost automorphic solutions to semilinear differential equations in Banach spaces [J].Semigroup Forum, 2008, 76: 518-524.

[3] XIAO Ti-jun, ZHU X.X., LIANG Jin.. Pseudo-almost automorphic mild solutions to nonautonomous differential equations and applications [J]. Nonlinear Anal, 2009, 70: 4079-4085.

[4] DING Hui-Sheng., XIAO Ti-Jun., LIANG Jin. Asymptotically almost automorphic solutions for some integrodifferential equations with nonlocal initial conditions [J].Journal of Mathematical analysis and applications,2008,338: 141-151.

[5] LIU Jing-huai, SONG Xiao-qiu. Almost automorphic and weighted pseudo almost automorphic solutions of semilinear evolution equations[J]. Journal of Function analysis, 2010, 11: 196-207.

[6] LIU Jing-huai, SONG Xiao-qiu, LU Feng-ling. Almost automorphic and pseudo almost automorphic solutions of semilinear evolution equations[J]. Acta Analysis Functionalis Applicata , 2009, 258: 294-300.

[7]Blot, J Mophou G.M., Guerekata G.M.N, et al. Weighted pseudo almost automorphic functions and applications to abstract differential equations [J]. Nonlinear Anal. ,2009, 71: 903-909.

[8]A.Pazy. Semigroups of linears Operators and Appliations to partial differential equations [M].Springer-Verlag, Newyork, Berlin, Heidelberg, Tokyo,1983.

[9]T.Diagana. Weighted pseudo almost periodic functions and applications [J]. C.R.Acad.Paris.ser.I,2006, 343(10): 643-646.

[10]T.Diagana. Weighted pseudo almost periodic solutions to some differential equations [J]. Nonlinear Anal.,2008, 68: 2250-2260.

[11]T.Diagana. Existence of weighted pseudo almost periodic solutions to some classes of hyperbolic evolu-tion equations [J]. J.Math Anal.Appl., 2009, 350: 18-28.

[12]T.Diagana. Weighted pseudo almost periodic solutions to a neutral delay integral equation of advanced type [J]. Nonlinear Anal.. 2009, 70: 298-304.

[13]ZHANG L., XU Y.. Weighted pseudo-almost periodic solutions of a class of abstract differential equa- tions [J]. Nonlinear Anal.,2009, 71: 3705-3714.

[14]LU chouli, SONG xiao-qiu,ZHANG rongjuan, Almost automorphic and weighted pseudo almost automorphic solutions to some semilinear differential equations[J].南京大学学报(数学半年刊),2012,29(2):105-114.

AClassofWeightedPseudoAlmostAutomorphicSolutiontoIntegroDifferentialEquations

LU Chou-li

(College of Information, Shanxi Agricultural University，Jinzhong Shanxi 030800，China)

Weighted pseudo almost automorphic function is more general than pseudo almost automorphic function and asymptotically almost automorphic function. Using Banach stable point theorem and operator theory knowledge, it gets a class of existence theorem of integro differential equations in Banach space.

weighted almost automorphic function; evolution family; exponential stability

1673-2103(2017)05-0011-05

2017-06-29

卢丑丽(1985-)，女，山西忻州人，讲师，硕士，研究方向：应用泛函分析及算子理论.

O177.5

A