2012—2017年高考立体几何题的统计分析

朱远彰

【摘 要】本文摘引分析 2012—2017 年高考立体几何试题，归纳出命题的重点及规律，提出相应的复习策略，并选择部分试题进行分析和讲解，以便读者参考。

【关键词】高考立体几何 试题分析 应考策略

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2017）09B-0152-05

立体几何，高中数学内容的一个大模块，也是重要的模块之一，每年高考必考。它主要考查学生的空间想象能力、逻辑推理能力、综合应用能力、运算能力等。纵观近几年的高考数学题，立体几何都是两个小题（有一个三视图）加一个大题；大题基本固定在 18 或 19 题的位置，属于中档题，是考生拉大分数差距的必做题之一，是高分考生竞相角逐的地方。

高考中的立体几何题量与难度的编排如此有规律，使我们不得不引起重视，且分值较高，值得我们好好分析与研究。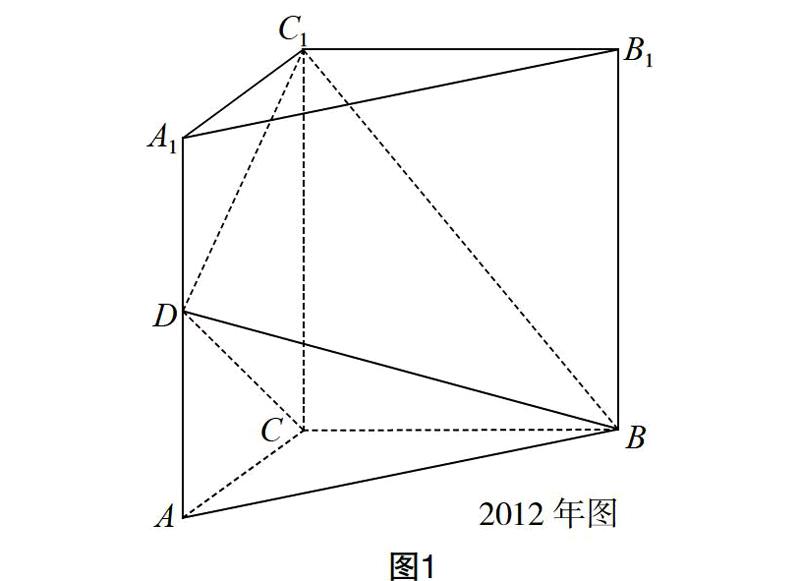

一、2012—2017年高考中的立体几何解答题摘引

1.2012理（19）（本小题满分12分）

如图 1，直三棱柱 ABC-A1B1C1 中，AC=BC=AA1，D 是棱 AA1 的中点，DC1⊥BD。

（1）证明：DC1⊥BC；

（2）求二面角 A1-BD-C1 的大小。

2.2012文（19）（本小题满分12分）

如图 1，三棱柱 ABC-A1B1C1 中，侧棱垂直底面，∠ACB=90°，AC=BC=AA1，D 是棱 AA1 的中点。

（I）证明：平面 BDC1⊥平面 BDC；

（Ⅱ）平面 BDC1 分此棱柱为两部分，求这两部分体积的比。

3.2013理（18）（本小题满分12分）

如图 2，三棱柱 ABC-A1B1C1 中，CA=CB，AB=AA1，∠BAA1=60°。

（Ⅰ）证明 AB⊥A1C；

（Ⅱ）若平面 ABC⊥平面 AA1B1B，AB=CB=2，求直线 A1C 与平面 BB1C1C 所成角的正弦值。

4.2013文（19）（本小题满分12分）

如图 2，三棱柱 ABC-A1B1C1 中，CA=CB，AB=AA1，∠BAA1=60°。

（Ⅰ）证明：AB⊥A1C；

（Ⅱ）若 AB=CB=2，A1C=，求三棱柱 ABC-A1B1C1 的体积。

5.2014理（18）（本小题满分12分）

如图 ?3，四棱锥 P?-ABCD 中，底面 ABCD 为矩形，PA⊥平面 ABCD，E 为 PD 的中点。

（1）证明：PB∥平面 AEC；

（2）设二面角 D?-AE?-C 为 60°，AP=1，AD=，

求三棱锥 E?-ACD 的体积。

6.2014文（18）（本小题满分12分）

如图 3，四棱锥 P?-ABCD 中，底面 ABCD 为矩形，PA⊥平面 ABCD，E 为 PD 的中点。

（Ⅰ）证明：PB∥平面 AEC；

（Ⅱ）设 AP=1，AD=，三棱锥 P﹣ABD 的體积 ，求 A 到平面 PBC 的距离。

7.2015理（19）（本小题满分12分）

如图 4，长方体 ABCD-A1B1C1D1 中，AB=16，BC=10，AA1=8，点 E，F 分别在 A1B1，D1C1 上，A1E=D1F=4，过点 E，F 的平面 与此长方体的面相交，交线围成一个正方形。

（1）在图中画出这个正方形（不必说明画法和理由）；

（2）求直线 AF 与平面 所成的角的正弦值。

8.2015文（19）（本小题满分12分）

如图 4，长方体 ABCD-A1B1C1D1 中 AB=16，BC=10，AA1=8，点 E，F 分别在 A1B1，D1C1 上，A1E=D1F=4，过点 E，F 的平面 与此长方体的面相交，交线围成一个正方形。

（I）在图中画出这个正方形（不必说明画法与理由）；

（II）求平面 把该长方体分成的两部分体积的比值。

9.2016理（19）（本小题满分12分）

如图 5，四棱锥 P-ABCD 中，PA⊥平面 ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M 为线段 AD 上一点，AM=2MD，N 为 PC 的中点。

（I）证明 MN ∥平面 PAB；

（II）求直线 AN 与平面 PMN 所成角的正弦值。

10.2016文（19）（本小题满分12分）

如图 5，四棱锥 P-ABCD 中，PA⊥平面 ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M 为线段 AD 上一点，AM=2MD，N 为 PC 的中点。

（I）证明 MN∥平面 PAB；

（II）求四面体 N-BCM 的体积。

11.2017理（19）

如图 6，四面体 ABCD 中，△ABC 是正三角形，△ACD 是直角三角形，∠ABD=∠CBD，AB=BD。

（1）证明：平面 ACD⊥平面 ABC；

（2）过 AC 的平面交 BD 于点 E，若平面 AEC 把四面体ABCD 分成体积相等的两部分，求二面角 D-AE-C 的余弦值。

从题目来看，似乎杂乱无章，经过统计对照分析，就浮现出一些值得关注的规律：

1.以棱柱或棱锥为载体，考查空间中的点、线、面、体的关系。文理题目基本相同，图也相同，2017 年文科和理科的题目所给的条件看似不一样，其实是把文科的问题结论当作理科的一个条件而已。2013 年至2016 年的第 1 问也相同。直得关注的是 2012 年与 2017 年的文理两个问题都相同，可以推测立体几何的重点考查内容基本上就是这些了，因此在复习教学中，让我们有更明确的目标。

2.第 1 问均为传统的推理证明，以直线与平面的平行或垂直为主，平行与垂直呈现出相互间隔的趋势。

3.第 2 问为推理计算，文科求柱体和锥体的体积，且呈相互间隔的趋势；理科为求线面角和二面角，且二者并重。

4.理科第 2 问侧重于利用空间向量解答。

5.如果从解答过程来看，可以发现直线与平面的关系是必不可少的基础，并以此来转化直线与直线、平面与平面的关系。所以在教学上，线面关系应是教学的重中之重。

三、形成规律的原因分析

1.文理题目与图相同，第 1 问也同为推理证明，体现了数学正在向着文理不分科的趋势逐步过渡。传统的逻辑推理文理并重，因为这是数学的基础素养，不应有文理之分，逻辑推理能力应当成为公民的一项基本技能。

2.以棱柱或棱锥为载体，考查空间中的点、线、面、体的关系一直是高考的热点，这类题目既考查多面体的概念性质，又考查空间中线线、线面关系，并将证明和计算有机结合在一起，可以较全面准确了考查学生的空间想象、逻辑推理及计算能力；设计两问，层次递进，由浅入深，能满足不同层次的学生不同偏好的需求，更对基础扎实的学生要求推理与计算全面发展。

3.以平行与垂直为主，突出中学阶段的几何学习重点，以欧氏几何学为重心，反映现实生活中，平行与垂直的组合是最普遍的建筑结构。

4.以直线与平面为主，是因为一维的直线与二维的平面放在三维空间中，有许多种组合方式，最能考查学生的空间想象能力。

5.推理计算的考查，是引导学生深层次地认识数学研究的数量与位置关系是一个分不开的有机整体。一个几何体既有位置的关系，同时又隐藏着数量关系，用通俗的语言来说就是位置关系只是表象，数量关系才是其内涵。

6.理科第二问侧重于空间向量的计算，原因之一就是利用空间向量的运算来解题，能够避免难度较大的空间推理；原因之二是在现代数学研究中，向量是很有活力的一种计算工具，为了让学生的数学思维不落后于数学的发展。向量计算被称为“简单暴力的计算”，不但体现了解决数学问题的程序化、通法化和解析化，而且体现了当前数学还分文理的情况下，对理科生的加强要求。

四、应考策略

1.增强学生的空间想象能力是首要的任务，学生如果过不了这一关，那么在立体几何的学习中就会困难重重。多运动左手对增强空间想象力有一定的帮助。科学研究表明，右脑主要负责音乐、形象、经验、直观等，常说的“创造性思维”也是右脑的产物，但右脑支配着左半身，因此告诉学生活动左手是锻炼右脑的最佳办法，建议学生在日常生活中多动动左手，比如扫地、刷牙、拉灯、洗脸、提水等都可以用左手来做。

2.结合考试大纲，熟悉教材中关于平行与垂直的相关定理，要求学生加强记忆，能理解更好，特别要以线面的平行、垂直的判定为核心，对线线、线面、面面的平行垂直间的关系以及各定理间的相互转化在头脑中经常勾勒演練，如果熟悉这些定理，那么第 1 问的推理证明基本没有困难。

3.熟记一些常见几何图形中与平行垂直相关的结论。

（1）三角形的中位线平行且等于底边一半，既有平行的性质，又有数量关系，可用于计算当中。

（2）平行四边形（包括矩形、菱形、正方形）可实现两组平行线的转换。

（3）等腰三角形底边的中线垂直且平分底边，这个性质既可用于推理又可用于计算，因此最常用。

（4）菱形、正方形对角线有垂直的性质。

（5）垂直关系还可以通过勾股定理的计算来体现。

（6）直角三角形斜边上的中线等于斜边的一半。

4.关于计算问题，文科要加强柱体和锥体的体积计算，特别要注意加强三棱锥的等体积转化意识。理科只要掌握好空间向量的计算，就能轻松地把立体几何题拿下，但是首先也要先能运用垂直的关系建立直角坐标系。

5.适当做一定数量的题目，并在这一版块专注一小段时间，只有专注过的内容，以后才不容易遗忘。

五、解题案例

1.2013年考题的分析与解答过程。

如图 2，三棱柱 ABC-A1B1C1 中，CA=CB，AB=AA1，∠BAA1=60°。

（Ⅰ）证明 AB⊥A1C；

分析：已知 CA=CB，AB=AA1，说明 △ABC 与 △AA1B 都是等腰三角形，而要证明 AB⊥A1C，自然想到运用等腰三角形中线的垂直关系作为突破口，而 △ABC 与 △AA1B 有公共边 AB ，因此先连接 A1B，并在 AB 边上取中点 D，再连接 CD、A1D。如图 7 所示则有

（文Ⅱ）若 AB=CB=2，A1C=，求三棱柱 ABC-A1B1C1 的体积。

分析：由 AB=CB=2，CA=CB 可知 △ABC 为正三角形，可算得 CD=；

由 AB=AA1，∠BAA1=60°可知 △AA1B 为正三角形，可算得 A1D=；

在 △DA1C 中，CD=，A1D=，A1C=，正好有 CD2+A1D2=A1C2，因此可得 CD⊥DA1（這里就是通过勾股定理运算得出垂直关系）。

因此 ⊥平面AA1B1BCD 为三棱锥 C-ABA1 的高。

所以三棱柱 ABC-A1B1C1 的体积 V 有

（这里实现了三棱锥的等体积转化）

（理Ⅱ）若平面 ABC⊥平面 AA1B1B，AB=CB=2，求直线 A1C 与平面 BB1C1C 所成角的正弦值。

分析：由（Ⅰ）知 CD⊥AB，DA1⊥AB

又∵ 面 ABC⊥面 ABB1A1，面 ABC∩面 ABB1A1=AB

∴ CD⊥面 ABB1A1（这是面面垂直转化为线面垂直）

∴ CD⊥EA1 （再由线面垂直转化到线线垂直）

∴ DA，DC，DA1 两两相互垂直

以 D 为坐标原点， 的方向为 x 轴正方向， 为单位长度，建立如图 8 所示空间直角坐标系 D-xyz。

由题设知 A（1，0，0），A1（0，，0），C（0，0，），B（-1，0，0），则，。

设 =（x，y，z）是平面 CBB1C1 的法向量，则

，即，可取 =（，1，-1）

∴ 直线 A1C 与平面 BB1C1C 所成角的正弦值为 （以上为空间向量的运算解决线面角问题）。

2.2017年考题的分析与解答过程。

19.（文）如图 9，四面体 ABCD 中，△ABC 是正三角形，AD=CD。

（1）证明：AC⊥BD。

证明：取 AC 中点 F，连接 DF、BF。

AC⊥平面 DFBAC⊥BD

（这里运用了等腰三角形的中线垂直底边的结论，线面垂直转化为线线垂直）

（2）已知 △ACD 是直角三角形，AB=BD。若 E 为棱 BD 上与 D 不重合的点，且 AE⊥EC，求四面体 ABCE 与四面体ACDE 的体积比。

解：设 AB=2，则 BF=，DF=1，DB=2。

连接 EF，则

（此过程中运用了勾股定理的计算来得到垂直关系，还运用了直角三角形斜边上的中线等于斜边的一半的性质来确定了 E 点为 BD 边的中点，计算三棱锥的体积仍然要用到等体积变换）

19.（理）如图 10，四面体 ABCD 中，△ABC 是正三角形，△ACD 是直角三角形，∠ABD=∠CBD，AB=BD。

（1）证明：平面 ACD⊥平面 ABC。

证明：取 AC 中点 F，连接 DF、BF。

（过程运用了等腰三角形的中线垂直于底边的结论）

设 AB=2，则 BF=，DF=1，DB=2。所以有

BF2+DF2=DB2 DF⊥BF（运用了勾股定理的计算来得到垂直关系）

平面 ACD⊥平面 ABC（由线面垂直转化到面面垂直）

（2）过 AC 的平面交 BD 于点 E，若平面 AEC 把四面体ABCD 分成体积相等的两部分，求二面角 D-AE-C 的余弦值。

解：由条件知平面 AEC 把四面体 ABCD 分成体积相等的两部分，可知 E 点为 BD 的中点。

由（1）可得，以 F 为原点，FA，FB，FD 分别为 x，y，z 轴建立直角坐标系。则

A（1，0，0），B（0，，0），C（-1，0，0），D（0，0，1），E（）

则有

设平面 AEC 的法向量为 ，则

同理可得，设平面 AED 的法向量为 =（x2，y2，z2），则

即二面角 D-AE-C 的余弦值为 （以上为空间向量的运算解决二面角问题）。

总之，立体几何在数学高考中有一定的分量，不但需要学生对空间立体感有较高的认知水平，而且需要学生具有空间推理能力，特别是三棱锥的等体积转化更是要求学生能从不同的角度来识别同一个锥体，它同时也考查了学生的运算能力，对考核学生的综合应用能力有很高的价值。

（责编 卢建龙）