科学推理能力的构成及其考查研究
任唯+刘东方
摘要:从理论上界定科学推理、科学推理能力的内涵,并梳理出科学推理的基本构成类型,概括各推理类型的核心思维过程,为科学推理能力的培养提供理论依据与切入点。从2009~2013年全国高考试卷中选取试题,分析其如何对科学推理能力进行考查,为进一步开发和完善科学推理能力测试工具提供借鉴意义。
关键词:科学推理;能力构成;试题分析;能力考查
文章编号:1005–6629(2015)3–0063–04 中图分类号:G633.8 文献标识码:B
随着青少年的年龄增长,思维发展随之发生变化,逐渐能够通过判断和推理来认识科学原理,进而掌握科学规律。科学推理能力是一种高级思维,对青少年科学思维能力乃至科学素养的形成起到关键作用。自二十世纪六十年代以来,科学推理已成为国外心理学的一个重要研究领域。
1 科学推理能力的界定
在逻辑学中,推理是指根据一个或一些命题得出另一个新判断的思维形式。每一项推理都是由前提和结论两部分组成。已知的判断,是推理的前提;得出的新判断,是推理的结论。正确的前提可以得到正确的结论,反之亦然。科学推理(scientific reasoning)是在推理的基础上得以发展的,最早由皮亚杰在其认知发展理论中提出。
皮亚杰将人类从出生至成人思维质的变化划分为四个阶段:感知运动阶段(0~2岁)、前运算阶段(2~7岁)、具体运算阶段(7~12岁)和形式运算阶段(12~15岁以后),并认为儿童只有进入到形式运算阶段才进入到科学思维的阶段。随着研究的逐步深入,诸多学者对科学推理的概念提出了自己的观点。莱德曼(Lederman)定义科学推理为归纳思维和演绎思维。归纳思维包括概念获得、概念形成、概念图式;演绎思维包括基于创造力、观察、模型建构以及根据经验证据的评价[1]。克拉尔(Klahr)[2]和邓巴(Dunbar)[3]则将科学推理视为问题解决。齐默尔曼(Zimmerman)认为科学推理能力从广义上来说,涵盖了探究学习、设计实验、证据评估、推论思辨、逻辑论证等活动中所需要的一切思维能力和推理技能,这些活动是在形成并逐歩修缮对自然世界和人文社会的各种概念以及理论的认知过程中的关键步骤[4]。斯图西(Stuessy)认为,科学推理能力是个体所拥有的在科学探究过程中观察事物之间关系、作出假设、设计实验检验假设、预言结果出现概率、给出逻辑推断、进行证据评估,最终证明特定结论合理所需要具备的内在逻辑思维形式[5]。汤姆·施莱伯(Tom Schreiber)认为,科学推理能力是建构和评价科学论点且能够作出并证明与科学技术问题相关的决定的能力[6]。
从上述对科学推理以及科学推理能力的界定中可以看出,科学推理的特点是“已知的判断”为科学证据,而得出的“新判断”则是科学结论。因此,在科学研究活动中进行,并根据以科学知识、科学规律以及科学技术手段为支撑的科学证据得出科学结论,是科学推理有别于一般性推理的显著特征。基于此,本研究认为,科学推理是对科学理论进行归纳和演绎的过程,经由发现问题、提出假设、设计实验、证据评估、解释推断等一系列活动,最终使问题得以解决的思维过程。在这一系列活动中所需要的内在思维能力和技能即为科学推理能力,科学推理能力是形式运算阶段开始发展的内在逻辑思维形式。
2 科学推理能力基本构成类型及其考查
为了考查学生的科学推理能力,不同国家和地区开发了测试工具,这些测试工具的理论框架可以作为归纳科学推理构成类型的依据。皮亚杰首先将科学推理分为六种类型,即理论推理、组合推理、比例推理、变量控制、概率与关系推理[7]。1980年,托宾(Tobin)和卡皮(Capie)根据皮亚杰的理论发展出逻辑思维测试工具(Test of Logical Thinking,TOLT),主要是用来测试学生的逻辑推理能力。此测试主要涵盖五种推理类型:比例推理、控制变量推理、组合推理、几率推理和相关推理[8]。
此后,瑞得阳卡(Roadrangka)等人在1982年开发逻辑思维能力的测试工具(Group Assessment of Logical Thinking,GALT),由12个题目组成,主要测试六种推理类型:守恒推理、比例推理、控制变量推理、组合推理、概率推理、相关推理[9]。美国俄亥俄州立大学物理系编制的科学推理测试工具(Lawsons Classroom Test of Scientific Reasoning,LCTSR)涵盖七种推理类型:质量和体积守恒概念、比例推理、变量控制能力、高级变量控制、概率推理、相关性推理、假设演绎推理。虽然这些测试工具对于科学推理的类型划分有差异,但可以从中提炼出在科学学习和研究活动中,科学推理的基本类型包括守恒推理、比例推理、控制变量推理、组合推理、相关推理、概率推理等六种基本类型构成。
高考是我国大型的中学生综合素质测试,具有较高的信效度、必要的区分度和适当的难度,在高考理科试题中蕴涵着诸多科学推理。分析高考试题是如何考查科学推理能力,运用了哪些题型、匹配了哪些试题情境,将为进一步开发和完善科学推理能力测试工具提供借鉴意义。本文以2009~2013年全国各地高考化学试卷为例,举例说明对其中的守恒推理、比例推理、控制变量推理、组合推理四种科学推理类型的考查,分析解题思路和科学推理历程。需要指出的是,我国高考中极少关注相关推理、概率推理这两种推理方式的应用。
2.1 守恒推理
守恒概念研究协作组在《心理学报》上的“守恒概念获得的研究”一文中指出,守恒是在物体外形发生变化时,仍能认识到该物体的某些特性并无改变的能力[10]。守恒推理的核心思维过程为:第一步利用已被证实了的定律、定理分析出在变化过程中始终不发生变化的量或关系;第二步利用这种等量关系推断出要得到的未知量。
例1 (2012年海南卷)将0.195g锌粉加入到20.0mL的0.100 mol·L-1 MO2+溶液中,恰好完全反应,则还原产物可能是( )
A. M B. M2+ C. M3+ D. MO2+
第一步:题干给出明暗两条信息,这是一个氧化还原反应;锌被氧化的物质的量可以通过计算得出。锌失去电子生成氧化产物,MO2+得到电子生成还原产物,溶液中的粒子之间无论发生何种氧化还原变化,溶液始终显中性恒定不变。
第二步:根据这一特征,得失电子数值相等。以参加反应的离子得到电子与失去电子的数目相等为依据推理出还原产物。
2.2 比例推理
比例推理是形式计算的一个重要成分。皮亚杰将比例推理定义为:“能以数学的形式来陈述和阐述函数关系。”我国学者魏金财认为,比例推理是比较不同比(ratio)的能力[11]。比例推理的核心思维过程为:第一步利用题目中信息推断出各量之间的比例关系;第二步能够运用公式、定理等数学关系式将结果正确表达。
例2 (2012年新课标全国卷)铁是应用最广泛的金属,铁的卤化物、氧化物以及高价铁的含氧酸盐均为重要化合物。要确定铁的某氯化物FeClx的化学式,可用离子交换和滴定的方法。实验中称取0.54g的FeClx样品,溶解后先进行阳离子交换预处理,再通过含有饱和OH-的阴离子交换柱,使Cl-和OH-发生交换。交换完成后,流出溶液的OH-用0.40 mol·L-1的盐酸滴定,滴至终点时消耗盐酸25.00mL。计算该样品中氯的物质的量,并求出FeClx中x值。
第一步:根据所给信息推出各量之间的比例关系,酸碱滴定的实质是n(H+):n(OH-)=1:1,因含有饱和OH-的阴离子交换柱,故n(H+):n(OH-):n(Cl-)= 1:1:1,n(Cl-)=0.010mol。
第二步:欲求x,可通过Fe与Cl物质的量之比推出结果,m(Fe)=0.19g;n(Fe)=0.0034mol;物质的量之比推出结果,n(Fe):n(Cl)≈1:3。
2.3 控制变量推理
控制变量推理是对其他变量加以控制,而使需要观察的变量按照特定要求发生变化,据此推理出事物发展变化规律的思维形式。控制变量推理的核心思维过程为:第一步逐一分析出每一因素对结果产生的影响;第二步人为地保持其中一种因素不变,施加另一种因素,观察对结果产生的影响。运用同样的思维方式,保持前面施加的因素不变,使前面保持不变的因素发生变化。当因素很多时,逐一加以控制。第三步综合推断几种因素对结果的影响,得出结论。
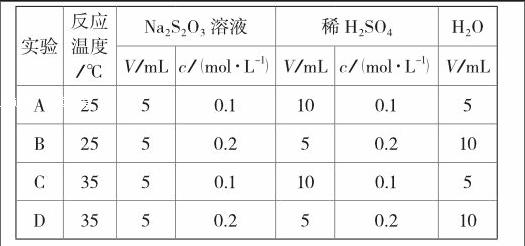
例3 (2009年辽宁、宁夏卷)硫代硫酸钠溶液与稀硫酸反应的化学方程式为:Na2S2O3+H2SO4=Na2SO4+SO2+S↓+H2O,下列各组实验中最先出现浑浊的是( )
本题目选项中给出浓度和温度两因素对化学反应速率影响的信息。
第一步:控制温度变量不变,根据反应物浓度观察、比较反应速率情况。
第二步:在此基础上控制浓度变量不变,再根据温度比较反应速率。
第三步:分别在不同阶段控制温度和浓度变量,发现出现浑浊的变化规律。
2.4 组合推理
把任何单个因素、每两个或每三个结合在一起,就有可能建立所需要的任何关系或分类,这种分类运算和次序关系运算的概括最后发展成为一个组合系统。皮亚杰把同时对多个变量进行推理,能够测定一系列变量中的一个或全部变量的结果,也能测定变量的某种组合的结果称为组合推理[12]。
组合推理的核心思维过程为:第一步由呈现出的多个单一的科学事实及一些隐含的因素,分别推理得到多个单一的科学结论;第二步观察提出的问题,把这些单一的科学结论中一个或几个人为地看成或组合成一个集体,得到新的推理结论。第三步以此方式深入分析、整理,最终使问题得到解决。
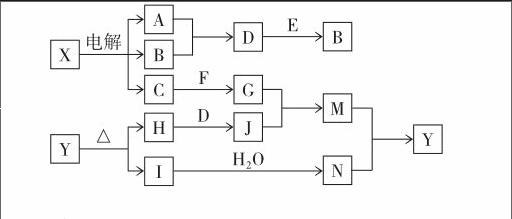
例4 (2012年四川卷)下列框图中的字母分别代表一种常见的物质或其溶液,相互之间的转化关系如下图所示(部分产物及反应条件已略去)。已知A、B为气态单质,F是地壳中含量最多的金属元素的单质;E、H、I为氧化物,E为黑色固体,I为红棕色气体;M为红褐色沉淀。
请回答下列问题:
(1)B中所含元素位于周期表中第 周期,
族。
(2)A在B中燃烧的现象是_____ 。
(3)D+E→B的反应中,被氧化与被还原的物质的物质的量之比是_____ 。
(4)G+J→M的离子方程式是_____ 。
(4)要书写G+J→M的离子方程式,需分别推得物质G和J是什么物质。
第一步:根据题目所给信息F是地壳中含量最多的金属元素的单质,则F是Al;M是红褐色沉淀,故M是氢氧化铁。
第二步:分析物质G。A、B均为气态单质,根据(2)生成AB的反应条件,且D与黑色固体E(二氧化锰)反应生成B,所以A是氢气,B是氯气,D是氯化氢,这样X是氯化物。推得C是强碱,与铝反应生成偏铝酸盐。
第三步:分析物质J。I为红棕色的气体氧化物,则I是NO2,进而Y是硝酸铁。Y受热分解的另一种氧化产物为H:氧化铁;所以J是氯化铁。
第四步:G偏铝酸盐与J氯化铁,二者发生双水解生成氢氧化铝,最终结合离子方程式的书写规范进行书写。可见,正确结论的得出依赖于各因素的综合判断。
3 结论与建议
科学推理能力是思维发展到一定程度后的一种高级思维形式。在美国的2061计划中也强调指出科学的“思维习惯”[15],因此重视对青少年科学推理能力的培养具有十分重要的意义。对于科学推理能力的研究应不仅限于心理学领域,还应更好地与科学教育相结合。在国内科学教育(物理、化学、生物、地理)中,对于青少年的科学推理的相关研究还很少,广大的一线教育工作者还没有对青少年科学推理能力培养形成清晰的认识。科学教育工作者应在深刻理解科学推理能力内涵、构成的基础上,更加深入地挖掘青少年头脑中科学推理能力的形成历程,建立针对科学推理能力的评价框架,确定统一规范的考查量表,以测查青少年能够达到的不同水平,进而更好地培养他们的科学推理能力,提高其科学素养。
参考文献:
[1] Morrell, P. D. & Lederman, N, G. 1998. Students attitudes toward school and classroom science: Arethey different phenomena? School Science and Mathematics,1998,98(2):76~83.
[2] Klahr, D. & Dunbar, K. Dual search space during scientific reasoning. Cognitive Science,1998,12:1~48.
[3] Klahr, D. Exploring science: The cognition and development of discovery processes. Cambridge: MA: MIT Press,2000.
[4] C. Zimmerman. The Development of Scientific Reasoning: What psychologists contribute to an Understanding of Elementary Science Learning? Paper cornmissioned by the National Academies of Science (National Research Councils Board of Science Education, Consensus Study on Learning Science, Kindergarten through Eighth Grade), 2005.
[5] Stuessy, C. Path Analysis; A Model for the Development of Scientific Reasoning Abilities in Adolescents. Journal of Research in Science Teaching,1984,26(1):41~53.
[6][7][9]胡卫平,韩琴,严文法.科学课程与教学论研究[M].北京:高等教育出版社,2007.
[8] RESEARCH REPORT,The structural coherence of students conceptions in mechanics and conceptual change Jose M.Oliva, Centro de Profesorado de Ca′diz, Spain; INT. J. SCI. EDUC.,2003,VOL. 25,NO. 5,539~561.
[10]守恒概念研究协作组.守恒概念获得的研究[J].心理学报,1983.
[11]杨蓉. 4~6岁儿童解决比例推理问题特点及其影响因素的实验研究[D].重庆:西南师范大学,2003.
[12]陈海深.中小学生组合推理能力发展的初步研究[D].桂林:广西师范大学,2008.
[13]邢红军.中学生物理认知水平的模糊判别及其教育价值[J].课程·教材·教法,1997,(7).
[14]周思琪.中学生科学推理能力的比较和分析[D].武汉:华中师范大学,2012.
[15] American Association for the Advancement of Science. Project 2061: Science for all Americans [M].New York: Oxford University Press, 1989.

