4k阶连元幻方的函数构造法
何敏梅,刘兴祥,郭 萍
(延安大学 数学与计算机科学学院, 陕西 延安 716000)
4k阶连元幻方的函数构造法
何敏梅,刘兴祥,郭 萍
(延安大学 数学与计算机科学学院, 陕西 延安 716000)
利用幻阵和函数的基本概念,将函数和幻方结合起来,采用函数方法构造出4k阶连元幻方及其特殊形式始元幻方,并给出证明。
幻方;连元幻方;函数;构造方法
method
函数作为代数学领域的一个重要分支吸引了较多的研究者,并且产生了相当丰富的研究成果。关于幻方的研究成果目前较多,尤其是幻方的构造,现已有多种方法[1-8]。本文主要针对4k阶连元幻方,在充分掌握幻方定义之后运用函数方法构造4k阶连元幻方和始元幻方。
1 预备知识
定义1[9]设F是数域。
1) 矩阵A=aijm×n∈Fm×n,如果矩阵A满足
(1)
则称矩阵A为数域F上的m×n阶行和幻阵,并称Sr为m×n阶行和幻阵A的行幻和。
2) 矩阵A=aijm×n∈Fm×n,如果矩阵A满足
(2)
则称矩阵A为数域F上的m×n阶列和幻阵,并称Sc为m×n阶列和幻阵A的列幻和。
3) 矩阵A=(aij)m×n∈Fm×n,如果矩阵A满足
(3)

(4)
则称矩阵A为数域F上的m×n阶行列和幻阵,并称Sr为m×n阶行列和幻阵A的行幻和,Sc为m×n阶行列和幻阵A的列幻和。
4) 如果矩阵A=(aij)m×m∈Fm×m,矩阵A满足
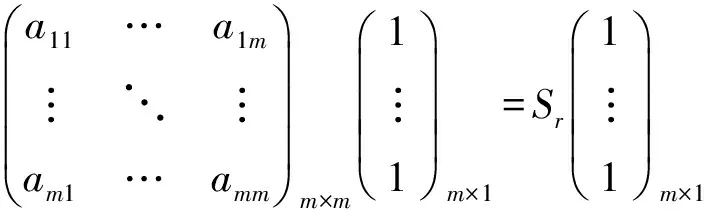
(5)

(6)
③Sr=Sc=S
(7)
则称矩阵A数域为F上的m阶弱和幻方,并称S为m阶弱和幻方A的幻和。
5) 矩阵A=aijm×m∈Fm×m,如果矩阵A满足

(8)

(9)

(10)
则称矩阵A为数域F上的m阶和幻方,并称S为m阶和幻方A的幻和。
定义2[10]矩阵A=(aij)m×m∈{a+1,a+2,…,a+m2}m×m,a∈Z,如果矩阵A满足

(11)

(12)

(13)
④aij≠akl(i≠k或j≠l,i,j,k,l=1,2,…,m)
(14)
则称矩阵A为数域F上的m阶连元和幻方,并称S为m阶连元和幻方A的幻和。
定义3[10]矩阵A=aijm×m∈{1,2,…,m2}m×m,如果矩阵A满足

(15)

(16)

(17)
④aij≠akl(i≠k或j≠l,i,j,k,l=1,2,…,m)
(18)
则称矩阵A为数域F上的m阶始元和幻方,并称S为m阶始元和幻方A的幻和。
性质1[11]设F是数域,矩阵A,B∈Fm×n,∀k,l∈F,若A为m×n阶行和幻阵,B为m×n阶和幻阵,且幻和分别为sA,sB,则矩阵kA+lB是m×n阶和幻阵,且幻和为ksA+lsB。
2 主要结论
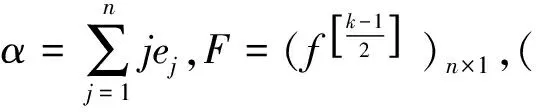
证明先证D满足幻方的条件
1) 当n=4k时由定理知构造出的矩阵
(19)
观察知:矩阵A的各行、各列、主对角线和副对角线的元素都是由1,2,3,…,4k-2,4k-1,4k构成。
矩阵A中:

(20)
(21)
(22)
④Sr=Sc=主对角线和=副对角线和
则称矩阵A为n阶和幻方,简称为n阶幻方。
2) 构造出矩阵
(23)
观察知:矩阵B的各行、各列、主对角线和副对角线的元素都是由0,1,2,3,…,4k-2,4k-1构成。
矩阵B中:

(24)
(25)
(26)
④Sr=Sc=主对角线和=副对角线和。
则称矩阵B为n阶和幻方,简称为n阶幻方。
根据幻方的线性性质可知C=A+nB为n阶和幻方,简称为n阶幻方。
3) 证明矩阵C中的元素是{1,2,…,n2}的全排列。
因为矩阵A中的元素1≤aij≤n,矩阵B中的元素0≤bij≤n-1,则矩阵nB中的元素0≤nbij≤n2-n。所以,矩阵C中的元素1≤cij≤n2,又由始元幻方的定义知∀cij≠ckl,所以矩阵C中的元素是{1,2,…,n2} 的全排列。综上所述,矩阵C是一个n阶始元幻方。

证明先证D满足幻方的条件,其中1)、2)与定理1中1)、2)证明同理。
3)

显然矩阵C为n阶和幻方,简称为n阶幻方。
根据幻方的线性性质可知D=A+nB+C为n阶和幻方,简称为n阶幻方。
4) 下面再证明矩阵D中的元素是{n+1,n+2, …,n+n2}的全排列。
因为矩阵A中的元素1≤aij≤n,矩阵B中的元素1≤bij≤n,则矩阵nB中的元素n≤nbij≤n2,矩阵C中的元素cij=n。所以,矩阵D中的元素n+1≤dij≤n+n2,又由连元幻方的定义知∀dij≠dkl,所以矩阵D中的元素是{n+1,n+2, …,n+n2}的全排列。综上所述,矩阵D是一个n阶连元幻方。
3 结束语
本文在充分掌握了幻方及函数定义之后运用矩阵方法构造4k阶连元幻方以及始元幻方,其他相关结论有待进一步探索。
[1] 刘兴祥,罗云庵.幻方阶数的降与升[J].延安大学学报(自然科学版),1994,13(3):88-92.
[2] 刘兴祥,罗云庵.幻方构造的叠合法[J].延安大学学报(自然科学版),1997,16(2):24-28.
[3] 林淑飞,朱艳伟.构造任意阶幻方的一种新方法[J].云南民族大学学报(自然科学版),2008,17(1):40-44.
[4] 詹森,王辉丰.关于构造高阶幻方的新方法[J].海南师范大学学报(自然科学版),2009,22(3):250-254.
[5] 詹森,王辉丰.构造单偶数阶幻方的四步法[J].海南师范大学学报(自然科学版),2013,26(2):145-151.
[6] 曹燕飞,刘兴祥.构造始元幻方的广义Kronecker积法[J].河南科学,2016,34(7):1022-1025.
[7] 刘兴祥,曹燕飞.4k阶拉丁幻方的构造方法[J].河南科学,2016,34(11):1777-1780.
[8] LIU X X.Generalized Kronecker Product and Its Application[J].Journal of Mathematics Research,2009,1(1):92-97.
[9] 刘兴祥,罗云庵.幻方阶数的降与升[J].延安大学学报(自然科学版),1994,13(3):88-92.
[10] 强春晨.始元幻阵广义Kronecker积的保持性[D].延安:延安大学,2014.
[11] 刘兴祥.幻方构造的叠合法[J].延安大学学报(自然科学版),1997,16(1):24-28.
(责任编辑陈 艳)
TheFunctionConstructionMethodoftheConjunctionMagicSquareMatrix
HE Minmei, LIU Xingxiang, GUO Ping
(College of Mathematics and Computer Science, Yan’an University, Yan’an 716000, China)
Using the basic concept of the function and the magic square matrix.Combine both of them construct the conjunction magic square matrix and the beginning of the magic square matrix by the method of function(n=4k). The prove of them were provided.
the magic square matrix;the conjunction magic square matrix;function;construction
2017-06-14
国家自然科学项目基金资助项目 (61403298);延安大学研究生教育创新计划项目(YCX201719)
何敏梅(1991—),女,陕西宝鸡人,硕士研究生,主要从事矩阵理论研究,E-mail:472454785@qq.com;刘兴祥(1964—),男,陕西渭南人,副教授,硕士生导师,主要从事矩阵理论研究; 郭萍(1994—),女,陕西渭南人,硕士研究生,主要从事矩阵理论研究。
何敏梅,刘兴祥,郭萍.4k阶连元幻方的函数构造法[J].重庆理工大学学报(自然科学),2017(11):211-216.
formatHE Minmei,LIU Xingxiang,GUO Ping.The Function Construction Method of the Conjunction Magic Square Matrix [J].Journal of Chongqing University of Technology(Natural Science),2017(11):211-216.
10.3969/j.issn.1674-8425(z).2017.11.032
O151.21
A
1674-8425(2017)11-0211-06

