基于萤火虫算法的电网节点编号优化
秦煜森,胡 凌,青志明,冯伊娜
(1.国网重庆市电力公司南岸供电分公司, 重庆 401336; 2.重庆渝电监理公司, 重庆 400000; 3.国网重庆市电力公司技能培训中心, 重庆 400053)
基于萤火虫算法的电网节点编号优化
秦煜森1,胡 凌2,青志明3,冯伊娜1
(1.国网重庆市电力公司南岸供电分公司, 重庆 401336; 2.重庆渝电监理公司, 重庆 400000; 3.国网重庆市电力公司技能培训中心, 重庆 400053)
在现代电力系统中,伴随着各类电力电子元件如整流器、逆变器、晶闸管,非线性元件如串并联电容器、同异步电动机、各种无功消耗的家用器件的普及和发展,谐波问题愈加严重,成为电力系统中影响电能质量的关键之一。在电力网络问题的求解中,对节点导纳矩阵的求解,就是对节点编号进行组合优化的过程,因此可以使用群智能算法进行求解。电力网络中的节点编号问题是一个组合优化问题,类似于经典的TSP问题。要求得其最优解较困难,目前已知的编号优化方法包括传统编号优化法和运用萤火虫算法的编号优化法。由程序仿真对比结果可知:将萤火虫算法所找到的最优编号引入的非零元数目比传统算法更少、结果更优。
节点;稀疏技术;TSP问题;萤火虫算法;优化问题
作为清洁方便的二次能源,电能如今已深入人们的生活起居,如何供给优质的电能成为电力工作研究者们所必须解决的问题。在现代电力系统中,伴随各类电力电子元件如整流器、逆变器、晶闸管,非线性元件如串并联电容器、同异步电动机、各种无功消耗的家用器件的普及和发展,谐波问题愈加严重,已成为电力系统中影响电能质量的关键之一。长期以来,以谐波问题为代表的电压或频率的变化一直是衡量电能质量的重要参考。在实现电力供应的初期,存在着早期谐波问题,具体表现为:某些谐波源的元件中的畸变电压和电流干扰电气设备的正常工作。从20世纪50年代开始,由于分析能力和解决手段的限制,谐波问题就伴随着电力系统的发展,且不断增大对电能质量的影响,最终受到世界范围内的普遍关注。这主要是由于电力系统中的非线性元件和直流输电工程设备的增加,随之而来的谐波污染对电力系统环境造成极大影响,因此谐波抑制成为研究的必要,随着用电设备对电能质量要求越来越高,使得谐波问题的解决变得更加迫切[1-10]。
自20世纪60年代开始,智能算法因其优越性,逐渐受到人们的广泛关注。进化算法是具有多个进化形式及原理不全相同的代表性算法,针对不同的领域,解决的方法也不同。
在近十几年来,群智能算法(swarm intelligence algorithm)成为许多研究学者们关注的重点,它是仿生型一类的新型进化算法的总称。在自然界中,群居的各类生物群体可看为一个分布式群系统,群体组织高度结构化。虽然系统里各个体均相对简单,但群体中的关系连接素和群体活动的结构使得个体间能协同工作,完成相对复杂的活动。蚁群优化算法(ant colony optimization,ACO)和粒子群优化算法(particle swarm optimization,PSO)是群智能算法领域的2种典型算法。根据这两类算法的机理,不断地有其延伸算法被发现,其他种群的行为模拟算法也不断被研究者发现,其中就包括萤火虫算法[8-23]。
在电力网络问题的求解中,节点导纳矩阵的求解过程,就是对节点编号进行组合优化的过程,因此可以使用群智能算法进行求解[9,24-38]。
1 节点消去顺序对稀疏矩阵的影响
根据三角分解因子表求解网络方程YV=I的过程,即是对方程进行前代和回代操作的过程。对典型的IEEE9三机9节点系统网络进行说明。
IEEE9三机9节点系统连接如图1所示。

图1 IEEE9系统接线图
对应此系统的节点连线网络如图2所示。

图2 节点网络图
在对此网络进行消去节点运算时,有可能引入非零元素,导致之后的消去过程变得复杂。当消去网络中最外围节点1、2、3时,不会引入非零元素;当消去节点5、7、8时,会使原本无连线的节点间出现1条新增支路,表现在节点导纳矩阵中则为新增1个非零元;当消去4、6、9时,在原网络图中会出现3条新增支路。此过程类似于节点网络中的星网变换过程。
如图3所示,当存在(a)情况时,消去节点j,与之相连的i、j节点将相互连接,网络中产生2条新支路;当存在(b)情况时,消去节点l时,与之相连的i、j均不与k直接相连,网络中将产生2条新支路。如图中虚线所示,表现在节点导纳矩阵中时,将出现新的非零元素。可以引入公式对新增支路数进行求解:

(1)
式中,ΔD表示新增支路数;N为与消去节点相连接的节点数;D代表与消去节点相连节点之间已有的支路数目。

图3 消节点过程的星网变换图
对IEEE9节点的系统进行节点消去操作,若按1—2—3—4—5—6—7—8—9的顺序消去,则将新增3条支路,在节点导纳矩阵的因子表中引入3个非零元素;若按1—4—5—6—2—7—8—9—3的顺序消去,则将新增5条支路,在节点导纳稀疏矩阵中引入5个非零元素。由此可以看出:不同的节点消去顺序对稀疏矩阵的稀疏度影响很大。但若按照1—3—2—5—6—9—4—7—8的顺序进行消去,最终也只增加3条。由此可知:在实际系统中对于网络节点编号的最优方案可以有多种。
2 传统节点编号优化方法
2.1 静态节点编号优化方法
此方法在网络节点连线图中对每一个节点与其他节点相连的支路数进行统计,也即统计该节点的出线度。按照出线度由小到大的顺序对节点进行编号。当存在出线度相同的节点时,随机排列其中的一个在前面。
根据方法的原则可知:在进行因子分解的过程中,对某节点进行消去操作时,只对该节点发出的边的收端节点集中节点对之间的边产生影响,而不影响指向该节点的边,因为在因子分解消去该节点之前的过程中它们已被消去。所以,在计算节点的出线度时,那些已被消去的边在后面不应计入,利用这一思想可以引出节点编号优化中的半动态法。
2.2 半动态节点编号优化方法
此方法也叫作最小度算法。这种方法也是对基于节点的最小出线度进行编号,在编号的过程中区别在于要及时排除已被编号的节点发出的边对未编号节点的出线度的影响。筛选出某个出线度小的节点参与编号,基于因子分解的方法模拟消去该节点,并且只变化网络的结构,其他方面不变。值得注意的是:不对真实的边权进行运算。以此类推,重复上述过程完成最终编号。
2.3 动态节点编号优化方法
当某个节点编号完成后,应立即修正原来的节点连接图并对已消去的边(支路)做标记,被标记的边(支路)不参与之后的模拟消去运算过程。
在程序中,此方法会带来较多的计算量,使操作复杂化。但对比半动态法,该方法的最终编号结果有所改善。
3 萤火虫算法
通过模拟自然界中萤火虫群体的生活特性,从而发明了萤火虫算法,这是一种新兴的群智能优化算法。萤火虫算法目前有两种:GSO(glowworm swarm optimization)的算法与FA(firefly algorithm)。第1种由印度学者Krishnanand等提出;第2种由英国学者Yang提出。从仿生角度看,它们的原理是一样的。
从生物学的角度来说,萤火虫利用特有的闪光信号来定位并吸引异性,从而借此完成求偶交配及繁殖后代。通过模拟自然界中萤火虫的发光行为及机理从而产生萤火虫优化算法。在萤火虫算法中舍弃了萤火虫发光的某些生物学意义,通过寻求主要矛盾,抛弃次要矛盾,充分利用了萤火虫的发光特性从而根据搜索区域寻找伙伴,并向邻域结构内位置较优的萤火虫移动靠近,从而实现位置的优化。
亮度和吸引度是萤火虫算法中2个极其重要的因素。亮度反映萤火虫所在位置的优劣且决定今后的发展方向;吸引度展示出萤火虫移动的距离长短,通过2个因素之间的不断更新换代,最终实现寻得目标函数最优值的目的。
在萤火虫算法中,萤火虫的荧光相对亮度的计算公式可以表达为:
I=I0×e-γrij
(2)
萤火虫的吸引度计算式为:
(3)
萤火虫i、j间移动的位置更新公式为:
xi=xi+β(xi-xj)+α(rand-1/2)
(4)
式(2)(3)(4)中:I0表示萤火虫算法中萤火虫的最大荧光亮度;β0表示萤火虫算法中萤火虫的最大吸引度;γ表示萤火虫算法中光强吸收系数;rij表示萤火虫算法中萤火虫i、j间的距离;xi、xj表示萤火虫算法中萤火虫i和j所处的空间位置;α表示萤火虫算法中的步长因子,一般取0~1之间的随机常数;rand表示萤火虫算法中的随机因子,其服从均匀分布,取值为0~1。
算法中的目标函数为:
(5)
当将萤火虫算法用于网络节点编号优化时,令萤火虫i、j间的距离取为各自所在节点的出线度之差的绝对值。最大荧光亮度与最大吸引度的萤火虫所在节点取为网络外的孤立点(出线度为0)。
萤火虫算法在网络节点优化编号中的实现步骤:
1) 确定萤火虫算法中的参数在网络节点编号问题中各变量之间的对应关系。将m只萤火虫随机分布在n个节点上,根据公式求解所有萤火虫所在位置的相对亮度与相对吸引度,令萤火虫向相对亮度更亮、相对吸引度更大的萤火虫移动;
2) 基于萤火虫算法中萤火虫之间的相对亮度和相对吸引度,对萤火虫位置进行更新;
3) 在对萤火虫算法中萤火虫的位置进行更新的过程中,根据目标函数,计算萤火虫在每个节点消去过后引入的非零元数;
4) 迭代计算,直到迭代完成。
4 算例分析
使用Matlab针对上文介绍的3种传统算法和3种群智能算法编写程序,利用IEEE9节点和IEEE39节点系统的网络拓扑数据进行仿真计算。
使用萤火虫算法和蚁群算法对IEEE9节点系统进行迭代寻优时,程序仿真结果如图4~7所示。

图4 萤火虫算法引入非零元数目

图5 萤火虫算法所找最优编号方案总数

图6 蚁群算法引入非零元数目
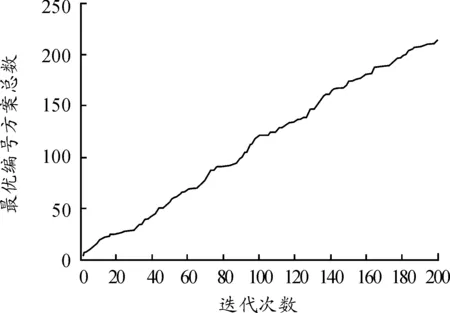
图7 蚁群算法所找最优编号方案总数
程序运行时间对比情况如表1所示。

表1 各算法对IEEE9系统优化所用时间
5 结论
由程序仿真对比结果可知:智能群算法所找的最优编号引入非零元数目比传统算法更少,结果更优;萤火虫算法所找的最优编号方案引入非零元数最少且找到的最优编号方案最多,程序运行时间相对较短。
一般来说,在实际工程运用中,算法越复杂,程序运行时间越长。相较于以前的传统优化算法,群智能算法的优化效果显然更好。基于电力网络节点编号优化问题,在寻优过程中,群智能算法能够找出更多的寻优方案且引入的非零元最少,程序消耗的时间也较短。萤火虫算法在满足最优方案数多的情况下,引入非零元数也最少。
[1] 杨志栋,李亚男,殷威扬,等.±800 kV向家坝—上海特高压直流输电工程谐波阻抗等值研究[J].电网技术,2007(18):1-4.
[2] 姚玉斌,吴志良,王丹,等.电力系统变压器模型分析[J].继电器,2007(24):16-20.
[3] 刘遵义,李向荣,何南强.电力系统谐波阻抗计算[J].华中电力,1994(2):5-8.
[4] 刘启蒙,杨鉴,戈文江.电网节点编号优化算法的改进[J].河北电力技术,2010(1):33-35.
[5] NEZHINSKY A E,VERBEEK F J. Pattern recognition for high throughput zebrafish imaging using genetic algorithm optimization[C]//Proc of the 5th IAPR International Conference on Pattern Recognition in Bioinforma-tics.USA:[S.l.],2010:301-312.
[6] OIDA K,SEKIDO M.ARS:an efficient agent-based routing system for QoS guarantees[J].Computer Communications,2000,23(14):1437-1447.
[7] 王钢,李志铿,李海锋,等.HVDC换流器等值谐波阻抗的计算方法[J].中国电机工程学报,2010(19):64-68.
[8] 杨飞燕,王建全,陈跃辉等.电力系统网络节点编号优化算法的比较研究[J].能源工程,2014(2):23-28.
[9] 吕洋.电网谐波阻抗测量[D].杭州:浙江大学,2010.
[10] 王冠.电力系统谐波分析的元件模型和系统仿真[D].杭州:浙江大学,2003.
[11] 王彦东.电网谐波阻抗特性及测量方法研究[D].成都:西南交通大学,2004.
[12] 刘长平,叶春明.一种新颖的仿生群智能优化算法:萤火虫算法[J].计算机应用研究,2011(9):3295-3297.
[13] MANIEZZO V,COLORNI A. The ant system applied to the quadratic assignment problem[J].IEEE Trans on Knowledge and Data Engineering,1999,11(5):769-778.
[14] PAN Quanke,TASGETIREN M F,LIANG Y C. A discrete particle swarm optimization algorithm for the no-wait flowshop scheduling problem[J].Computers and Operations Research,2008,35(9):2807-2839.
[15] KRISHNANAND K N,GHOSE D. Detection of multiple source locations using a glowworm metaphor with applications to collective robotics[C]/ /Proc of IEEE Swarm Intelligence Symposium,[s.l.],IEEE Press,2005:84-91.
[16] YANG Xinshe. Nature-inspired metaheuristic algorithms[M].[S.l.]:Luniver Press,2008:83-96.
[17] 任志莲.电力系统的谐波分析算法及负荷谐波建模[D].北京:北京交通大学,2009.
[18] 芦晶晶.电力系统谐波分析及程序开发[D].北京:中国电力科学研究院,2005.
[19] 王彦东,李群湛.电力系统谐波阻抗特性及测量方法的探讨[J].电工技术杂志,2004(3):64-67.
[20] 吴笃贵,徐政.电力负荷的谐波建模[J].电网技术,2004(3):20-24.
[21] 丛望,张敬南,吴盼良.电网节点编号优化的一种改进蚁群算法[J].应用科技,2008(12):23-26.
[22] YANG Xinshe. Firefly algorithms for mult-imodal optimization[C]//Proc of the 5th International Symposium on Stochastic Algorithms:Foundations and Applications.USA:[s.n.],2009:169-178.
[23] YANG X S,DEB S. Eagle strategy using lévy walk and firefly algorithms for stochastic optimization[J]. Studies in Computational Intelligence,2010,284:101-111.
[24] 何仰赞.电力系统分析(上册)[M].武汉:华中科技大学出版社,1995.
[25] 何仰赞.电力系统分析(下册)[M].武汉:华中科技大学出版社,1995.
[26] 丁毓峰.精通MATLAB混合编程[M].北京:电子工业出版社,2012.
[27] SHI Yuhui,EHERHART R.A modified particle swarm optimizer [C]//Proc of IEEE International Conference on Computational Intelligence.[S.l.],IEEE Press,1998:69-73.
[28] CARLIER J. Scheduling with disjunctive constraints[J].RAIRO Recherche Operationnelle,1978,12(4) :333-350.
[29] 林海雪,孙树勤.电力网中的谐波[M].北京:中国电力出版社,1998.
[30] 中国电力科学研究院.中国版BPA潮流程序用户手册[z].北京:中国电力科学研究院,2003.
[31] SHARMA V,FLEMING R I,NIEKAMP L.An Iterative Approach for Analysis of Harmonic Penetration in the Power Transmission Networks[J].IEEE Transaction on Power Delivery,1999,6(4):1698-1706.
[32] MANITOBA HVDC research center.EMTDC USer’S guide[Z].Canada:MANITOBA HVDC research center,2004.
[33] 汤涌,张红斌,侯俊贤,等.考虑配电网络的综合负荷模型[J].电网技术,2007(5):34-38.
[34] 李雪梅,张素琴.基于仿生理论的几种优化算法综述[J].计算机应用研究,2009(6):2032-2034.
[35] 张超,魏三强,陈伟.一种基于萤火虫算法的群体动画行为控制仿真设计[J].重庆理工大学学报(自然科学),2017,31(1):100-106.
[36] 范伟,刘峰,徐世军,等.多节点有向无环图优化算法[J].重庆理工大学学报(自然科学),2011,25(12):84-88.
[37] 张兢,史文进,李冠迪,等.无线传感网络中基于RSSI质心定位的改进算法[J].重庆理工大学学报(自然科学),2017,31(3):132-136.
[38] BORMIN H.高性能计算在人工智能中的应用[J].重庆理工大学学报(自然科学),2016,30(8):3-3.
(责任编辑陈 艳)
ResearchesontheGridNodeNumberingOptimizationBasedontheFireflyAlgorithm
QIN Yusen1, HU Ling2, QING Zhiming3, FENG Yi’na1
(1.Nan’an Power Supply Branch Company, Chongqing Electric Power Company, State Grid of China, Chongqing 401336, China; 2.Yudian Supervision Company, Chongqing Electric Power Company, State Grid of China,Chongqing 400000, China; 3.Training Center of Skills, Chongqing Electric Power Company, State Grid of China, Chongqing 400053, China)
In modern power system, with all kinds of power electronic components such as rectifier, inverter, thyristor, nonlinear components such as series parallel capacitor, with asynchronous motor, all kinds of reactive power consumption of popularization and development of household devices, harmonic problem increasingly serious, which has become one of the key to influence the power quality in power system. In solving problems in the electric power network, in view of the node admittance matrix of the solving process, it is the process of combinatorial optimization of node number, so you can use the swarm intelligence algorithm to solve. The node numbering problem in the power network is a combinatorial optimization problem, which is similar to the classic TSP problem. For the optimal solution is difficult, the serial number of known, there are many types of optimization methods, including the serial number of traditional optimization methods and to use the serial number of the firefly algorithm optimization method. Simulation results show that the optimal number of non-zero yuan is less than the traditional algorithm, and the results are better.
nodes; sparse technology; TSP; firefly algorithm; optimization problem
2017-06-28
国家自然科学基金资助项目(51177112)
秦煜森(1982—),男,重庆合川人,硕士,工程师,主要从事电网安全风险管控研究,E-mail:1433969@qq.com。
秦煜森,胡凌,青志明,等.基于萤火虫算法的电网节点编号优化[J].重庆理工大学学报(自然科学),2017(11):198-203.
formatQIN Yusen, HU Ling, QING Zhiming, et al.Researches on the Grid Node Numbering Optimization Based on the Firefly Algorithm[J].Journal of Chongqing University of Technology(Natural Science),2017(11):198-203.
10.3969/j.issn.1674-8425(z).2017.11.030
TM711
A
1674-8425(2017)11-0198-06

