一类植物传染病模型的动力学分析

万槟萁，刘俊利，刘文娟

(西安工程大学 理学院，西安 710048)

一类植物传染病模型的动力学分析

万槟萁，刘俊利*，刘文娟

(西安工程大学 理学院，西安 710048)

研究了一类植物传染病模型，计算了模型的基本再生数．当基本再生数小于1时，模型仅有唯一的无病平衡点，利用Routh-Hurwitz判据和Liapunov函数方法，讨论了无病平衡点的全局渐近稳定性．当基本再生数大于1时，无病平衡点不稳定，模型还存在唯一的地方病平衡点，借助复合矩阵证明了地方病平衡点的全局渐近稳定性．

基本再生数；全局稳定性；Liapunov函数；第二加性复合矩阵

植物不仅为人类的生存提供必要的物质保障，而且对地球上每一个物种而言都是必不可少的. 它为人类提供了生存所必须的氧气、食物和能量. 然而，植物在生长发育过程中受到各种疾病的入侵，导致植物传染病的流行. 为了防治植物疾病灾害，人们在不断地研究植物病的生病机理，传播规律和防治策略. 绝大多数植物病毒依赖于昆虫媒介传播，昆虫媒介主要有蚜虫、叶婵、飞虱和粉虱等. 传染病动力学是对传染病的流行规律进行理论性定量研究的一种重要方法. 从Kermack和Mckendrick在1927年提出经典的SIR仓室模型[1]以来，传染病数学建模已经得到了广泛的研究[2-6]. 文献[7-8]研究了植物病毒的传播特征及流行动力学. 文献[9]考虑了“宿主植物-病毒-媒介-拟寄生蜂”之间的关系并建立了数学模型，为引入拟寄生物的一般生物防治提供了理论依据.文献[10]考虑了具有植物和昆虫两个种群的传染病模型，该文献只对模型进行了数值模拟，分析了在特定参数情况下平衡点的稳定性，对模型的动力学性质并未给出严格的数学证明. 本文的目的是分析此模型的全局动力学行为.

1 模型建立

本文研究的是依赖昆虫媒介传播的植物疾病模型.在自然条件下，植物病毒的侵入一般是被动的，植物病毒侵害多为群体性侵染，因此，文献[10]把植物分为3类：S(t)，I(t)和R(t)，分别表示t时刻易感、染病以及恢复免疫的植物数量.把昆虫分为两类：X(t)和Y(t)，分别表示t时刻的易感和昆虫媒介的数量.并做以下假设：1)植物总数为常数K=S+I+R，由于单位面积上种植的植物的数量一般不变，若植物死亡，可以通过补栽使植物数量保持不变，补栽的新植株都是易感者；2)易感植株仅仅被染病的昆虫介体感染，不考虑易感植物和染病植物间的相互交叉感染；3)昆虫总数为常数N=X+Y.假设μ为植物的自然死亡率系数；m为昆虫的自然死亡率系数；d为染病植物的死亡率系数；γ为植物的恢复率系数；Λ为引入昆虫的密度系数；α,α1分别表示植物、昆虫的饱和率系数；β,β1分别表示植物、昆虫的染病率系数. 建立如下模型：

(1)

则昆虫总数N(t)满足方程

(2)

其中ω=d+μ+γ.

从生物学角度考虑，模型(2)的正向不变集为

易知，模型(2)的无病平衡点为E0(K,0,0)，当R0>1时，模型(2)还存在唯一的地方病平衡点E*(S*,I*,Y*),其中

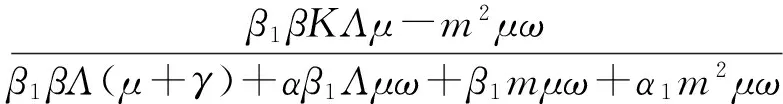
根据文献[11]的第三部分，计算得到模型(2)的基本再生数为

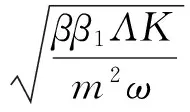
2 无病平衡点的全局渐近稳定性

这一节主要是通过构造Liapunov函数来证明当R0≤1时，模型(2)的无病平衡点E0是全局渐近稳定的.

定理1 当R0≤1时，模型(2)的无病平衡点E0全局渐近稳定；当R0>1时，E0不稳定．

证明模型(2)在E0处的特征方程为

(3)

下面证明当R0≤1时，无病平衡点E0是全局渐近稳定的．

构造Liapunov函数

L(t)=β1ΛI+mωY.

则有

当R0≤1时，L′(t)≤0，当且仅当I=0时，L′(t)=0，由LaSalle不变集原理[12]知，E0是全局渐近稳定的．

3 正平衡点的全局渐近稳定性

本节目的是运用第二加性复合矩阵相关结论和几何方法[13]证明当R0>1时，模型(2)的地方病平衡点E*(S*，I*，Y*)全局渐近稳定.

定理2 当R0>1时，模型(2)的地方病平衡点E*局部渐近稳定．

证明模型(2)在E*处的特征方程为

即

λ3+c1λ2+c2λ+c3=0,

(4)

其中

c1=μ+n1+ω+m+n4,

c2=(μ+n1)(ω+m+n4)+ω(m+n4)-n2n3-n1d,

c3=(μ+n1)[ω(m+n4)-n2n3]-n1(m+n4)d+n1n2n3.

记

显然ni>0(i=1,2,3，4),c1>0.

地方病平衡点E*(S*,I*,Y*)满足方程

因此

c3=(μ+n1)[ω(m+n4)-n2n3]-n1(m+n4)d+n1n2n3=μωm+μωn4-μn2n3+n1ωm+n1ωn4-n1n2n3-n1dm-n1n4d+n1n2n3=(μωm-μn2n3)+μωn4+n1m(ω-d)+n1n4(ω-d)>μωn4+n1m(μ+γ)+n1n4(μ+γ)>0.

c1c2-c3=(μ+n1+ω+m+n4)[(μ+n1)(ω+m+n4)+ω(m+n4)-n2n3-n1d]-(μ+n1)[ω(m+n4)-n2n3]+n1(m+n4)d-n1n2n3=(μ+n1+ω+m+n4)[μω+μm+μn4+n1(ω-d)+n1m+n1n4]+(ω+m+n4)ωn4-n1ωm>(μ+n1+ω+m+n4)n1m-n1ωm=(μ+n1+m+n4)n1m>0.

由Routh-Hurwitz判据[14]可知，特征方程(4)的根均具有负实部．即当R0>1时，地方病平衡点E*(S*,I*,Y*)局部渐近稳定．

与文献[15]中定理2.2的证明类似，得到以下结论.

定理3 当R0>1时，模型(2)是一致持久的．

引理1[15]设开集Ω⊂Rn，对x∈Ω，x→f(x)∈Rn是C1函数. 对方程

(5)

而言，若以下条件满足

(H1) 是单连通区域；

(H2)方程(5)在Ω内存在一个紧的吸引子集E⊂Ω；

(H3) 方程(5)在Ω内有唯一的平衡点x*∈Ω，

则当q<0时，x*在Ω内是全局渐近稳定的，其中

下面证明E*的全局渐近稳定性．

证明由定理3知，模型(2)在区域D内存在一个紧的吸引子集E，从而引理1的条件(H1)-(H3)满足．为证地方病平衡点E*(S*,I*,Y*)的全局稳定性，以下只需证明q<0.

模型(2)的雅可比矩阵为

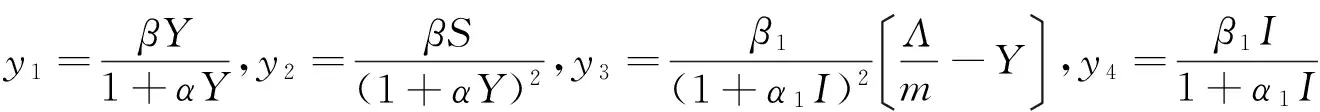
易知yi>0(i=1,2,3,4).

J的第二加性复合矩阵[15]为

J[2]=

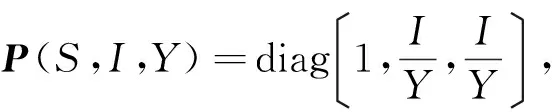
因此矩阵B=PfP-1+PJ[2]P-1可写成分块矩阵

其中

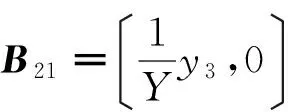
B22=

μ(B)≤max {g1,g2} ，

其中

g1=μ1(B11)+|B12|,g2=|B21|+μ1(B22).

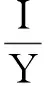
把B22的每一列的非对角线元素取绝对值，然后加到相应列的对角线上得

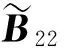
μ1(B22)=

所以

由模型(2)得

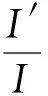
则

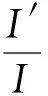
因此

从而

即有

因此引理1的全部条件满足，则R0>1当时，模型(2)的地方病平衡点E*在D内是全局渐近稳定的.

4 结 语

本文研究了一个具有植物和昆虫媒介两个种群的植物疾病模型，得到了模型的基本再生数．此基本再生数完全决定了模型的动力学行为：当R0≤1时，模型(2)的无病平衡点是全局渐近稳定的，即疾病绝灭；当R0>1时，无病平衡点不稳定，疾病持久，唯一的地方病平衡点全局渐近稳定.

[1] KERMACK W O, MCKENDRICK A G. Contributions to the mathematical theory of epidemics [J]. Proc Roy Soc, 1927, (A115): 700-721.

[2] SHI R, ZHAO H, TANG S. Global dynamic analysis of a vector-borne plant disease model[J]. Adv Difference Equ, 2014(1): 1-16.

[3] 赵 绚. 依赖媒介传播的植物病数学模型及分析[D]. 临汾: 山西师范大学, 2014.

[4] 夏丽君. 几类植物病模型动力学性质的研究[D]. 赣州: 赣南师范学院, 2014.

[5] 郭金凤. 若干类植物传染病数学模型的研究[D]. 临汾: 山西师范大学, 2012.

[6] 赵婷婷. 具有经济阈值和物理控制策略的植物疾病模型研究[D]. 西安: 陕西师范大学, 2010.

[7] JEGER M J, MADDEN L V, HOLT J. A model for analysing plant-virus transmisson characteristics and epidemic development [J]. Math Med Bol, 1998, 15: 1-18.

[8] JEGER M J, VAN DEN BOSCH F, DUTMER M Y. Modeling plant virus eqidemics in a plantation-nursery system [J]. LMA J Math Appl Med Biol, 2002, 19: 75-94.

[9] JEGER M J,CHEN Z, POWELL G,etal. Interactions in a host plant-virus-vector-Parasitoid system: Modeling the consequences for virus transmission and disease dynamics [J]. Virus Res, 2011, 159: 183-193.

[10] JACKSON M, CHEN-CHARPENTIER B M. Modeling plant virus propagation with delays [J]. Journal of Computational and Applied Mathematics, 2016, 309: 611-621.

[11] VAN DEN DRIESSCHE P, WATMOUGH J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission [J]. Mathematical Biosciences, 2002, 180: 29-48．

[12] LASALLE J P. The stability of dynamical systems [M]. Philaelphia: SIAM, 1976. 49-78.

[13] LI M Y, MULDOWNEY J S. A geometric approach to global-stability problems [J]. SIAM J Math Anal, 1996, 27(4): 1070-1083.

[14] 马知恩, 周义仓. 常微分方程定性与稳定性方法[M]. 北京: 科学出版社, 2001.

[15] SUN C, LIN Y, TANG S. Global stability for an special SEIR epidemic model with nonlinear incidence rates [J]. Chaos, Solitons and Fractal, 2007, 33: 290-297.

[16] MARTIN R H. Logarithmic norms and projections applied to linear differential systems [J]. Journal of Mathematical Analysis and Applications, 1974, 45(2): 432-454.

Dynamicsanalysisofaclassofplantepidemicmodel

WAN Bin-qi, LIU Jun-li, LIU Wen-juan

(School of Science, Xi'an Polytechnic University, Xi'an 710048, China)

A class of plant disease model was studied, and the basic reproduction number was obtained. When the basic reproduction number was less than or equal to one, there was only the disease free equilibrium. The global stability of the disease-free equilibrium was obtained by the Routh-Hurwitz criteria and Liapunov function methods. When the basic reproduction number is greater than one, the disease free equilibrium was unstable, and there also existed an endemic equilibrium. The global stability of the endemic equilibrium was proved by the compound matrix.

basic reproduction number; global stability; Liapunov function; second additive compound matrix

2017-03-27.

国家自然科学基金资助项目(11101323)；陕西省自然科学基础研究计划资助项目(2014JQ1038)；陕西省教育厅专项科研计划项目(16JK1331)

万槟萁(1991-)，男，硕士，研究方向：微分方程及其应用.

刘俊利(1981-)，女，博士， 副教授，硕士生导师，研究方向：传染病动力学.

O175.1

A

1672-0946(2017)05-0603-04