基于强度折减法与极限平衡法对滑坡稳定性的综合评价

陈思娇

摘要：本文以某滑坡为例分别采用强度折减法和极限平衡法对滑坡稳定性进行分析比较，讨论两种方法的适用性和优缺点，为今后滑坡稳定性分析方法的选择提供依据。

Abstract： This paper takes a landslide as an example with strength subtraction and limit equilibrium method for landslide stability analysis and comparison， to discuss the applicability of the two methods and advantages and disadvantages， and provide evidence for the selection of landslide stability analysis method for the future.

关键词：滑坡；稳定性分析； 强度折减法；极限平衡分析法

Key word： landslide；stability analysis；Strength Reduction Method；Limit Equilibrium Analysis Method

中图分类号：P642.22 文献标识码：A 文章编号：1006-4311（2017）33-0224-03

0 引言

目前计算滑坡稳定性分析中定量计算的常用方法有极限平衡法、强度折减法、极限分析法。极限平衡法是基于刚体理论，假定滑动面后，将滑动土体竖向划分为若干不变形的刚体土条，引入各土条间力，建立和求解力平衡方程。极限平衡法计算简单明了，能快速得到滑坡稳定性系数，在工程中应用最为广泛。但该方法无法反应滑坡的应力应变状态。有限元强度折减法是以弹塑性理论为基础，考虑了滑坡的各项实际材料参数和边界条件，计算结果能直观反映出滑坡的变形位移和破坏过程，更接近于工程实际情况。但目前学术界对滑坡失稳判据也没有统一的认识与定论。本文以某工程中的滑坡为例，分别采用了极限平衡法和有限元强度折减法计算稳定性，并对滑坡稳定性进行综合评价。

1 滑坡基本特征

滑坡体长400m，宽80～200m，平面上呈舌状。地形坡度中后部为10～15°，前缘为公路开挖形成的12m高50°陡坡。该滑坡为覆盖层滑坡，滑体在中、前部较厚，为10～25m，后部较薄3～10m。

根据现场调查及勘探成果揭示，滑体按物质组成不同可以分为两层：上层2～8m为粉质黏土夹少量块碎石，其中粉质黏土约占80%，块碎石主要为粉砂质泥岩，约占20%；下层物质主要为块碎石土夹少量孤石，以粗粒物质为主，粉质黏土含量较少。滑坡滑床为粉砂质泥岩基岩，岩层产状为260°∠16°，滑床顶板坡度与岩层面倾角基本一致。钻孔揭示沿基覆界面存在明显滑带，物质主要为含砾粉质黏土，带宽0.1～0.5m。

调查分析后推断该滑坡是由于前缘阻滑段人工开挖后在持续降雨作用下失稳。根据现场和室内试验成果，岩土体的物理力学参数如表1。

2 基于强度折减法的稳定性分析

2.1 计算模型与破坏标准

计算剖面选择滑坡的主剖面，使用Geostudio软件中的sigma有限元分析模块，计算模型中分层与滑坡物质结构组成一致，从上至下分别为粉质黏土层、碎石土层、滑带土和基岩。

采用Geostudio软件分别计算斜坡在天然和暴雨工况下的稳定性。

工况一：天然状态。天然状态下的荷载主要为岩土体自重。

工况二：天然状态+暴雨状态。除了天然状态下的岩土体自重，还涉及降雨导致岩土体自重增加以及岩土体强度下降的状况。换而言之，工况二必须基于岩土体饱和状态下的容重及抗剪强度指标进行分析和运算。

本次计算强度折减破坏的判据为塑性区域贯通岩土体：首先针对未折减时的塑性区域进行分析运算，然后对滑带土c、Φ折减，随时关注塑性区域的变化趋势。当折减到塑性区域正好在滑坡体中贯通时，所得到的折减系数就是稳定性系数。采用数学运算分析方法分别对天然状态下和暴雨状态下岩土体坡体的稳定性状态进行分析运算。

2.2 计算过程分析

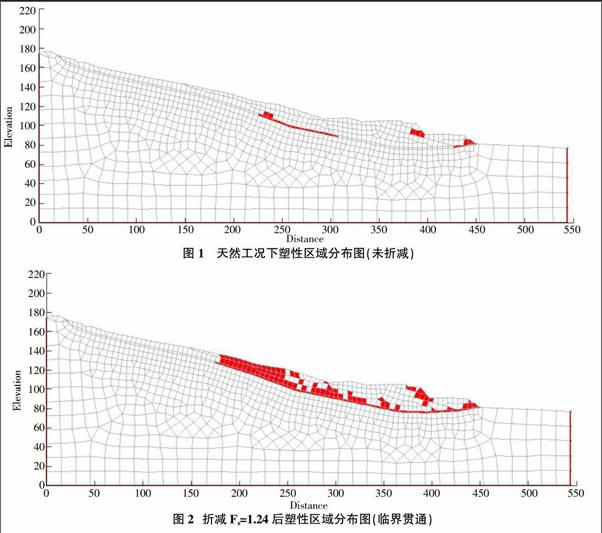
从图1所示天然装填下岩土体的塑性分布情况来看，在强度折减前，斜坡中部的基覆界面和开挖坡脚部位是斜坡塑性分布区，但该区域并不是贯通的塑性带，斜坡相对稳定。强度折减Fs=1.12后，中部逐渐发展成塑性区域，并扩展至中部坡表时斜坡下部塑性区域并未贯通坡脚。继续强度折减，塑性区域沿滑带逐渐贯通至坡脚，中部塑性区域也不断扩大。当折减系数达到Fs=1.24时，塑性区域从坡脚贯通至斜坡中部坡表（图2）。此时折减系数Fs=1.24即滑坡稳定性系数。从塑性区域出现的先后情况来看，滑坡最可能的失稳方式为中部堆积体向坡脚推移式破坏。

采用飽和容重及饱和强度参数对岩土体进行暴雨工况下有限元分析。由图3可见，暴雨工况下斜坡在未折减时，塑性区域已经从坡脚贯通至中部坡表，坡脚和堆积体中部出现大范围塑性区域。可见暴雨工况下斜坡已处于不稳定状态。再进行增大参数的计算，当折减至Fs=0.98时，岩土体塑性区域减小至刚好贯通的临界状态（图4），这时的折减系数Fs=0.98即稳定性系数。

2.3 强度折减法计算结果分析

斜坡失稳破坏判据为塑性区域的贯通，通过基于变形理论的有限元强度折减法计算得到滑坡的稳定性。从塑性区域贯通图可以看出滑坡最可能出现的失稳方式为中部堆积体向坡脚推移式破坏。计算结果表明天然工况下滑坡的稳定性系数为1.24，显然滑坡处于稳定状态；而在暴雨工况下滑坡稳定性系数为0.98，此时滑坡处于不稳定状态。

3 基于极限平衡法稳定性分析endprint

3.1 模型建立

基于传统的极限平衡法分析滑坡堆积体的稳定性状态。用Geostudio软件中slope/w模块，以滑坡主剖面作为计算剖面，分别采用Morgenstern-Price、Janbu、Bishop、瑞典条分法来分析滑坡在天然工况和暴雨工况下的稳定性。

滑坡计算参数沿用表1中的参数。由强度折减法的计算结果可知，在堆积体中部最先出现塑形变形，滑坡可能从中部失稳，而许多现实状况下滑坡基本都是从中部开始。鉴于此，要分析极限平衡法的稳定性，采用两种方法进行计算：一是指定滑坡沿滑带为整体滑面；另一种是指定剪出口位置搜索滑面的方法，计算出滑坡整体滑动面及局部最危险滑动面下的稳定性系数。

3.2 极限平衡法计算结果分析

基于上文所述的计算模型，针对“天然状态”和“天然状态+暴雨状态”下岩土体的稳定性分别进行分析计算，得到表2所示的运算结果。

通过表2可知：天然状态下的主剖面基本稳定，但是在“天然状态+暴雨状态”下，滑坡局部不稳定，并且整体上处于欠稳定至不稳定状态。

4 结语

通过有限元强度折减法与极限平衡法对滑坡稳定性进行了计算，从基于变形理论和基于刚体强度理论两个角度综合评价了滑坡稳定性。强度折减法计算便于分析滑坡的变形破坏特征和滑面形成机理，而极限平衡法计算经过了大量工程实践，其计算的稳定性系数可信可靠，能验证强度折减法失稳判据的选择和计算的结果是否合理。结合两种方法各自的优势，使综合分析的成果更丰富、准确，为滑坡稳定性分析与计算提供了新的思路。

参考文献：

[1]姜玉平，陳征宙，毕港，蒋鑫.基于极限分析法的边坡临界高度及稳定性研究[J].水文地质工程地质，2012，39（2）：43-46.

[2]陈书生.基于强度折减技术的边坡稳定性及其影响因素分析[J].勘察科学技术，2009（3）：3-7.

[3]郑颖人，赵尚毅.有限元强度折减法在土坡与岩坡中的应用[J].岩石力学与工程学报，2004，23（19）：3381-3388.

[4]李红，宫必宁，陈琰.有限元强度折减法滑坡失稳判据.水利与建筑工程学报，2007，15（1）.

[5]栾茂田，武亚军，年廷凯.强度折减有限元法中边坡失稳的塑性区判据及其应用.防灾减灾工程学报，2003，23（3）.endprint