LFM信号检测和参数估计方法研究

曹建光，刘高辉

(西安理工大学，陕西 西安 710048)

LFM信号检测和参数估计方法研究

曹建光，刘高辉

(西安理工大学，陕西 西安710048)

针对分解型分数阶傅里叶变换(FrFT)快速算法与实际工程应用脱节和降低LFM信号参数估计计算复杂度和精度的问题，在分析和研究分解型算法和LFM信号参数估计的基础上，提出了一种基于RAT变换和分数阶域二分法谱校正的LFM信号参数估计的方法，并在FrFT运算中采用量纲归一化。仿真结果表明，本方法可以提高LFM信号参数估计的精度和有效降低计算复杂度，估计精度可以达到CRLB，从而证明了本方法的有效性。

分数阶傅里叶变换；量纲归一化因子；谱校正；参数估计

0 引言

传统的傅里叶变换仅适合平稳信号的研究，分数阶傅里叶变换(FrFT)是一种新兴的时频分析工具，特别适合处理时频耦合信等非平稳信号。LFM信号已经被广泛地应用在电子信息对抗、雷达等多个领域中，对线性调频信号检测和参数估计的研究具有重要的理论和应用价值。

许多研究者对LFM信号参数估计的研究[1-2]都是对离散数据直接用分解型快速算法[3]做FrFT，忽略了对离散数据做FrFT数值计算之前做量纲归一化处理，导致估计值总与理论值有误差。本文采用量纲归一化的分解型快速算法，使得分解型FrFT快速算法能够应用在实际工程中。

在对LFM信号参数进行估计时，文献[4]提出了基于拟牛顿迭代法的两级搜索算法，较好地解决了估计的精度问题，但是该算法是一种迭代逼近算法，运算量偏大且初始值和搜索步长对算法性能的影响比较大。本文提出利用RAT变换[2]首先估计出LFM的调频率，然后利用二分法估计出信号的中心频率，并对搜索得到的峰值点利用谱校正技术[5-6]进行校正，校正得到LFM信号的峰值点，进一步提高LFM信号参数估计的精度，这在精度要求高的场合显得具有重要的价值。

1 FrFT及分解型快速离散算法

时域信号x(t)的FrFT[7]定义为：

(1)

其中p称为FrFT的阶数；Kp(u,t)称为FrFT的核函数，其定义为：

(2)

其中，α=pπ/2为FrFT轴与时间轴的夹角。分数阶傅里叶逆变换的表达式为：

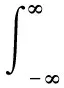
(3)

式(3)说明，信号x(t)可被分解为u域上一组正交LFM基的线性组合，分解型FrFT快速离散算法具有计算速度快、计算精度高的优点，故得到了非常广泛的应用。

2 LFM信号检测和参数估计

2.1离散谱校正技术原理

离散谱校正技术[5-6]是为实现信号参数精确估计而提出来的，此种校正方法的原理是：为了估计信号的频率，对离散化序列x(n)做 DFT，得到序列的离散化频谱模值函数如图1所示。

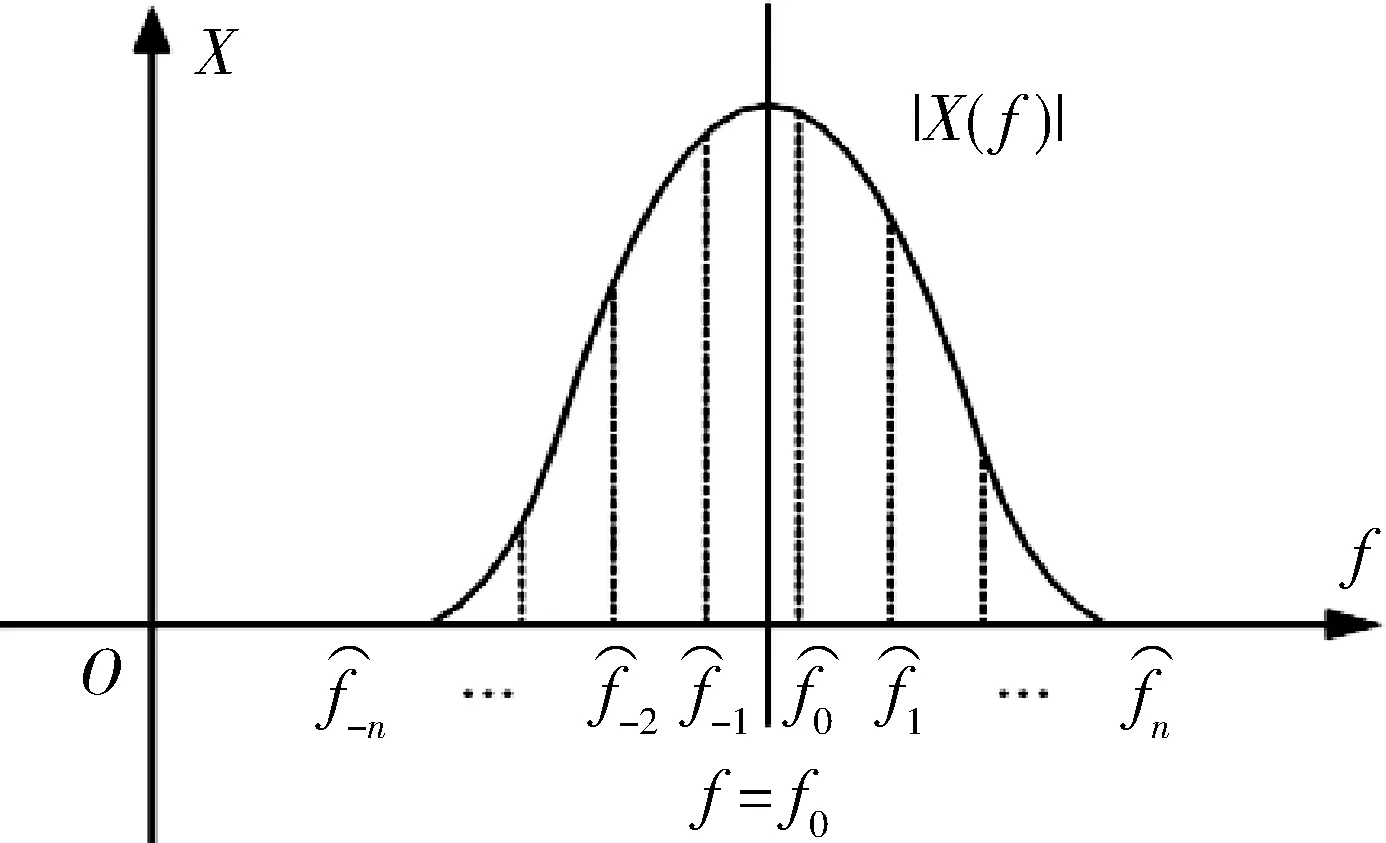
图1 对谐波信号进行加窗截断频率校正

由图1可知，当信号频谱的真实谱峰位置不是准谱线间隔的整数倍情况时，对信号的频率估计会产生误差：

(4)

文献[6]证明，对真实的信号谱峰位置可以结合离散频谱的能量重心原理进行校正恢复，从而得到所估计信号

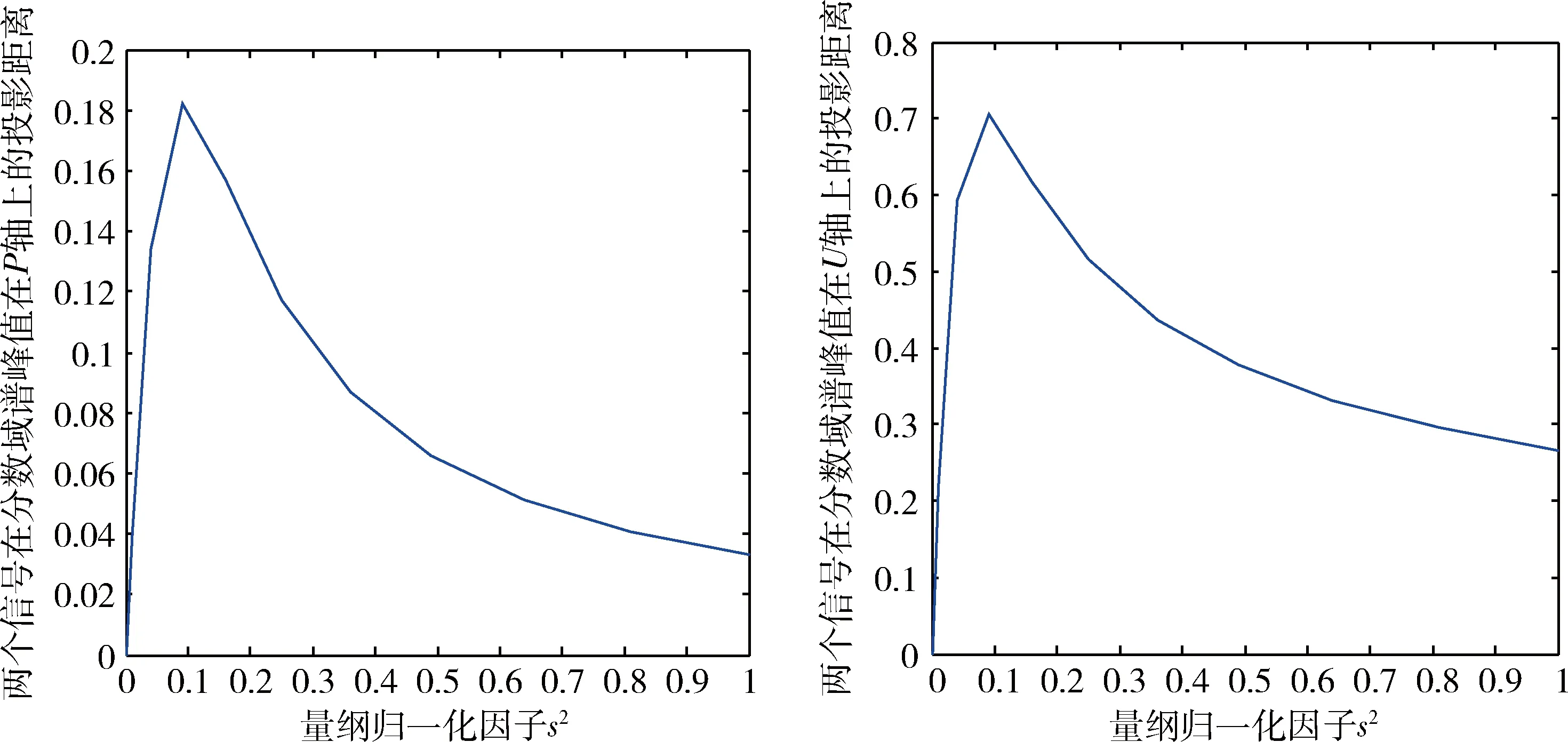
图2 分数域谱峰值在p轴和u轴上的投影与s的关系

的频率大小：

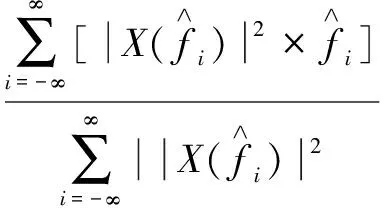
(5)

实际应用中，在频谱能量比较集中的情况下，可以用主瓣内功率谱值较大的几条谱线做近似计算，式(6)便是能量重心法频率校正原理:

(6)

2.2对分解型算法量纲归一化

2.2.1量纲归一化方法

为使分解型FrFT快速算法应用在实际工程中，对实际的离散信号必须进行量纲归一化处理[10-11]，引入具有时间量纲的尺度因子s，并定义新的尺度化坐标：

x=t/s,υ=fs

(7)

对离散数据通过尺度变换进行归一化，关键是要选择合适的时宽tb、宽fb、尺度因子s以及归一化宽度xb，信号的时宽比较容易确定，直接取为观测时间t0，信号带宽fb的选取要能够将信号的全部能量包含在其中。将带宽直接取为采样频率即fb=fs，故可以得到尺度因子s和归一化宽度xb：

s=(tb/fb)1/2=(t0/fs)1/2

(8)

xb=(tbfb)1/2=(t0fs)1/2

(9)

对离散数据按式(7)作尺度变换，则采样间隔变为：

(10)

原来的时域区间[-tb/2,tb/2],经尺度变换后变为[-xb/2,xb/2]。

2.2.2量纲归一化因子的最优化选取

任意两个线性调频信号xr和xl的分数域谱峰值在p轴和u轴上的投影[10]为：

Rp=-arccot(-μlt0/fs)-arccot(-μrt0/fs)/(π/2)

(11)

(12)

取两个线性调频信号xr和xl，xr的高频率μr=12 Hz,中心频率fr=20 Hz，振幅为2，初相位为0；xl的调频率μl=10 Hz,中心频率fl=30 Hz,振幅为2，初相位为0。仿真得到Rp和Ru随量纲归一化因子s2的变化曲线如图2所示。

从图2可以看出LFM信号的谱峰值值与量纲归一化因子s有关系，适当选取s可以使得两个信号的谱峰值增大，这里选取对Rp和Ru取导数求得的极大值所对应的量纲归一化因子s的平均值作为最优的量纲归一化因子。

2.3二分法原理

二分法[12]就是先用DFrFT进行分数域谱峰值初步的搜索，然后对信号在分数域谱峰值二测通过用二分法进行进一步的精确谱峰值搜索。

(1)初步搜索：对所得到的N个离散采样点数据，在分数域内计算N点DFrFT，计算中可用分解型FrFT快速算法实现对连续谱等间隔抽样，搜索LFM信号在最佳阶次下的DFrFT的谱峰值，从而可以实现LFM信号分数域谱峰值所对应的u值初步搜索。

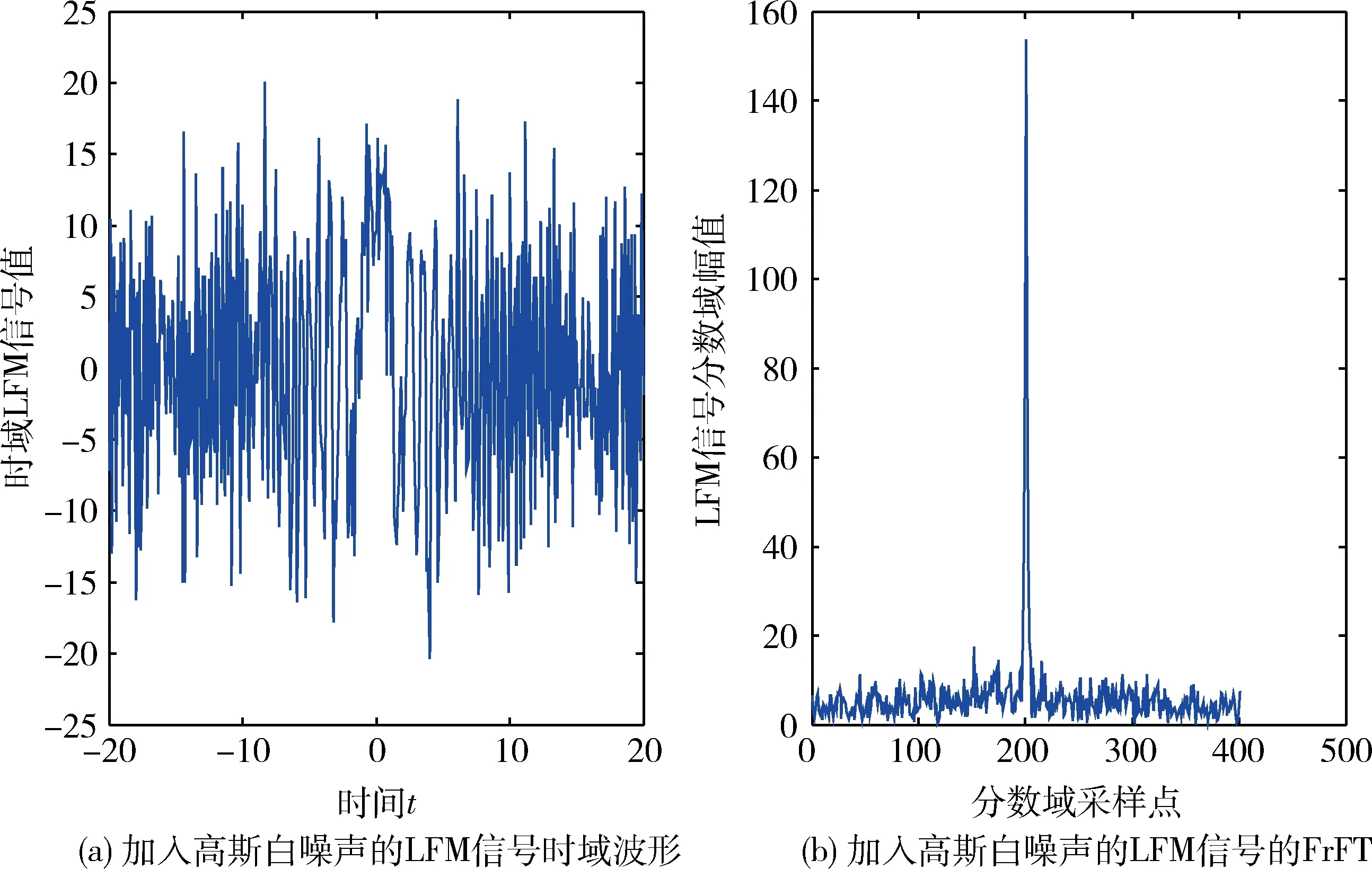
图3 LFM信号时域与分数域图像

(2)精确搜索：对初步搜索得到的信号的分数域谱峰值的最大值点与左右近邻两点做比较，如果此分数域谱峰值点在最大点与第二大点之间，则把这个值作为中间点，计算此点的DFrFT。比如m点是LFM信号的分数域谱峰值点，m-1点为谱峰值点相邻的第二大点，那么此分数域谱峰值点对应的归一化分数阶域u为：

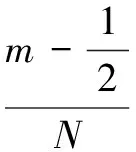
(13)

同时计算峰值点的DFrFT。然后对此点与刚才的左右两点的LFM信号幅度谱做比较，判断真实谱峰值在最大点与第二大点之间，再取其中间点，计算此点的DFrFT，就这样通过反复地计算和比较，通过一次比较计算，搜索得到的信号谱峰值点精度就会增大2倍。

2.4利用RAT变换和分数域二分法谱校正的LFM信号参数估计

2.4.1利用RAT并结合谱校正技术对LFM信号调频率估计

利用RAT对LFM信号的调频率进行估计，基本原理为：假设LFM信号为：

x(t)=a0[exp[jπ(f0t+μ0t2+φ0)],-∞≤t≤+∞

(14)

其中a0、f0和μ0分别为线性调频信号的幅值、中心频率以及调频率，得到LFM信号的模糊函数为：

(15)

对式(15)取模，然后对它做过原点直线ξ=kτ上的radon变换，取不同的直线斜率k，得：

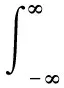
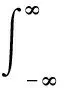
(16)

由式(16)知：k=k0=μ0时，得目标函数η(k)的最大值。通过此性质，可对η(k)进行谱峰位置搜索得出LFM信号的调频率估计值，用公式表示为：

(17)

2.4.2基于FrFT的LFM中心频率、幅值和初相位估计原理

由图3可以知道，LFM信号在时域分析比较困难，而在分数域LFM信号在最优变换阶次下则表现出很好的能量聚集特性。

(18)

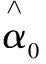
(19)

(20)

2.4.3本文提出方法的具体实现步骤

本节将谱校正技术分别引入模糊域和分数阶傅里叶域，实现信号参数的超分辨率估计，进而给出基于RAT和FRFT谱校正估计LFM方法的实现步骤如下：

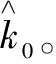
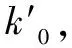
(21)

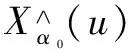
(22)

由式(22)估计出信号的中心频率：

(23)

根据上面估计出的调频率和中心频率，由式(24)可以得出LFM信号的幅值和初相位：

(24)

3 仿真实验

设一单分量LFM信号，参数取为：a0=1.5，f0=100 Hz，μ0=10 Hz，φ0=π/3，观测时间取T=6 s,噪声取加性高斯白噪声，信噪比SNR=[0～15 dB]，得LFM信号参数估计值的均方误差(MSE)随信噪比变化特性曲线如图4所示。

4 结论

本文针对FrFT分解型快速算法与实际工程应用脱节和降低LFM信号参数估计计算复杂度和精度的问题，提出了一种基于RAT变换和分数阶域二分法谱校正的LFM信号参数估计的方法，把二维的搜索运算转化为2次一维的搜索运算，并在FrFT运算中采用量纲归一化和进行谱峰值的校正。分析和仿真结果表明，本文提出的基于RAT变换和分数阶域二分法谱校正的LFM信号参数估计精度有所提高。

[1] 卢慧英,朱灿焰.基于FRFT的多LFM信号的分离及参数估计[J].通信技术,2011,44(9):32-35.

[2] 罗蓬. 基于分数阶Fourier变换的非平稳信号处理技术研究[D].天津:天津大学,2012.

[3] PEI S C, YEH M H, TSENG C C. Discrete fractional fourier transform based on orthogonal projections[J]. IEEE Transactions on Signal Processing, 1999, 47(5):1335-1348.

[4] 陈蓉,马菊红. 基于拟牛顿迭代的分数阶Fourier变换最佳阶次的搜索方法研究[J]. 江苏科技大学学报(自然科学版),2015,29(1):81-84,89.

[5] 焦新涛.离散频谱分析中的连续谱校正技术[D].汕头：汕头大学，2001.

[6] 丁康，汪利旗.离散频谱的能量重心校正法[J].振动工程学报，2001,14(3):354-358.

[7] 刘高辉,曹建光.一种快速时变衰落信道估计方法研究[J]. 无线互联科技,2017(2):106-110.

[8] OZAKTAS H M, ARIKAN O, KUTAY MA, et al. Digital computation of the fractional fourier transform[J]. IEEE Transactions on Signal Processing, 1996, 44(9):2141-2150.

[9] OZAKTAS H M. The discrete fractional fourier transform[J]. IEEE Transactions on Signal Processing, 2000,48(5):1329-1337.

[10] 刘锋,徐会法,陶然. 分数阶Fourier变换中量纲归一化因子的选取[J]. 系统工程与电子技术,2011,33(2):237-241.

[11] 赵兴浩,邓兵,陶然.分数阶傅里叶变换数值计算中的量纲归一化[J]. 北京理工大学学报,2005,25(4):360-364.

[12] 冬海,周海中. 基于二分法峰值的频率搜索算法[J]. 电子信息对抗技术,2013,28(1):10-12,35.

[13] KAY O, BOUDREAUX-BARTELS G E.Fractional convolution and correlation via operator methods and an application to detection of linear FM signals[J]. IEEE Transactions on Signal Processing,2001,49(5):979-993.

曹建光(1988-)，通信作者，男，硕士研究生，主要研究方向：先进导航技术。E-mail:1279777638@qq.com。

刘高辉(1968-)，男，博士，副教授，硕士生导师，主要研究方向：信号与信息处理和通信集成电路设计。

The research on the detection and parameters estimation of LFM signal

Cao Jianguang, Liu Gaohui

(Xi’an University of Technology, Xi’an 710048, China)

Aiming at the problems that the decomposition FrFT fast algorithm is separated from the actual engineering application and how to reduce the computational complexity and accuracy of LFM signal parameter estimation, by analysing and researching decomposition algorithm and the estimation of LFM signal parameters , this paper presents a method based on RAT transform and using division combining spectral correction technique in fractional domain to realise estimation of LFM signal parameters,which uses the dimensional normalization during the calculation of FrFT.The simulation results show that this method can improve the precision of the estimation of LFM signal parameters and reduce the computational complexity, whose precision can reach CRLB.The simulation results prove that this method is effective.

fractional Fourier transform; dimensional normalization factor; spectrum correction;parameter estimation

TN911.23

A

10.19358/j.issn.1674- 7720.2017.22.026

曹建光，刘高辉.LFM信号检测和参数估计方法研究J.微型机与应用，2017,36(22)：99-102.

2017-03-31)