射频功率放大器幂级数模型的系统辨识与实现

仝 野

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

射频功率放大器幂级数模型的系统辨识与实现

仝 野

(南京邮电大学 通信与信息工程学院，江苏 南京210003)

幂级数模型是描述无记忆功率放大器的一个常用模型，系数辨识是准确建立模型的关键因素。通过对功放非线性等特性的研究，探讨辨识幂级数模型的最小二乘算法与卡尔曼滤波算法，对功放的实际应用具有一定的指导意义。研究了基于最小二乘法与卡尔曼滤波算法的射频功率放大器幂级数模型的参数估计方法，进行了相应的数值仿真实验，结果显示：最小二乘算法具有计算简单与容易实现的优点，而卡尔曼滤波算法计算量大，原理复杂，但当幂级数阶数有限时，随着迭代次数的增加，估算的准确度会更高。

射频功率放大器；幂级数模型；系统辨识；最小二乘算法；卡尔曼滤波算法

0 引言

射频功率放大器是现代无线通信体系中实际操作用到的基本器件之一，也是系统非线性的重要出处[1]，提高其线性性能是一项艰巨任务。由于实际需求，功放要工作在非线性区域才能使信号得到足够的放大，导致了以前的小信号分析理论不能满足现实的需要，特别是在射频微波技术方面呈现的问题非常突出，这是目前亟待解决的重要难题。

要研究射频功率放大器，首先要对功放进行数学建模。行为模型是功率放大器模型的一种重要类型，其又可以细分为：无记忆行为模型和有记忆行为模型[2]。幂级数模型是描述无记忆射频功率放大器的一个简单的常用模型。本课题通过对射频功率放大器幂级数模型的分析，探讨了辨识功放幂级数模型系数的几种常用方法，对于功放的实际应用具有重要的指导意义。此外，幂级数模型也是一些功放记忆模型的基础，如记忆多项式模型，因此掌握好幂级数模型对复杂模型有极大帮助。

1 PA幂级数分析模型

幂级数模型是描述无记忆功放最常用的分析模型，这里对它的一般形式进行归纳。使用幂级数对功放建模时，功放的输入信号与输出信号可以用下面的幂级数描述[3]：

(1)

式中，ci表示模型系数。幂级数模型特色是模型系数ci能够表示功放输出信号幅度的失真，进一步能够推算系统的载波互调功率比，对于一般的非线性功放，只需取前三阶即可满足实际要求。当ci取复数时，幂级数模型不仅可以表示功放信号幅度变化，也能表示相位变化。

2 PA幂级数模型的系数辨识算法

2.1最小二乘算法

根据Weierstrass定理进行函数逼近，解析函数G(x)能够用一个阶次足够大的多项式近似[4]，所以可以用下面公式描述：

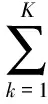
(2)

式中ck表示模型系数，x(n)表示输入信号，f(n)表示输出信号，K为非线性的阶数。

但在实际应用时，通常并不直接采用式(2)，而是将其变形为:

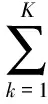
(3)

幂级数模型可以方便地用最小二乘算法辨识出其中的参数[5]。经实际测量可得功放的N对输入、输出数据值，令输入信号序列记为x0,x1,x2,…,xN，输出信号序列为f0,f1,f2,…,fN,则输入、输出矩阵分别为:

(4)

FN=(f0,f1,…,fN)T

(5)

将模型中的参数记为：

C=(c1,c2,…,ck)T

(6)

则式(1)可表示为如下矩阵方程:

FN=XN·C

(7)

(8)

其中上标H用来表示矩阵的共轭转置。

2.2卡尔曼滤波算法

在用卡尔曼滤波算法辨识功放的参数时，首先要对系统进行建模。通常情况下，除了奇数阶失真分量，其他失真分量均可用滤波器滤除，因此为了简化起见，只考虑奇数阶分量。功放奇数阶幂级数数学模型表达式为：

(9)

其中M为非零自然数，b2i-1表示第2i-1个模型系数，则模型的阶数为2M-1。奇数阶幂级数模型形式简单，系数容易识别。

如果令f2i-1(n)=s(n)s(n)2i-2，则式(9)可以改为：

(10)

将式(10)变换成矩阵形式：

x(n)=[Fn]Tb

(11)

其中[b]M×1=(b1,b3,…,b2M-1)T是模型系数矢量。

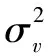
y(n)=[Xn]Th+v(n)

(12)

其中h=(h(0),h(1),…,h(Lh-1))T，[Xn]Lh×1是矩阵[X]Lx+Lh-1的第n行所有元素组成的列向量，其中Lx表示功放输出序列长度，Lh表示有限长单位脉冲响应的长度，X具体描述为：

(13)

由式(13)知，[Xn]Lh×1=([Fn]Tb,[Fn-1]Tb,…,[Fn-Lh+1]Tb)T为矩阵形式。

若令：[Fn]MLh×1=([Fn]T,[Fn-1]T,…,[Fn-Lh+1]T)T，则有：

Xn=(I⊗b)T·Fn

(14)

其中符号“⊗”表示克罗内克积，那么输入输出关系可以写为：

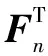
(15)

称hb为扩展信道，并可知hb=h⊗b。由于射频功放的非线性特性和信道的传输特性在一段时间内是不变的，那么扩展信道具有时间不变性，即：hb(n)=hb(n-1)。

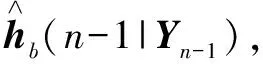
步骤1 卡尔曼滤波器估计扩展信道

时间更新：

(16)

P(n,n-1)=P(n-1)

(17)

状态更新：

(18)

A(n)=Φ(n)P(n,n-1)ΦH(n)+Q

(19)

κ(n)=P(n,n-1)ΦH(n)A-1(n)

(20)

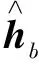
(21)

P(n)=(I-κ(n)A(n))P(n,n-1)

(22)

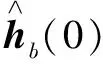
3 辨识算法的实现与比较

本节主要介绍利用最小二乘算法与卡尔曼滤波算法对特定的功率放大器幂级数模型进行系数识别。

3.1基于最小二乘算法的辨识实现

对功放的实际输入输出数据进行测量，得到此功放的一组观测数据，通过MATLAB软件仿真，可得到此功率放大器的输入-输出幅度变化图，如图1所示。

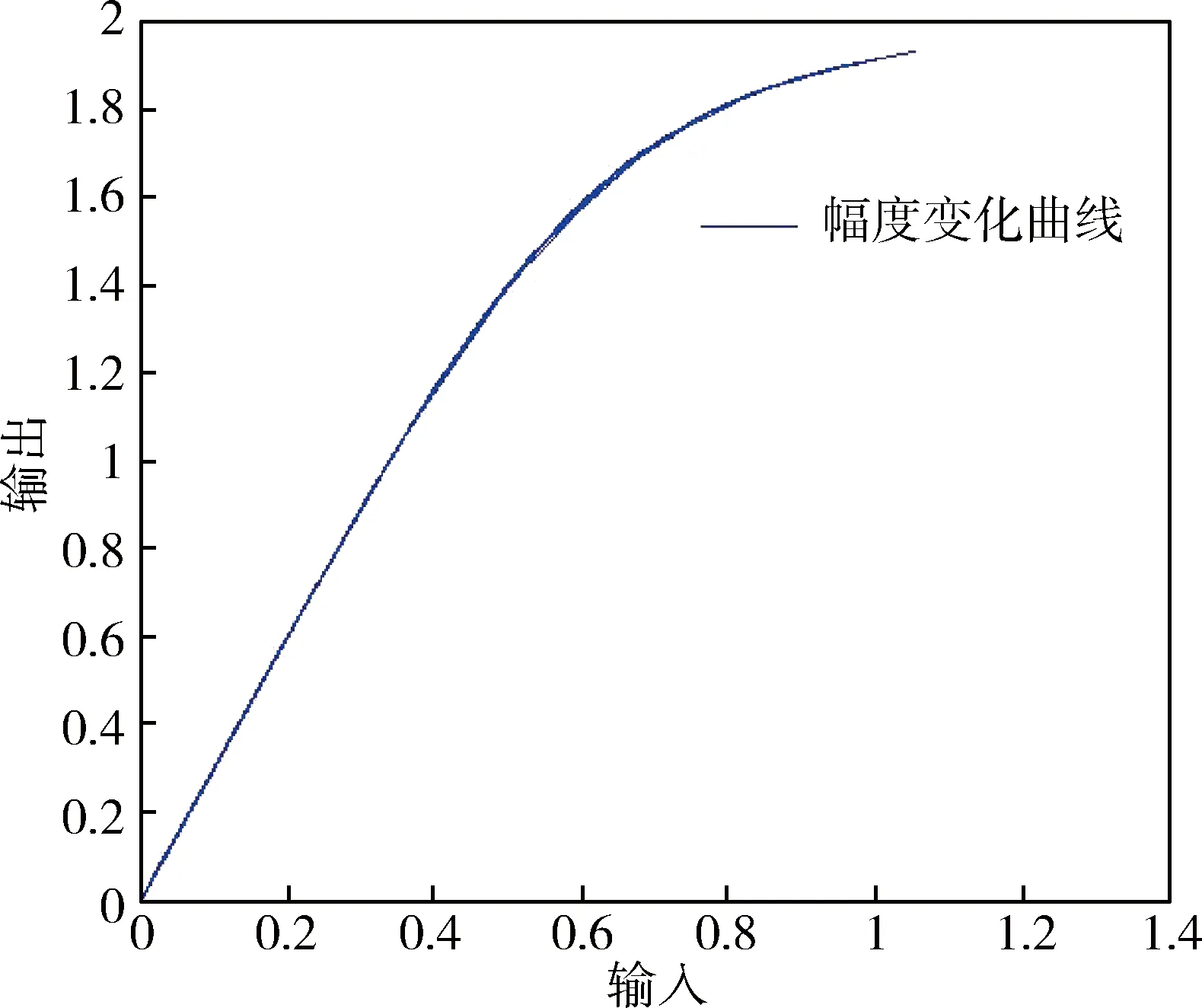
图1 功放输入-输出幅度变化图

功放幂级数模型表达式简便，易于通过算法识别系数，且能够直观地表示非线性特性，公式为：

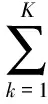
(23)

式中，K为非线性的阶数。

幂级数模型中经常使用的是低阶模型，简单方便，不足是拟合准确度有限，但是若使用很高阶数的模型，功放的输出信号很可能出现“振荡”[6]。所以，要想提高模型准确度，不能简单增加幂级数阶数。图2是选取不同阶数的幂级数进行仿真的结果。

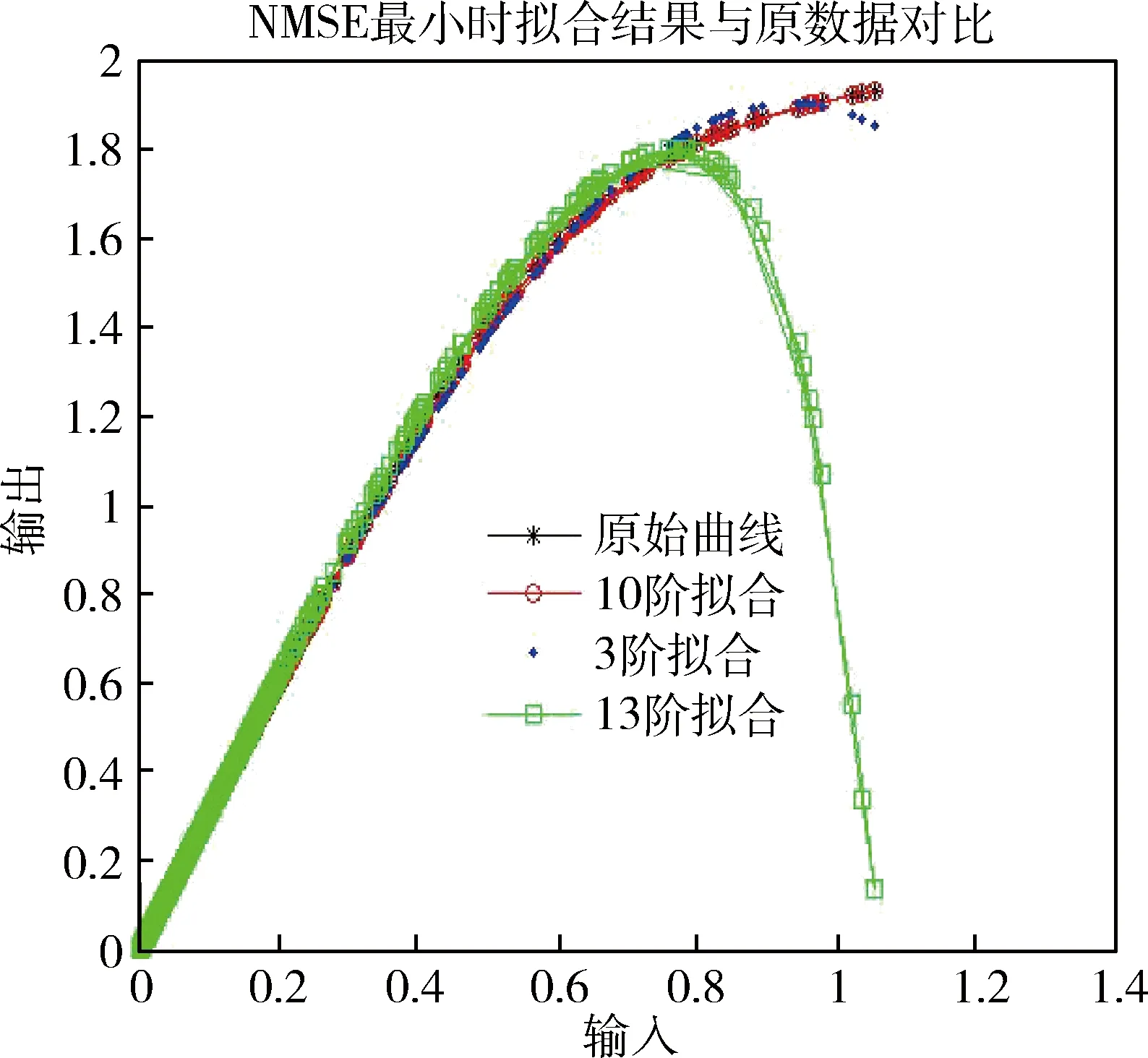
图2 不同阶数的幂级数模型拟合结果

由图2可以看出阶数为10时，模型的拟合效果最优。

在模型阶数为10时，利用最小二乘算法得到的模型系数如表1所示。

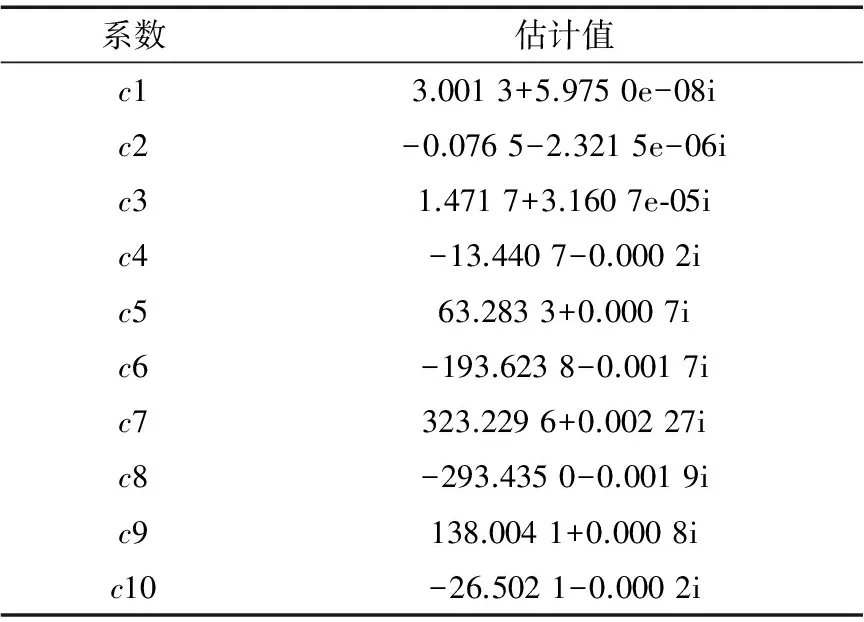
表1 模型系数

上面模型的计算结果通常使用归一化均方误差、误差矢量幅度等指标来评价其精度。本文选用NMSE来评价无记忆功放模型的计算精度，具体定义如下：

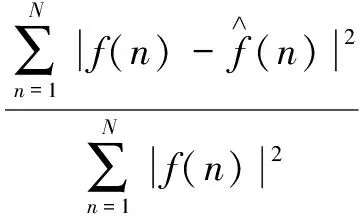
(24)

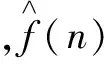
图3是在不同阶数下，采用NMSE功放输出的拟合的精度曲线，横轴为阶数，纵轴为对应的NMSE值。

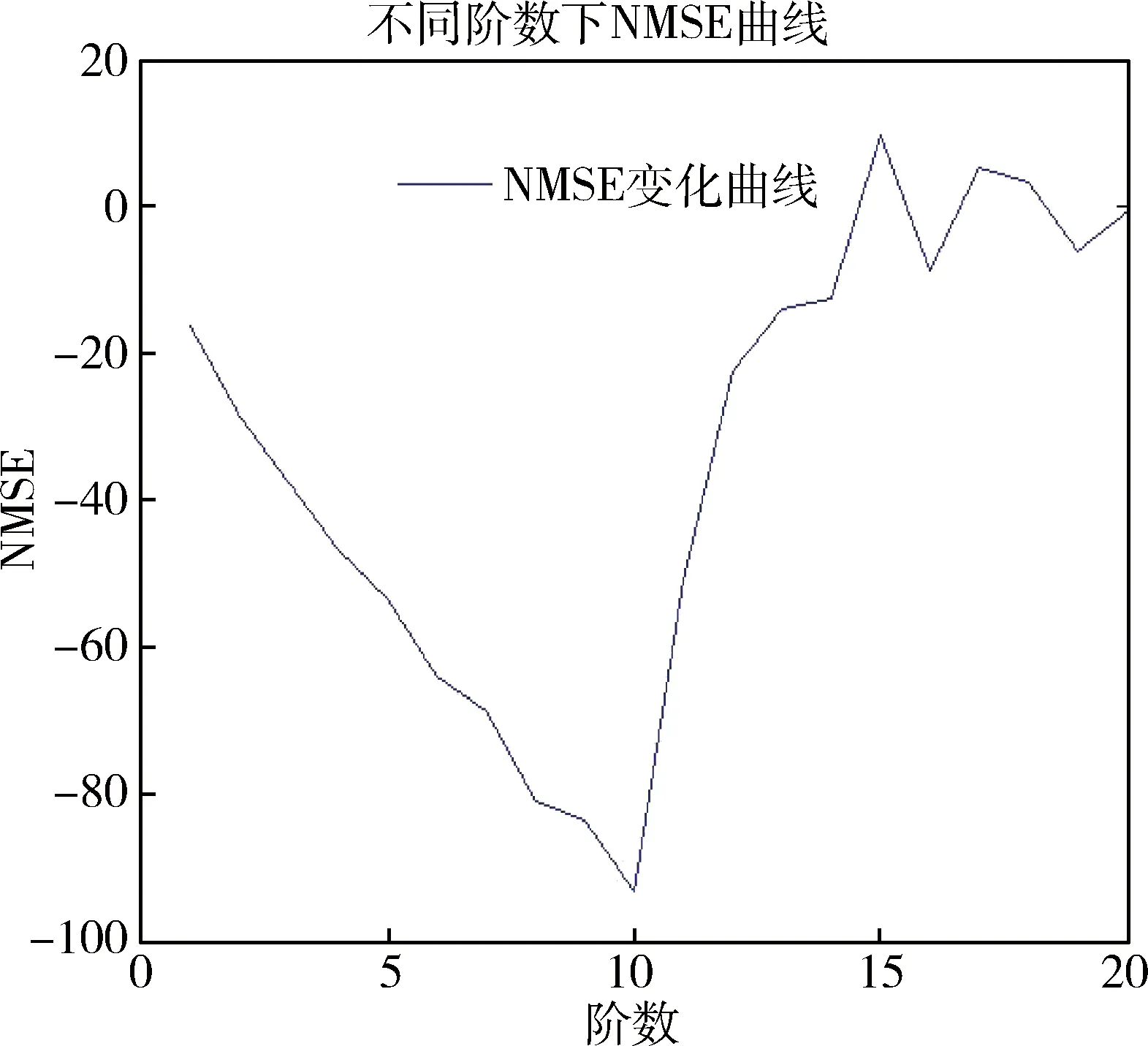
图3 不同阶数下NMSE曲线

从图3中可以清楚地看到阶次在20以下的各阶次中，阶数为10时，NMSE值最小，验证了模型(23)阶次取10时拟合精确度较高。

3.2基于卡尔曼滤波算法的辨识实现

OFDM是无线通信系统中一种传输技术，利用多信道多载波提高系统频谱利用率，因采用多个子载波技术而能够抗多径衰弱。基于IEEE 802.11a协议的OFDM系统应用十分广泛。由于支持IEEE 802.11a协议的无线局域网主要应用于室内，其信道是一个慢衰落信道，故而在一定时间内信道传输特性为恒定的。由IEEE 802.11a协议可知，OFDM的前导序列既有长序列也有短序列(10短2长)，其中长序列长度为160。

针对IEEE 802.11a协议，采用16-QAM调制的OFDM系统进行MATLAB仿真。使用室内经验无线传输信道模型h(n)=0.996 0δ(n)+0.062 8δ(n-1)+0.007 9δ(n-2)，功放模型阶数为5阶，功率放大器幂级数模型系数如表2所示。依照协议产生长训练序列，形成观测集。

表2 功率放大器幂级数模型系数

扩展信道hb得到后就可以根据式(15)计算得到功放模型系数b。表3是第1 024次迭代估算出的模型系数值与真实值的比较，由此表可以看出随着信噪比升高估算值越来越逼近真实值。

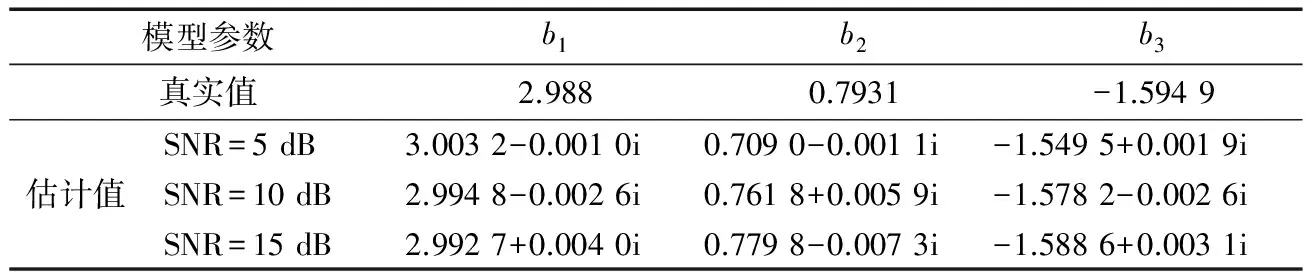
表3 估计值与实际值的比较

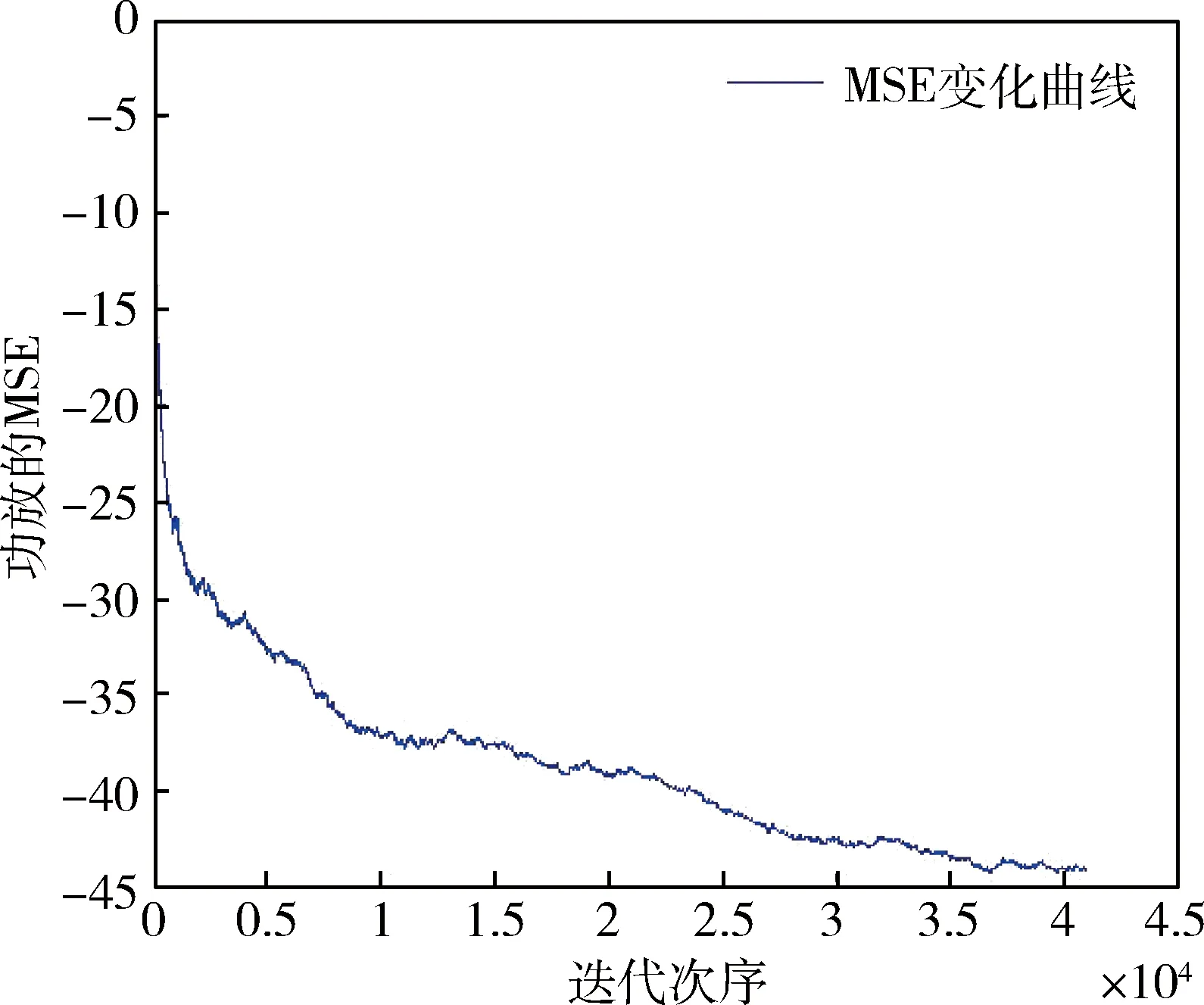
图4 扩展信道均方误差曲线

4 结论

通过以上两节对实例的实际辨识可以得出，功放幂级数模型能够方便有效地用最小二乘算法辨识出其中的参数，模型简单，计算方便，实现起来也相对容易，幂级数模型中经常使用的是低阶模型，简单方便，不足是拟合准确度有限，但是若使用很高阶数的模型，功放的输出信号很可能出现“振荡”。所以，要想提高模型准确度不能简单增加幂级数阶数。

采用卡尔曼滤波算法的系统模型相对复杂，需要借助信道实现幂级数模型系数的估算，计算量大，原理理解也相对困难，但当幂级数阶数有限时，随着迭代次数的增加，估算的准确度也在升高。系数估算的准确度也受信噪比影响，随着信噪比升高，估算值也越来越逼近真实值。

综上所述，上述两种辨识方法各有其优缺点，应根据实际情况择优选取。

[1] 郭阳. 高效射频功率放大器数字预失真关键技术研究[D]. 成都: 电子科技大学, 2011.

[2] SABAGHI C, HADIANAMREI S, RAHNAMA M, et al. Using LDMOS transistor in class-F power amplifier for WCDMA applications[J]. International Journal of Communications, Network and System Sciences, 2011, 4(10)： 662-666.

[3] 祝乐芳. 功率放大器的非线性预失真技术的研究[D]. 沈阳: 沈阳理工大学, 2012.

[4] 高金辉,苏明坤,李迎迎.基于ADS仿真的射频功放设计[J]. 河南师范大学学报(自然科学版),2011,39(6): 48-50.

[5] 闫博. 基于ADS的射频功率放大器设计与仿真[D]. 长沙: 国防科学技术大学, 2010.

[6] PARK C. Experimental investigation of differential line inductor for RF circuits with differential structure[J]. International Journal of Maritime Information and Communication Sciences,2011,9(1):11-15.

2017-04-19)

仝野(1993-)，男，硕士，主要研究方向：通信与信号处理。

System identification and realization of RF power amplifier based on power series model

Tong Ye

(College of Communication amp; Information Engineering, Nanjing University of Post amp; Telecommunication, Nanjing 210003, China)

The power series model is a common model for the description of the memoryless power amplifier, and the coefficient identification is the key factor to establish the model. Through the study of the nonlinear characteristics of the amplifier, the research on the least square algorithm and Kalman filtering algorithm with power series model has some guiding significance on the practical application of the power amplifier. This paper studies the estimation method of radio frequency (RF) power amplifier power series model parameters based on least square algorithm and Kalman filtering algorithm. We conduct the corresponding numerical simulation experiments, and the results show that the least square algorithm has an advantage of calculation and is easy to implement, while Kalman filtering algorithm calculation amount is large with complex principle. But when the order of the power series is limited, the accuracy of estimation will be higher with the increasing of iterations.

RF power amplifier; power series model; system identification; least square algorithm; Kalman filtering algorithm

TN722.75

A

10.19358/j.issn.1674- 7720.2017.22.020

仝野.射频功率放大器幂级数模型的系统辨识与实现J.微型机与应用，2017,36(22)：74-77.