发动机试验台测力机构柔性梁设计研究

杨中艳，苏浩，刘丹，孙侃，尹世博

(中国航天空气动力技术研究院 第二研究所，北京 100074)

发动机试验台测力机构柔性梁设计研究

杨中艳，苏浩，刘丹，孙侃，尹世博

(中国航天空气动力技术研究院 第二研究所，北京 100074)

柔性梁的刚度性能影响风洞盒式应变天平的精准度，是发动机试验台测力试验数据精确可靠的重要保证，而柔性铰链更是柔性梁设计的关键所在。首先，借助有限元分析方法对四种典型柔性铰链进行计算分析，优选出综合刚性最好的柔性铰链形式；其次，基于选择的柔性铰链形式，研究三个关键结构参数对铰链刚度的影响；最后，设计五种不同厚度的柔性梁进行有限元分析，并加工实物模型进行加载试验验证。结果表明：铰链宽度b=40 mm、半径R=5 mm、最小厚度t=4 mm时双圆弧柔性梁的综合刚度最好，且侧向柔度大，轴向刚度优；有限元计算值和试验值吻合良好，误差小于5%，表明将有限元方法运用于柔性梁的设计优化是可行、可靠的。

发动机试验平台；柔性梁；柔性铰链；应变天平；刚度；有限元分析

0 引 言

六分量天平是发动机试验台测力机构的核心部件，设计为装配式盒式天平结构，由固定框、浮动框、高精度测力传感器和柔性梁组成，并装配为一个整体。试验时试验台发动机模型安装在测力机构，即装配式六分量盒式天平的浮动框上。测力机构布局如图1所示。

柔性梁是用来传递和分解力的，是六分量天平的重要组成部分，其刚度性能直接影响风洞盒式应变天平的精准度，是发动机试验台测力实验数据精确可靠的重要保证。柔性梁两端有双向柔性铰链，柔性铰链更是柔性梁设计的关键所在[1]。

柔性铰链有多种结构形式，包括圆弧型、圆截面万向型和弹簧片式等。柔性铰链可提供角位移，轴向刚度好，并且无间隙、无摩擦和滞后，被广泛应用于风洞天平、机器人、机械手、精密定位系统，但都为中小载荷[2-5]。20世纪60年代中期，美国联合航空公司首先将弹簧片式柔性铰链引入盒式天平[6]，而后NASA兰利研究中心将圆截面细棒性柔性铰链和双圆弧型柔性铰链引入整体式盒式天平[7]；国内，杨中艳等[8]提出了用双圆弧型柔性铰链代替矩形截面柔性铰链的柔性梁，对提高盒式天平整体刚度、降低各分量之间的干扰，尤其对提高阻力元测量的精度作了突出贡献。贺伟等[9]成功地将双圆弧型柔性铰链应用到单模块超燃发动机推力测量天平的柔性梁设计。但对于大载荷六分量发动机试验台测力机构而言，各分量载荷均在2 t以上，国内外类似应用的研究还是空白， 为了确保测力机构的性能，需针对柔性铰链开展深入地研究工作。

本文采用ABAQUS有限元软件对四种典型柔性铰链在边界条件、最小截面面积和总长度都相同的情况下分析其刚度性能，优选一种综合刚性较好的柔性铰链形式即圆弧型柔性铰链，并给出关键结构参数对其刚度性能的影响关系，以期为双圆弧型柔性梁的设计研究提供理论支持。设计并加工五种不同最小厚度的双圆弧柔性梁，进行有限元刚度分析和侧向加载试验验证，以验证有限元计算的可靠性。

1 柔性铰链模型

在发动机试验台测力试验中，试验者最关心的、也是最具有实际意义的分量是轴向力分量，它反映了发动机在试验气流中阻力的大小[9]。因此，本文根据试验台测力机构阻力分量的设计载荷，计算出单支柔性梁在轴向承受的载荷为20 kN。因其在实际使用中侧向载荷未知，现施加侧向载荷300 N进行柔性梁侧向柔度分析(假设给定小干扰侧向力，约为轴向载荷的1.5%)。柔性铰链的材料选用17-4PH，总长度为35 mm，安全系数取4。

选取的四种典型柔性铰链分别为：矩形截面单向直圆型柔性铰链即圆弧型柔性铰链、圆形截面万向型柔性铰链即柔性球铰、同转动中心圆弧切面双向柔性铰链和矩形截面弹簧片式单向柔性铰链。

根据要求的安全系数，通过力学理论计算[10]，初步确定圆弧型柔性铰链的最小厚度t=3 mm，依据t/R的最佳比值确定R≈5 mm，宽度b=40 mm，最小截面积A=b×t=120 mm2。

在边界条件、最小截面面积和总长度相同的情况下，初步确定其他三种柔性铰链结构尺寸如下：①柔性球铰最小截面半径t≈6.2 mm，圆弧半径R=5 mm，圆心角90°；②同转动中心圆弧切面双向柔性铰链最小厚度t=6 mm，圆弧半径R=5 mm，宽度b=20 mm；③矩形弹簧片式单向柔性铰链最小厚度t=6 mm，直梁部分长度l=10 mm，宽度b=20 mm。

2 柔性铰链有限元分析

利用有限元软件ABAQUS[10-13]建立各种柔性铰链的有限元模型，如图2所示。为了保证有限元计算的准确性，均采用高精度的六面体单元进行网格划分。柔性铰链的完全位移约束施加在底面节点，移动副约束施加在上端面的节点上。柔性铰链应力在许用应力范围内是柔性铰链正常工作的保证。

通过有限元计算，得出各柔性铰链在轴向载荷和侧向载荷单独作用下的应力和最大节点位移值，如表1所示。

表1 单独载荷作用下各柔性铰链的应力与最大节点位移计算结果

从表1可以看出：圆弧型柔性铰链在轴向载荷单独作用下，轴向最大Mises应力和最大节点位移最小，表明其轴向刚度最好；在侧向载荷单独作用下，圆弧型柔性铰链的最大节点位移最大，约为0.023 4 mm，比侧向节点位移最小的柔性球铰的最大节点位移大了0.018 mm，约是柔性球铰的4.5倍，表明其侧向柔度最好；其轴向最大Mises应力为164 MPa，侧向最大Mises应力为65.7 MPa，满足第四强度理论条件，符合强度要求。因此，表明在四种柔性铰链中，圆弧型柔性铰链轴向刚度最好，侧向刚度最小，呈“柔性”，抑制非轴向力的干扰能力强，所以优选该铰链形式作为后续研究。

3 圆弧型柔性铰链关键结构参数对刚度的影响

圆弧型柔性铰链关键结构参数包括最小厚度t、圆弧半径R和宽度b。

R、b一定的情况下，设计五种不同尺寸t，进行有限元刚度分析，得到刚度与最小厚度t的关系，如图3所示。

从图3可以看出：圆弧型柔性铰链轴向刚度与最小厚度t呈线性递增关系，随着t的增加，轴向刚度也近似线性增大；侧向柔度与最小厚度t呈曲线递减关系，且减速越来越平缓，随着t的增加，侧向柔度呈近似二次曲线减小。

t、b一定的情况下，设计五种不同尺寸R，进行有限元刚度分析，得到刚度与圆弧半径R的关系，如图4所示。

从图4可以看出：圆弧型柔性铰链的轴向刚度与圆弧半径R呈线性递减关系，随着R的增加，轴向刚度也线性减小；侧向柔度与圆弧半径R呈线性递增关系，随着R的增加，侧向柔度也线性增加。

t、R一定的情况下，设计五种不同尺寸b，进行有限元刚度分析，得到刚度与宽度b的关系，如图5所示。

从图5可以看出：圆弧型柔性铰链的轴向刚度与铰链宽度b呈线性递增关系，随着铰链宽度b的增加，轴向刚度也线性增加；侧向柔度与铰链宽度b呈线性递减关系，但曲线的斜率小，减速较缓，即铰链宽度b值对圆弧型柔性铰链的侧向柔度的影响并不是特别敏感。

综上所述，圆弧型柔性铰链各结构设计参数对其侧向柔度的影响程度依次为：铰链最小厚度t影响最大，其次为圆弧半径R，最后为铰链宽度b。各结构设计参数对其轴向刚度的影响都为线性关系，其中铰链最小厚度t影响最大。因此，采用改变铰链最小厚度t的方法更易满足圆弧型柔性铰链设计要求。

4 柔性梁有限元分析

测力机构柔性梁用来传递沿其轴向的力，对与轴向正交的另外两个方向呈“柔性”，以此抑制其他分量对轴向分量的干扰。因此，设计圆弧型柔性铰链的双圆弧柔性梁，并针对五种不同结构尺寸t=3、4、5、6、7 mm，进行有限元分析，边界条件同柔性铰链。

双圆弧柔性梁的有限元模型如图6所示，节点A表示柔性梁侧向加载试验输出位移的节点。该柔性梁最小厚度t=4 mm时在轴向力20 kN单独作用下的Mises应力和节点位移云图如图7所示。该柔性梁最小厚度t=4 mm时在侧向载荷300 N单独作用下的Mises应力和节点位移云图如图8所示。

通过有限元计算，得出各柔性梁在轴向载荷和侧向载荷单独作用下的应力和最大节点位移值，如表2所示。

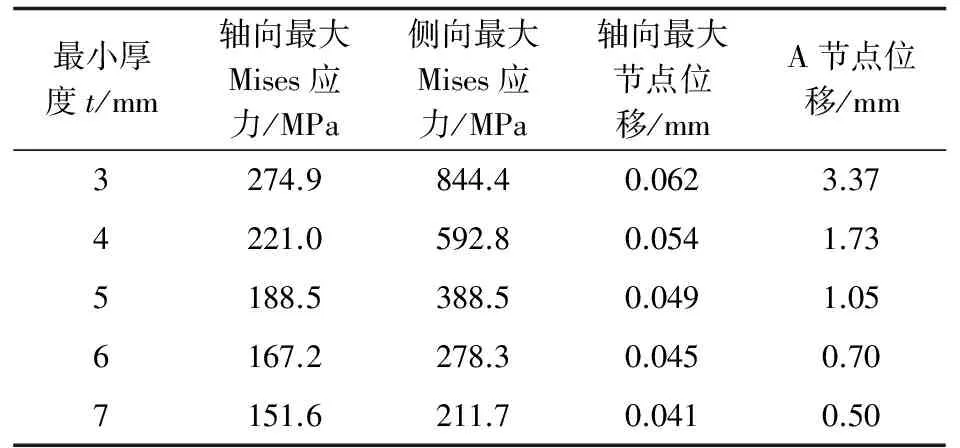
表2 单独载荷作用下双圆弧柔性梁应力与节点位移计算结果

从表2可以看出：随着最小厚度t的增加，双圆弧型柔性梁的轴向最大Mises应力缓慢减小，轴向刚度随之缓慢增加，而其侧向最大Mises应力较迅速地减小，侧向柔度也跟着较迅速地减小；各柔性梁在轴向载荷单独作用下的轴向最大节点位移很小(最大仅为0.062 mm)，其形变变化量最大约为0.021 mm，因此，无法用万能试验机精确地测量其形变变化量，故未做轴向加载试验。

5 试验验证

在专用天平校正架上对柔性梁各试件做侧向加载试验(其示意图如图9所示)，得出双圆弧柔性梁的侧向柔度试验值与有限元计算值的比较结果，如图10所示。

从图10可以看出：双圆弧柔性梁的侧向柔度随着最小厚度t的增加较迅速地减小，并且随着t的增加其计算值与试验值之间的误差也越来越大，虽然柔性梁的侧向柔度计算结果比试验结果偏保守，但其计算与试验结果一致(误差小于5%)，验证了有限元计算的可靠性。表明将有限元方法用于柔性梁的设计，可提高柔性梁的设计效率，降低天平研制成本。

6 结 论

(1) 通过对五种不同结构尺寸t的双圆弧型柔性梁有限元分析及侧向加载试验验证可知，铰链宽度b=40 mm、半径R=5 mm、最小厚度t=4 mm时双圆弧柔性梁的综合刚度最好(其侧向柔度较大，轴向刚度也较优)。

(2) 本文所得到的发动机试验台测力机构阻力分量柔性梁的研究结果，为测力机构其他分量柔性梁的设计研究提供了理论基础和试验依据。

[1] 贺德馨, 等. 风洞天平[M]. 北京: 国防工业出版社, 2001: 97-99.

He Dexin, et al. Wind tunnel balance[M]. Beijing: National Defense Industry Press, 2001: 97-99.(in Chinese)

[2] Paros J M, Weisberg L. How to design flexure hinge[J]. Machine Design, 1965, 137(27): 151-157.(in Chinese)

[3] 李庆祥, 等. 现代精密仪器设计[M]. 北京: 清华大学出版社, 2004.

Li Qingxiang, et al. Design of modern precision instruments[M]. Beijing: Tsinghua University Press, 2004.(in Chinese)

[4] Nicolae lobontiu. Compliant mechanisms: design of the fl-exure hinges[M]. USA: CRC Press LLC, 2003: 447.

[5] 吴鹰飞, 周兆英. 柔性铰链的应用[J]. 中国机械工程, 2002, 13(18): 1615-1618.

Wu Yingfei, Zhou Zhaoying. Application of flexure hinge[J]. China Mechanical engineering, 2002, 13(18): 1615-1618.(in Chinese)

[6] Mole P J. Development of a six-component flexured two-shell internal strain gage balance[EB/OL]. AIAA-93-0793, 1993.

[7] Roberts P W. NASA Langley force and stain measurement capabilities[R]. NASA/CP-1999-209101, 1999.

[8] 杨中艳, 解亚军. 六分量盒式应变天平的有限元分析[J]. 弹箭与制导学报, 2010, 30(2): 201-204.

Yang Zhongyan, Xie Yajun. Finite element analysis of a six-component cassette strain-gauge balance[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2010, 30(2): 201-204.(in Chinese)

[9] 贺伟, 童泽润, 李宏斌. 单模块超燃发动机推力测量天平研制[J]. 航空动力学报, 2010, 25(10): 2285-2289.

He Wei, Tong Zerun, Li Hongbin. Investigation of thrust balance for the single module scramjet[J]. Journal of Aerospace Power, 2010, 25(10): 2285-2289.(in Chinese)

[10] 吴鹰飞, 周兆英. 柔性铰链的设计计算[J]. 工程力学, 2002, 19(6): 136-140.

Wu Yingfei, Zhou Zhaoying. Design of flexure hinges[J]. Engineering Mechanics, 2002, 19(6): 136-140.(in Chinese)

[11] 石亦平, 周玉蓉. ABAQUS有限元分析实例详解[M]. 北京: 机械工业出版社, 2006: 393.

Shi Yiping, Zhou Yurong. Finite element analysis of detailed examples for ABAQUS[M]. Beijing: Machinery Industry Press, 2006: 393.(in Chinese)

[12] 于亚婷, 杜平安, 王振伟. 有限元法的应用现状研究[J]. 机械设计, 2005, 22(3): 6-9.

Yu Yating, Du Ping’an, Wang Zhenwei. Research on the current application status of finite element method[J]. Journal of Machine Design, 2005, 22(3): 6-9.(in Chinese)

[13] 美国ABAQUS Inc. ABAQUS有限元软件6.4版入门指南[M]. 庄茁, 朱以文, 肖金生, 等译. 北京: 清华大学出版社, 2004: 365.

ABAQUS Inc. in USA. The finite element software version 6.4 entry guide for ABAQUS[M]. Translated by Zhuang Zhuo, Zhu Yiwen, Xiao Jinsheng, et al. Beijing: Tsinghua University Press, 2004: 365.(in Chinese)

杨中艳(1983-)，女，硕士，工程师。主要研究方向：天平与模型设计。

苏浩(1987-)，男，工程师。主要研究方向：天平与模型设计。

刘丹(1979-)，男，硕士，高级工程师。主要研究方向：天平与模型设计。

孙侃(1976-)，男，硕士，高级工程师。主要研究方向：天平与模型设计。

尹世博(1973-)，男，硕士，高级工程师。主要研究方向：低速风洞试验技术。

(编辑：赵毓梅)

ResearchonFlexibleBeamofForceMeasuringMechanismofEnginePlatform

Yang Zhongyan, Su Hao, Liu Dan, Sun Kan, Yin Shibo

(The Second Research Institute, China Academy of Aerospace Aerodynamics, Beijing 100074, China)

The flexible beam’s stiffness performance directly affects the accuracy of wind tunnel cassette strain gauge balance, and it is an important guarantee for accuracy of test data of engine test bench, whereas flexible hinge design is the key of flexible beam design. Firstly, four kinds of typical flexible hinges are analyzed by finite element method, and one flexible hinge which has good integrated stiffness is selected. Secondly, for selected hinge style, the influence of three key structural parameters on hinge stiffness performance is researched. Finally, basis on above research, five kinds of min-thickness flexible beams are designed and analyzed by finite element method, and their stiffness performance are validated by loading test. The result shows that the hinge widthb=40 mm, radiusR=50 mm and min-thicknesst=40 mm can get best stiffness performance, in addition, there is a good agreement between calculation and test(the maximum error is less than 5%). It indicates that by using the finite element method, the design and optimization of flexible beam are feasible and reliable.

engine platform; flexible beam; flexible hinge; strain gauge balance; stiffness; finite element analysis

苏浩,13720041809@163.com

1674-8190(2017)04-465-06

V211.72

A

10.16615/j.cnki.1674-8190.2017.04.015