飞行数据相容性检验方法

李富刚，张聪，田福礼，张喆

(中国飞行试验研究院 飞行仿真实验室，西安 710089)

飞行数据相容性检验方法

李富刚，张聪，田福礼，张喆

(中国飞行试验研究院 飞行仿真实验室，西安 710089)

飞行试验测量数据中存在过程噪声和测量噪声，导致飞行数据之间不相容，国内目前常用的输出误差法不适用于耦合严重的直升机飞行数据相容性检验。采用增广卡尔曼滤波方法进行状态估计，大幅度地消除测量值中的误差；再用输出误差法对增广卡尔曼滤波估计的结果进行相容性检验，并将其应用于直升机四阶纵向等效模型辨识中。结果表明：提出的这种方法既解决了单独使用增广卡尔曼滤波进行数据相容性分析时由于初期收敛过程造成的滤波误差问题，又克服了单独使用输入误差法进行数据相容性时需手动修改时间延迟问题和测量值中误差过大时输出误差法无法收敛问题，使得检验效果与计算效率大幅提升。

增广卡尔曼滤波；相容性检验；飞行试验；状态估计

0 引 言

飞行数据相容性检验是通过对测量量的尺度因子误差、系统误差进行适当的修正，使得各个通道所测得的飞行数据彼此相容，即满足飞机运动方程。该项工作引起多数国家的重视[1-2]，并且相继出现了一系列算法，例如：增广卡尔曼滤波算法、最小二乘算法、极大似然法、极大似然法的简化方法输出误差法等[3]。直升机飞行数据相容性检验是直升机模型辨识工作的必备步骤和关键部分，目前，国内的研究主要集中在数据相容性检验后的模型辨识部分，对直升机数据相容性检验的研究较少[4-6]。国内，主要采用极大似然法及输出误差法进行飞行数据相容性检验。极大似然法为局部寻优，其固有缺点是当测量值中的误差过大(远离最优点)时，算法不易收敛甚至发散，而且还需通过对比由角速率积分得到的姿态角和测量姿态角之间的时间差，手动修正时间延迟。卡尔曼滤波初期收敛过程造成滤波误差，致使滤波结果前面部分效果差、后面部分效果好的现象。英国J2航空公司的飞机模型辨识软件中数据相容性检验部分采用卡尔曼滤波方法与其他方法结合的方法[7]。

本文将两种方法相结合，先用增广卡尔曼滤波方法进行整体估计，大幅消除测量数据中的误差，再用输出误差法对估计结果进行相容性检验。集成增广卡尔曼滤波和输出误差法的飞行数据相容性检验技术同时具备两种方法的优点，又可以克服两种方法原有的缺点，以期将该技术应用于飞机模型验证前期的数据相容性检验。

1 建 模

1.1 飞行数据相容性检验模型建立

用于飞行试验数据相容性检验方程如下：

(1)

假设输入量误差模型：

(2)

观测量误差模型：

(3)

式中：λ为缩放因子；ε为稳态差；η为均值为0的测量噪声，带下标e的量表示测量值。

将输入方程组(2)和方程组(3)代入方程组(1)中，将需要估计的缩放因子、稳态误差增加到状态量中，即得到飞机运动的状态方程和观测方程：

(4)

zk=h(xk)+uk

(5)

式中：

x=[u,v,w,φ,θ,ψ,xg,yg,h,λ,ε]T

u=[axe,aye,aze,pe,qe,re]T

w=[ηax,ηay,ηaz,ηp,ηq,ηr]T

zk=[φe,θe,ψe,αe,βe,Ve,xge,yge,he]T

uk=[ηφ,ηθ,ηψ,ηα,ηβ,ηv,ηxg,ηyg,ηh]T

λ=[λax,λay,λaz,λp,λq,λr,λφ,λθ,λψ,λα,λβ,λv,λxg,λyg,λh]

ε=[εax,εay,εaz,εp,εq,εr,εφ,εθ,εψ,εα,εβ,εv,εxg,εyg,εh]

得到方程(4)和方程(5)后，即可利用增广卡尔曼滤波理论对模型中的参数进行高精度估计和数据重构。

1.2 增广卡尔曼滤波理论

假设带误差的非线性系统模型和观测模型如下[8-13]：

(6)

zk=h(xk)+vk,vk～N(0,Rk)

(7)

式中：x,u为系统状态量和输入量；zk为观测量；f、h为状态方程组函数和观测方程组函数；w(t)，vk为过程激励噪声和观测噪声，假设它们是相互独立并满足正态分布的白噪声；N[0,Q(t)]、N(0,Rk)为正态分布，Q(t)、Rk为协方差矩阵；xk=x(tk)。

对状态方程和观测方程的一阶(或者二阶)泰勒展开近似进行卡尔曼滤波，即为增广卡尔曼滤波。本文采用一阶泰勒近似，具体算法过程如下：

第一步：状态量、状态量误差协方差矩阵初始值选择

P0|0=Var[x(t0)]

第二步：状态量、误差协方差矩阵预测

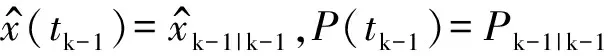
(8)

第三步：增益、状态量、状态量误差协方差矩阵更新

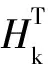
(9)

(10)

Pk|k=(I-KkHk)Pk|k-1

(11)

方程组(8)～方程组(11)即为增广卡尔曼滤波的主要部分。循环第二步和第三步直到数据段结束。

将该理论应用于求解1.1节中推导得到的方程(4)和方程(5)中的状态量、偏差、尺度因子的估计。

1.3增广卡尔曼滤波初值选择，噪声协方差矩阵计算

在进行滤波之前，先要估计状态量x和误差协方差矩阵P的初值。状态量中的u,v,w,φ,θ,ψ,xg,yg,h的初值取试飞数据中试飞动作的开始时前几秒稳态状态的平均值；εax,εay,εaz,εp,εq,εr,εφ,εθ,εψ,εα,εβ,εv,εxg,εyg,εh的初值，由相应的试飞数据的测量值经过低通滤波后再与原测量值相减得到的噪声的平均值；其余状态量的初值选为0。

P值的大小，表示对状态量初始值的信任程度，影响估计过程中的初始阶段估计的效果。观测量和输入量对应P的对角线上的初值，通过响应量的噪声的方差计算。可根据具体估计情况，适当的调节P的初值。

噪声协方差矩阵Q由输入量u=[axe,aye,aze,pe,qe,re]T减去其经过低通滤波的值得到噪声的方差。噪声协方差矩阵R计算过程与Q计算类似。需要说明的是：这里应用的增广卡尔曼滤波实际上是对非线性方程，利用一次泰勒展开来逼近，因此Q、R由噪声的协方差和一阶泰勒展开余项的误差组成。在算法的调试过程中，适当的改变Q、R，来改变对惯导、GPS等测量数据的信任程度。

2 实际应用

2.1 相容性检验

以直升机中速平飞时的纵向脉冲动作为例进行飞行数据相容性检验。为了作比较，首先采用输出误差法直接进行数据相容性检验。首先对数据进行检查，检查结果如图1所示，发现姿态角均有时间延迟，误差较大；再用输出误差法进行相容性检验，检验结果如图2所示。

从图2可以看出：姿态角时间延迟没有消除，需要手动调整角速率测量值和测量时间对应关系后重新检验一次才能消除时间延迟，并且辨识算法没有收敛，没有收敛的原因是过载中的误差较大导致。

利用增广卡尔曼滤波进行数据相容性检验，结果如图3～图4所示，可以看出：姿态角的时间误差已经被去掉，但是由于增广卡尔曼滤波初期的收敛过程导致初期的滤波效果不好。

对增广卡尔曼滤波进行数据相容性检验，结果如图5所示，再利用输出误差法进行相容性检验，结果如图6所示。

从图5～图6可以看出：姿态角时间延迟被消除，同时由增广卡尔曼滤波算法初期收敛造成的误差也被消除；在相同收敛条件判据下，使用本文提出的综合的数据相容性检验技术迭代16次后就收敛，耗时20 s；单独使用输出误差法时，则迭代499次，达到设置的循环上限，未收敛。本文提出的数据相容性检验技术无需将纵向和横向参数分开进行相容性检验，更适合参数耦合严重的数据相容性检验情形。

2.2 相容性检验数据的应用

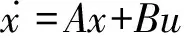
3 结束语

本文提出的相容性检验方法综合了增广卡尔曼滤波和输出误差法的优点，增广卡尔曼滤波估计过程中对状态量和状态量的协方差矩阵进行积分，克服了输出误差法手动修改时间延迟的缺点，并且克服了这两种方法单独使用时的缺点，提高了相容性检验的效率。该方法已经应用于运动参数耦合严重的直升机模型辨识过程中的飞行数据相关性检验和D级直升机模拟器模型校准及某型直升机的定型试飞。

[1] 史忠科. 飞行数据相容性检验的极大似然方法[J]. 航空学报, 1990, 11(8): B354-B360.

Shi Zhongke. A maximum likelihood method for flight test data compatibility check[J]. Acta Aeronautica et Astronautica Sinca, 1990, 11(8): B354-B360.(in Chinese)

[2] 张友民, 王培德, 张洪才. 估计理论在飞行数据相容性检验中的应用[J]. 航空学报, 1992, 13(7): A398-A402.

Zhang Youmin, Wang Peide, Zhang Hongcai. The application of estimation theory in flight data compatibility check[J]. Acta Aeronautica et Astronautica Sinca, 1992, 13(7): A398-A402.(in Chinese)

[3] 吴伟. 直升机飞行动力学模型辨识与机动飞行研究[D]. 南京: 南京航空航天大学, 2010.

Wu Wei. Identification of helicopter flight dynamics model and investigation on maneuver flight[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010.(in Chinese)

[4] 孙涛. 直升机飞行力学模型辨识研究[D]. 南京: 南京航空航天大学, 2010.

Sun Tao. Research on helicopter flight dynamics model identification[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010.(in Chinese)

[5] 王云龙. 直升机气动参数辨识及机动飞行仿真[D]. 哈尔滨: 哈尔滨工业大学, 2007.

Wang Yunlong. Helicopter aerodynamic parameters identification and tactical flight simulation[D]. Harbin: Harbin Institute of Technology, 2007.(in Chinese)

[6] 魏爱玉. 直升机气动参数辨识方法研究[D]. 西安: 西北工业大学, 2013.

Wei Aiyu. Research on identification method of pneumatic parameters of helicopter[D]. Xi’an: Northwestern Polytechnical University, 2013.(in Chinese)

[7] Jesse Jeck, Zhao Min. J2 universal flight matching process workshop[R]. Xi’an: Xi’an Jesse Technology Co., Ltd, 2016: 10-25.

[8] Frank L Lewis, Dan Popa, Lihua Xie. Optimal and robust estimation[M]. USA: CRC Press, 2007: 272-290.

[9] 张晓莹. 非线性卡尔曼滤波的一点讨论[D]. 广州: 中山大学, 2010.

Zhang Xiaoying. A note on nonlinear kalman filter[D].Guangzhou: Sun Yat-sen University, 2010.(in Chinese)

[10] Reif K, Günther S, Yaz E, et al. Stochastic stability of the continuous-time extended kalman filter[J]. IEE Proceedings-Control Theory and Applications, 2000, 147(1): 45-52.

[11] Vladislav Klein, Eugene A Morelli. Aircraft system identification theory and practice[M]. USA: American Institute of Aeronautics and Astronautics, 2005: 190-290.

[12] 刘超, 刘庆, 田福礼. 用于气动导数辨识的试飞数据处理方法研究[J]. 航空工程进展, 2014, 5(2): 188-192.

Liu Chao, Liu Qing, Tian Fuli. Research on flight test data processing method applied to the identification of aerodynamic derivative[J]. Advances in Aeronautical Science and Engineering, 2014, 5(2): 188-192.(in Chinese)

[13] 萧德云. 系统辨识理论及应用[M]. 北京: 清华大学出版社, 2014: 197-215.

Xiao Deyun. Theory of system identification with applications[M]. Beijing: Tsinghua University Press, 2014: 197-215.(in Chinese)

李富刚(1986-)，男，硕士，工程师。主要研究方向：飞机建模与模型验证。

张聪(1986-)，女，硕士，工程师。主要研究方向：飞行仿真与控制。

田福礼(1965-)，男，博士，研究员。主要研究方向：飞行仿真与控制。

张喆(1986-)，男，硕士，高级工程师。主要研究方向：飞行控制。

(编辑：赵毓梅)

MethodforFlightDataCompatibilityAnalysis

Li Fugang, Zhang Cong, Tian Fuli, Zhang Zhe

(Flight Simulation Laboratory, Chinese Flight Test Establishment, Xi’an 710089, China)

Process noises and measure noises exist in flight test data, which lead to incompatibility of flight data. The output error method that is the popular method used in flight test data compatibility checking recently is not fit for helicopter model data compatibility checking with serious coupling. Extended Kalman filter is applied for states estimation and error in the measured value is eliminated drastically. Compatibility analysis for results of extended Kalman filter is carried on by way of output error method. This technology is used in the fourth order liner equivalent model identification of helicopter longitudinal. By this technology, problems of wave filtering errors which are caused by extended Kalman filter primary convergence are solved, and problems of time delay modification by hand in output error method is conquered and non-convergence of output error method when errors in measuring data are big is solved, respectively. Verification effect and computational efficiency are greatly improved.

extended Kalman filter; compatibility analysis; flight test; state estimation

2017-03-05；

2017-06-11

李富刚,18192593036@163.com

1674-8190(2017)04-479-07

V217

A

10.16615/j.cnki.1674-8190.2017.04.017