民用旅客机撤离过程动态引导方法研究

郭艳静, 张玉刚

(1.西北工业大学 软件与微电子学院，西安 710072) (2.西北工业大学 航空学院，西安 710072)

民用旅客机撤离过程动态引导方法研究

郭艳静1, 张玉刚2

(1.西北工业大学 软件与微电子学院，西安 710072) (2.西北工业大学 航空学院，西安 710072)

紧急情况下民用旅客机乘客的撤离疏散过程存在无法充分利用所有可用出口的问题，为了减少旅客机紧急情况下乘员的总撤离时间，基于元胞自动机理论，考虑出口可用性动态变化对撤离过程的影响，提出一种旅客机应急撤离过程动态估算方法，制定五类共计20条撤离规则，建立旅客机应急撤离引导模型。以某149座旅客机为例，使用引导模型进行仿真分析，并与未经引导的撤离过程进行对比。结果表明：引导模型可充分利用所有可用出口，可使总撤离时间减少6%以上，最优性能统计值减少30%以上。

旅客机；应急撤离；总撤离时间；最优性能统计；元胞自动机；撤离引导模型

0 引 言

美国联邦航空局、加拿大运输局、英国民用航空管理局联合研究的统计结果显示非致命性事故占飞机总事故比率呈逐年上升趋势，并且非致命事故中引起机上人员死亡的比率呈下降趋势[1]，统计结果表明飞机发生事故后机上大部分人员均能够成功脱险，但由于未能及时撤离出飞机而导致的死亡仍占有重要的一部分[2]。旅客机发生重大故障时，如果迫降成功，乘务员将根据事先制定好的撤离程序引导乘客进行紧急撤离。当出现突发情况时，需要根据主观判断进行撤离引导，容易导致乘客向错误的方向撤离，或是在客舱中形成严重阻塞的问题[3-4]。

为了获得影响应急撤离过程的主要因素及乘员的撤离行为规律，近年来先后建立了GPSS模型[5]、MA模型[6]、OOO模型[7]、airEXODUS模型[8-9]、DEM模型[10]、VacateAir模型[11-12]、CAEESS模型[13]、EvacuSimulation模型[14]、SOAEE模型[15]、PAXelerate模型[16]、FGCAE模型[17]等用于旅客机的应急撤离仿真研究。R.P.Silva等[18]研究了出口可用性和乘客出口选择对总撤离时间的影响，结果表明在不同的出口可用性情况下，乘客出口选择对总撤离时间影响显著。

在最优路径规划及总撤离时间优化方面，苗志宏等[19]利用光滑粒子流动力学方法(SPH)提出了一种将火灾动力学模拟结果耦合到疏散模型中的方法。傅军栋等[20]基于蚁群算法研究了火灾情况下最佳的疏散路线规划问题。Zhang Q S等[21]考虑了一氧化碳对撤离的影响，建立了A380旅客机有火源情况下应急撤离过程的仿真模型，建议通过乘务员来指挥机上乘客向飞机前后部舱门撤离以达到优化撤离时间的目的。

飞机紧急迫降成功后，乘务员如何及时地通知机上乘客有哪些可用出口，如何合理地分配各出口撤离乘客数量，如何快速地引导乘客到达指定出口位置，如何使总撤离时间最优，是保证机上乘员安全、迅速撤离的前提。如何通过有效的手段确保乘务员迅速完成上述任务，或者在乘务员不能完成这些任务时，正确及时地引导乘客撤离飞机，在应急撤离过程中是至关重要的。

为了实现上述目的，减少乘客撤离时间，本文基于元胞自动机理论，通过考虑出口可用性动态变化对撤离过程的影响，提出一种旅客机应急撤离过程动态估算方法，并建立旅客机应急撤离引导模型。此模型结合摄像设备和声音提示设备，以期应用于实际旅客机的应急撤离过程引导服务。

1 旅客机应急撤离过程动态估算方法

如果不考虑乘务员清舱、撤离和飞行员撤离过程，则最优情况应是机上所有的可用出口最后一名乘客同时撤离完毕。为了能够表征这一结果，可以使用最优性能统计(Optimal Performance Statistics，简称OPS)参数。OPS也可用于表示客舱布置的合理程度，OPS参数是由英国格林威治大学火灾安全工程研究室(Fire Safety Engineering Group，简称FSEG)提出的[8]，OPS计算公式如下：

(1)

式中：n为撤离可用出口数量，n≥2；Texiti为出口i最后一位乘客撤离时间(s)；Ttotal为总撤离时间(s)，即max[Texiti]。

由OPS计算公式可得，为了使OPS值最小，需要所有可用出口同时撤离最后的乘客。为了实现这一目的，需要能够掌握撤离过程中各出口等待乘客情况，能够引导乘客向乘客等待数量较少的出口方向运动。为此，本文提出一种动态估算方法，用来快速估算各出口需要的撤离时间，其中各出口等待撤离乘客情况可通过在客舱天花板上安装摄像监视设备或地板安装距离传感器获得，引导乘客向不同出口方向撤离可通过在客舱不同位置安装声音提示装置实现。

以某149座旅客机客舱(如图1所示)为例，客舱含有3对出口，分别是前部C型出口L1/R1、中部Ⅲ型出口L2/R2、后部C型出口L3/R3。

在推导估算方法前，首先定义如下客舱术语：

①机身站位：飞机上各装置或设备在前后方向的位置，例如L1和R1出口的机身站位相同；

②客舱分区：在某两个机身站位之间的客舱区域，例如客舱从前向后可分成A区、B区、C区三个客舱分区；

③出口等待乘客数量：以某出口为目标出口的、尚未撤离出去的乘客数量；

④决策乘客：目标为当前出口(设为出口1)的乘客中如果某个乘客向其他出口(设为出口2)移动，第一个遇见的乘客的目标出口如果是出口2的话，则此乘客为决策乘客，即决策乘客可以选择其他出口为目标；

⑤路径可通：如果当前出口的决策乘客能够撤离到另一个出口的决策乘客处，则称为这两个出口路径可通；

⑥路径阻塞：如果当前出口的决策乘客不能撤离到另一个出口的决策乘客处，则称为这两个出口路径阻塞。

旅客机客舱撤离过程中某一时刻乘客分布情况如图2所示。虽然决策乘客2后面还有两位乘客，但后面的两位乘客在此时刻没有可选的路径，当他们从座椅区域撤离到通道区域时，将成为决策乘客。决策乘客1对出口L2/R2来说路径可通，对出口L3/R3来说路径阻塞；决策乘客2对出口L1/R1来说路径可通，对出口L3/R3来说路径阻塞；决策乘客3对出口L1/R1来说路径阻塞，对出口L3/R3来说路径可通。

在撤离开始后，声音提示装置用于通报各出口可用状态，摄像监视设备用于反馈客舱乘客撤离情况，当所有可用出口打开后，开始启动实时动态估算方法，方法描述如下：

①将机身站位相同或位置近似的出口设为一对出口，如果这对出口的2个出口均可用，则在估算时将这对出口看作一个出口，并将出口的撤离性能乘以2。各种类型出口性能如表1所示。

表1 不同类型出口对应的最大允许座位数量及撤离性能

②获得各出口等待乘客数量，判断决策乘客；

③针对某一决策乘客，如果其目标出口的等待乘客数量与其他可用出口的等待乘客数量满足式(2)，则此决策乘客将更改目标出口。

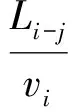
(2)

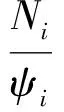
(3)

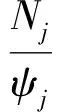
(4)

式中：Ti为决策乘客i对应的目标出口所有等待乘客撤离完毕预估时间(s)；Tj为出口j所有等待乘客撤离完毕预估时间(s)；Li-j为决策乘客i到出口j的路径长度(m)；vi为决策乘客i的移动速度(m/s)；ε为容差阈值(s)；Ni为决策乘客i对应的目标出口等待乘客数量；Nj为出口j等待乘客数量；ψi、ψj为出口的撤离性能，如果为一对可用出口，则乘以2。

2 旅客机应急撤离引导规则

人员撤离过程是个十分复杂的过程，按照场景中不同人员各自意志的行走模式可分为最短距离行为模式、进出一致行为模式和完全从众行为模式，以及混合疏散行为模式[23]。最短距离行为模式假设个体对周围环境非常熟悉，完全了解出口的方向和位置，因而可以采取直接寻找距离自己最近的出口进行疏散的行为；进出一致行为模式用于表现个体对周围环境不太熟悉，只能凭记忆寻找自己进来时的出口，按原路返回的疏散行为；完全从众行为模式则假设个体在惊惶失措的情况下完全丧失了自己的判断能力，只能盲目地追随大多数人进行疏散的行为；混合疏散行为模式则表示人员在撤离过程中表现出了上述多个疏散行为模式。

建模时不可能考虑到所有的因素，在研究条件有限的情况下，对应急撤离过程进行以下假设：

①各类型出口打开时间采用国外典型旅客机应急撤离适航演示验证中的时间分布；

②假设所有乘员通过出口处应急撤离滑梯的时间相同；

③撤离过程行为较为复杂，假设可以通过场景熟悉因子模拟撤离过程乘员表现的行为模式；

④在恐慌状态下，个人情绪变得十分紧张，从而产生一些不理性的竞争行为，本文通过恐慌系数来模拟竞争行为的激烈程度；

⑤模型中不考虑盲从行为，行走模式采用最短距离行为模式；

⑥假设乘客完全服从乘务员的指挥；

⑦中国人群与外国人群具有差异性，但缺少中国人群在飞机紧急情况下的特性数据，模型假设中外人群特性相同，采用国外试验数据，模型中主要使用了反应延迟时间、出口迟疑时间、最大运动速率；

⑧不考虑环境因素(例如照明、烟雾、火灾等)对撤离过程的影响。

为了能够建立模拟撤离过程的各种规则，首先需要在元胞空间的基础上建立各可用出口的地势场，如图3(a)所示，物理场景其元胞空间如图3(b)所示，相应的出口的地势场如图3(c)所示。假设在物理场景中有障碍、可越障碍、出口、人员四种类型对象，转换为元胞空间后，障碍值为1，可越障碍值为2，出口值为3，人员值为10。根据Dijkstra方法计算以出口为目标点的各元胞位置的最短路径，获得地势场图，地势场值考虑了障碍、可越障碍等的影响，此处可越障碍点的地势场值按照2倍无障碍地势场值计算。例如图中四方格子横向和竖向增长值为10个单位，斜向增长值为14个单位，可越障碍处则为20个单位。

(1) 规则1-出口选择规则：①乘务员未指定撤离出口并且出口可用性未知时，按照最近出口方向撤离；②如果有多个距离相等的出口，则使用规则2中的随机方法随机选择；③如果最近出口不可用，则寻找下一个最近出口，直至找到可用出口；④乘务员为乘客指定撤离出口时，按照乘务员指定的出口撤离。

(2) 规则2-人员运动方向规则：①乘员所在元胞的邻域内，如果某个元胞状态为障碍(乘客座椅、乘务员座椅、飞行员座椅、厨房、盥洗室、储藏室、隔板等)，则此元胞位置不可用；②乘员所在元胞的邻域内，所有可用元胞位置采用规则1的选择出口地势场值进行排序，根据场景环境熟悉程度因子按照式(5)计算各元胞概率，所有概率求和归一化后计算各元胞归一化概率，搜索最大概率元胞，如果最大概率值大于等于0.5，认为是方向明显，直接选择此元胞位置作为下一步运动方向；③如果直接选择的元胞位置已被其他乘员占据，则此步等待；④如果最大概率值小于0.5，认为是方向不明显，采用轮盘赌方式随机获得下一步运动方向；⑤如果有多个最大概率值，按照轮盘赌方式随机获得下一步运动方向；⑥如果乘员所选元胞位置已被其他乘员占据，则此步等待。

元胞周围加上本身位置共有9个可能的行走方向，相应的有9个概率值，如图4所示。各个方向选择概率计算公式如下：

pij=Nnij/exp(ksSij)

(5)

(3) 规则3-人员运动速度规则：①乘员运动时按照其能够达到的最大运动速度前进；②可达到的最大运动速度值受到是否存在可越障碍的影响；③可达到的最大运动速度值受到恐慌水平的影响。

人员最大运动速度受到本身性别和年龄的限制，撤离过程中某一时刻实际运动速度还受到所在位置是否有可越障碍、恐慌水平等的影响。如果过道中有可越障碍物(旅客机应急撤离适航审定中要求在过道中散落一些个人随身物品或座椅靠垫、毛毯等)将会对运动速度产生一定的影响。适当的恐慌水平则会提高移动的速度，但过高的恐慌又会带来乘员间的竞争加大，甚至产生拥挤阻塞现象(恐慌产生的竞争由规则4-附加规则部分模拟)。

为了模拟这些因素对撤离速度的影响，采用加权法计算乘员某一时刻的实际运动速度。

vk=max(vkmax,vkmax+kμμ-koo)

(6)

式中：max(.,.)为取两值中最大值；vkmax为乘员k最大运动速度；kμμ为恐慌水平影响因子及乘员k恐慌水平；ko,o为可越障碍影响因子及乘员k处是否有可越障碍指示。

其中乘员最大运动速度vkmax与年龄、性别等人的本身属性相关，本文采用E.R.Galea[8]统计整理的最大运动速度数据范围(如表2所示)随机生成，此数据来源于对现有飞机应急撤离试验录像中人员运动速度数据的统计分析。

表2 乘员最大运动速度范围

(4) 规则4-附加规则：①如果乘员的反应延迟时间未到，则等待进入下一时间步；②乘员位于出口位置时，如果出口迟疑时间未到，则在出口处等待进入下一时间步；③整个元胞空间内如果有多个乘员竞争同一个元胞位置，则按等概率随机竞争成功者，并根据恐慌水平按一定概率产生全部竞争不成功事件。

乘员反应延迟时间和出口迟疑时间典型分布范围根据E.R.Galea[8]统计结果。

客舱中乘务员的位置、数量、指挥能力对撤离过程中乘客的撤离行为、撤离速度均有影响。为了模拟乘务员的影响，需要在模型原有的规则基础上增加新的规则。

(5) 规则5-乘务员规则：①撤离开始时乘务员查看负责的出口可用性情况，并打开可用出口，如果此出口不可用则寻找下一个可用出口；②打开出口后，乘务员开始指挥乘客撤离，乘务员的指挥对乘客的影响具有一定的作用区域，区域大小为以乘务员位置为中心的半径为R的圆形区域；③位于乘务员作用区域内的乘客，其目标出口由乘务员指定，指定方法如图5所示和式(7)决定；④区域内乘客全部撤离后，乘务长开始清舱，其他乘务员直接撤离。

乘务员指挥乘客选择哪一个可用出口是根据区域内当前乘客与可用出口之间其他待撤离乘客数量决定的，假设区域内共有n个可用出口，乘客k与这些可用出口之间的其他待撤离乘客数量分别是m1,m2,…,mn，这些可用出口与乘客k的路径长度分别是L1,L2,…,Ln，则为乘客k指定的撤离出口为

(7)

式中：(Ei,…,Ej)为区域内当前乘客与可用出口之间其他待撤离乘客数量最少的出口列表；E为等待乘客最少的出口中距离当前乘客路径最短的出口。

所有出口的可用性在撤离开始时均是未知的，当出口有乘务员负责时，由乘务员查看出口可用情况，可用时则打开出口，出口不可用时则寻找其他可用出口并指挥乘客转向其他可用出口撤离；当出口没有乘务员撤离时，则由最早到达的乘客负责打开可用的出口。

乘客在撤离过程中也可能会发生当前可用的出口由于通道阻塞或者出口处存在火灾、毒烟、碎片等原因变成不可用状态，乘客需要动态调整自己的目标出口。在某个出口不可用后，计划从此出口撤离的乘客将寻找下一个距离自己最近的出口。

3 引导模型与传统模型撤离仿真对比分析

3.1 某型旅客机客舱布置方案

撤离场景以图1所示单通道旅客机为例，适航演示试验最后一名乘客于64.1 s从R2出口撤离。OPS值为0.02。客舱应急撤离模型如图6所示。

3.2 应急撤离仿真

分别基于CAEESS模型[13]和本文提出的引导模型进行1 000次撤离仿真计算，总撤离时间分布仿真与air EXODUS传统模型计算结果[24]的对比如图7所示，1 000次计算的飞机撤离性能如图8所示。仿真结果表明：air EXODUS传统模型的总应急撤离时间平均值约为70.5 s，使用引导模型之后的总应急撤离时间平均值为66 s，总撤离时间与air EXODUS传统模型相比减少了6%以上；air EXODUS传统模型计算的OPS平均值约为0.10，使用引导模型之后OPS平均值为0.07，OPS值减少了30%以上。

4 结 论

(1) 考虑出口可用性动态变化对撤离过程的影响，提出了旅客机应急撤离过程动态估算方法，基于元胞自动机理论，建立了旅客机应急撤离引导模型。

(2) 在假设成员听从指挥的条件下，撤离过程使用引导方法，能够极大地降低OPS值，从而机上乘员能够更加充分利用所有可用的出口进行撤离。出口利用越充分，所需的总撤离时间就越少，机上乘员成功撤离的几率也就越大。

(3) 在实际旅客机应急撤离过程中，使用引导模型，只有结合人员定位技术和声音提示系统等软硬件，才能使总撤离时间达到较优的目的。机上乘员由于性别、年龄、性格等方面的差异，存在着移动速度、出口处迟疑时间等不同，上述因素直接影响动态估算方法的准确性，因此有必要继续研究如何考虑更多的影响因素，提高估算精度和效率。估算过程只考虑了乘客对所有可用出口利用情况，考虑乘务员的清舱过程，乘务员在最后清舱时，几乎所有可用出口均处于空闲状态，从总撤离时间角度看，本文提出的估算方法还需将乘务员和飞行员加以考虑，从而实现总撤离时间最少的目的。

[1] Cherry R G W amp; Associates Limited. Trends in accidents and fatalities in large transport aircraft. DOT/FAA/AR-10/16[R]. Washington DC: Federal Aviation Administration, 2010: 15-17.

[2] International Civil Aviation Organization. A coordinated, risk-based approach to improving global aviation safety[R]. Canada: International Civil Aviation Organization, 2013: 24-27.

[3] Wang Z Z, Jia F C, Galea E R. Fire and evacuation simulation of the fatal 1985 Manchester airport B737 fire[C]. UK: Downing College, 2012: 159-170.

[4] McLean G A, Corbett C L, Larcher K G, et al. Access-to-egress Ⅰ: interactive effects of factors that control the emergency evacuation of naive passengers through the transport airplane type-Ⅲ overwing exit. DOT/FAA/AM-02/16[R]. Washington DC: Federal Aviation Administration, 2002: 1-35.

[5] Garner J D. GPSS computer simulation of aircraft passenger emergency evacuations. DOT/FAA/AM-78-23[R]. Washington DC: US Department of Transport, Federal Aviation Administration, 1978.

[6] Macey P, Cordey-Hayes M. A computer-based simulation and risk-assessment model for investigation of airliner fire safety[C]. France: Advisory Group Aerospace Research and Development, 1996.

[7] Court M C, Marcus J H. Use of object orientated programming to simulate human behaviour in emergency evacuation of an aircraft’s passenger cabin. DOT/FAA/AM-97/20[R]. Washington DC: US Department of Transport, Federal Aviation Administration, 1997.

[8] Galea E R, Blake S J, Lawrence P J. Report on the testing and systematic evaluation of the airEXODUS aircraft evacuation model. CAA Paper 2004/05[R]. UK: Civil Aviation Authority, 2005.

[9] Galea E R, Blake S J, Gwynne S, et al. The use of evacuation modelling techniques in the design of very large transport aircraft and blended wing body aircraft[J]. The Aeronautical Journal, 2003, 107(1070): 207-218.

[10] Robbins C R, McKee S. Simulating the evacuation of a commercial airliner[J]. The Aeronautical Journal of the Royal Aeronautical Society, 2001, 105(1048): 323-328.

[11] Xue Z, Bloebaum C L. A particle swarm optimization-based aircraft evacuation simulation model-VacateAir[C]. USA: American Institute of Aeronautics amp; Astronautics, 2008.

[12] Xue Z, Bloebaum C L. Human behavior effects on cabin configuration design using VacateAir[C]. Florida: American Institute of Aeronautics and Astronautics, 2009.

[13] Zhang Y G, Xue H J. A new updating strategy in simulating emergency evacuation[C]. Taiwan: Institute of Electrical and Electronics Engineers, 2012, 10: 141-145.

[14] 徐进津. 飞机客舱乘客紧急疏散仿真方法研究[D]. 上海: 上海交通大学, 2011.

Xu Jinjin. The simulation of multiple agents evacuation in an airplane[D]. Shanghai: Shanghai Jiao Tong University, 2011.(in Chinese)

[15] 王炜杰. 大型客机紧急疏散仿真及其标识系统优化研究[D]. 成都: 电子科技大学, 2013.

Wang Weijie. Emergency evacuation simulation for large civil aircraft and evacuation guiding system optimization[D]. Chengdu: University of Electronic Science and Technology of China, 2013.(in Chinese)

[16] Schmidt M, Engelmann M, Brügge-Zobel T, et al. PAXelerate-an open source passenger flow simulation framework for advanced aircraft cabin layouts[C]. AIAA-2016-1284, 2016.

[17] Fang Z M, Lü W, Jiang L X, et al. Modeling and assessment of civil aircraft evacuation based on finer-grid[J]. Physica A, 2016, 448: 102-112.

[18] Silva R P, Ferrari D B, Santos L C C. Uncertainty modeling and assessment in aircraft evacuation simulation[C]. AIAA-2015-714, 2015.

[19] 苗志宏, 李智慧. 火灾环境下人员疏散耦合SPH模型及仿真[J]. 系统仿真学报, 2016, 28(2): 292-300.

Miao Zhihong, Li Zhihui. Coupling SPH model for occupant evacuation in fires and simulation[J]. Journal of System Simulation, 2016, 28(2): 292-300.(in Chinese)

[20] 傅军栋, 刘业辉, 李江辉. 基于蚁群算法的火灾动态疏散[J]. 华东交通大学学报, 2017, 34(3): 118-124.

Fu Jundong, Liu Yehui, Li Jianghui. Fire dynamic evacuation based on ant colony algorithm[J]. Journal of East China Jiaotong University, 2017, 34(3): 118-124.(in Chinese)

[21] Zhang Q S, Qi H P, Zhao G M, et al. Performance simulation of evacuation procedures in post-crash aircraft fires[J]. Journal of Aircraft, 2014, 51(3): 945-955.

[22] Federal Aviation Administration. FAR Part 25. Appendix J airworthiness standards: Transport category airplanes[S]. USA: Federal Aviation Administration, 1999.

[23] 张学锋, 白晨曦. 双层教学楼人员疏散仿真研究[J]. 系统仿真学报, 2017, 29(5): 1070-1076.

Zhang Xuefeng, Bai Chenxi. Study of crowd evacuation in two-story teaching building[J]. 系统仿真学报, 2017, 29(5): 1070-1076.(in Chinese)

[24] Owen M, Galea E R, Lawrence P J, et al. The numerical simulation of aircraft evacuation and its application to aircraft design and certification[J]. Aeronautical Journal, 1998, 102(1016): 301-312.

郭艳静(1980-)，女，硕士，助教。主要研究方向：软件工程、应急撤离仿真与试验。张玉刚(1980-)，男，博士，讲师。主要研究方向：飞行器总体设计、人机工程、应急撤离仿真。

(编辑：赵毓梅)

ResearchonEvacuationDynamicGuidingMethodofPassengerAirplane

Guo Yanjing1, Zhang Yugang2

(1.School of Software and Microelectronics, Northwestern Polytechnical University, Xi’an 710072, China) (2.School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China)

There exist unable to make full use of available exit problems in emergency situations of passenger aircraft. In order to reduce evacuation time of occupant in emergency and improve personnel safety, a dynamic estimating method for aircraft emergency evacuation process is proposed. The method is based on the cellular automata theory. Considering the exits availability impacting on the process of evacuation, an emergency evacuation guidance model is built, in which five kinds of evacuation rules( totally 20 rules) are formulated. For a passenger cabin layout scheme of 149 seats as a case, the overall of aircraft exit are used efficiently with guiding model, the total evacuation time guided by the proposed method is reduced by more than 6% compared with the typical evacuation process, and OPS decreased by 30%.

passenger airplane; emergency evacuation; total evacuation time; optimal performance statistics(OPS); cellular automata; evacuation guiding model

2017-07-07；

2017-09-04

张玉刚,zhangyugang@nwpu.edu.cn

1674-8190(2017)04-457-08

V37

A

10.16615/j.cnki.1674-8190.2017.04.014

收稿日期：2017-06-05；修回日期2017-09-20