瞬态热应力问题的组合杂交有限元方法

张玲，聂玉峰

(西北工业大学 理学院，西安 710129)

瞬态热应力问题的组合杂交有限元方法

张玲，聂玉峰

(西北工业大学 理学院，西安 710129)

求解瞬态热应力问题的杂交元方法面临Ladyshenskaya-Babuska-Brezzi(LBB)条件的检查，其稳定性难以保证，从而提出瞬态热应力问题的组合杂交有限元方法。建立瞬态热应力问题的基于区域分解的组合杂交变分原理及其有限元离散；通过数值算例验证求解瞬态热应力问题的组合杂交元的数值性能。结果表明：在大宽厚比网格下，八节点六面体组合杂交元(CHH(0-1))可以获得与二十节点六面体元(B20)精度相当的位移计算结果和更好的应力计算结果。

瞬态；热应力问题；组合变分原理；稳定性；组合杂交元；大宽厚比；应力精度

0 引 言

在我国的很多国民经济部门，例如电力、航空航天、冶金以及化工等都广泛使用动力机械或者热力发动设备[1-2]，这些设备多数在高温高压的环境下进行作业，设备在启动、停止和运行过程中的温度变化都会引起热应力[3]。特别地，空天飞行器在爬升和返回时，会经受严峻的气动加热，因此空天飞行器热防护系统的材料选取、结构设计和制造方法的研究涉及到力学环境以及热学环境[4]。只有掌握温度变化时所产生的热应力的分布规律，才能保证空天飞行器的安全，因此发展热应力问题的有效求解算法具有重要的意义。

近年来，模拟热力耦合问题有多种方法，例如：有限元方法[5]、无网格方法[6]、多尺度分析方法[7-8]等。与有限元方法相比，无网格方法可以部分或彻底地摆脱网格间的拓扑连接关系，但仅适用于处理大梯度和大变形问题，多尺度分析方法则可以以较少的计算量捕捉到材料的细观尺度行为，但其均匀化方程的求解仍需依靠有限元方法。然而，传统有限元方法存在各种闭锁和对网格畸变敏感等现象，杂交有限元方法不能克服LBB条件这一困难[9]。

基于区域分解的Hellinger-Reissner变分原理及其对偶的变分原理，可以建立一种新的杂交元方法：组合杂交有限元方法[10]。对于弹性力学问题，它具有粗网格高精度、对网格畸变不敏感、不发生locking现象、避免LBB条件检查的特性。从二维到三维，从梁问题到板问题，组合杂交有限元方法在弹性力学问题求解中显示了优越性[11-12]，近年来，它被发展到弹塑性力学问题以及稳态热应力问题的求解方面[13-14]。然而，对于不同的物理问题，组合杂交有限元方法的变分原理不同，有限元离散后，刚度矩阵及右端项不同。

本文首先用传统有限元方法求解瞬态热传导问题，得到初应变之后，发展热应力问题的组合杂交有限元方法，以提高数值求解的精度及效率。

1 瞬态热传导问题求解

三维瞬态热传导问题如下：

(1)

式(1)的等效积分弱形式为

(2)

对上式进行分部积分后，可得

(3)

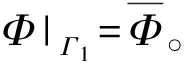
(4)

对于单元内部的温度，采用单元节点的温度通过三线性插值获得，即

(5)

则

(6)

式中：Ni(i=1,2,…,8)为三线性插值基函数；Φi(i=1,2,…,8)为单元节点温度值。

将式(5)和(6)代入式(4)，由于δΦi的任意性，消去该项后，在求解域Ω上，得到瞬态热传导问题的有限元方程。

(7)

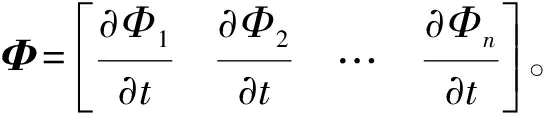
2 热应力问题求解

当物体温度发生变化时，物体由于热变形会产生线应变，如果各部分的热变形不受约束，将不会产生应力。但如果受到的约束或者各部分温度变化不均，即物体热变形不能自由进行，则产生应力，把这部分应力称为热应力。物体由于热膨胀只产生线应变，而剪切应变为0，这种由于热变形产生的应变可以看作物体的初应变[15]。

步骤1 建立热应力问题的组合杂交变分原理

由于存在初应变，与弹性力学问题相比，应力应变关系发生改变，热应力问题的模型为

(8)

(9)

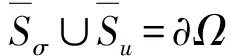
ε0=β(Φ-Φ0)[1 1 1 0 0 0]T

(10)

式中：β为线膨胀系数；Φ0为初始温度。

(11)

(12)

然后，建立热应力问题的组合杂交变分原理。

为了放松场函数的连续性，引入分片定义的Sobolev空间。

通过拉格朗日乘子法建立基于区域分解的变分原理。

(13)

(14)

令

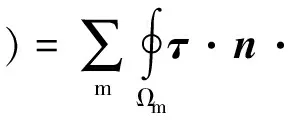
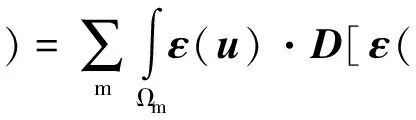
对式(13)～式(14)求变分，得

(15)

(16)

根据v和τ的任意性，式(15)和式(16)的等价表达形式分别为

求(σ,u,uc)∈Γ×U×Uc，使得

(17)

求(σ,u,uc)∈Γ×U×Uc，使得

(18)

根据文献[16]，直接离散鞍点问题(17)或问题(18)均需要满足LBB条件，为了避免LBB条件的检查，引入权系数α∈(0,1)，建立组合杂交变分原理。

求(σ,u,uc)∈Γ×U×Uc，使得

(19)

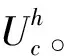
求(uh,σh)∈Uh×Γh，使得

(21)

同理，问题(20)～问题(21)解的适定性可以通过文献[17]得到证明，并根据弹性力学问题误差估计的证明思路，建立如下误差估计：

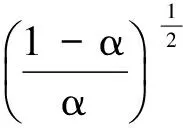
(22)

步骤2 建立高性能组合杂交元

选取线性插值空间为应力插值函数空间，Wilson bubble增强的三线性插值空间作为位移插值函数空间。

(23)

(24)

(25)

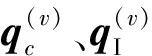
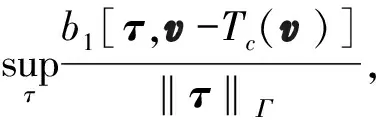
令b1[τ,v-Tc(v)]=0，简化的变分方程如下：

求(uh,σh)∈Uh×Γh，使得

(26)

同时，简化的误差估计为

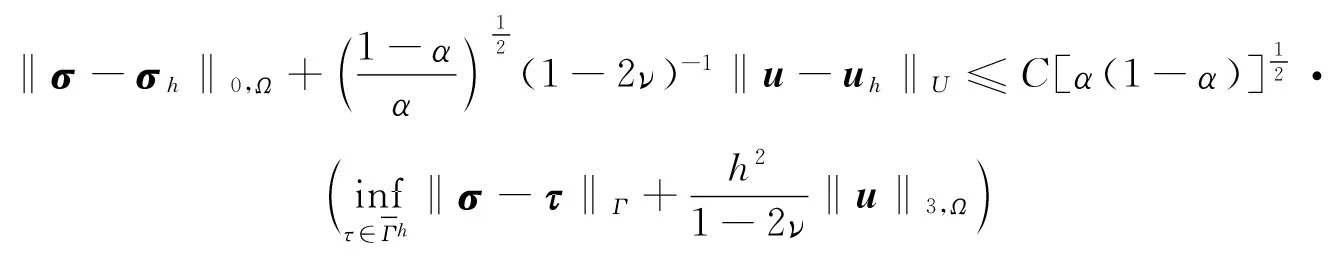
(27)

此时，误差估计阶数提高为O(ht):1lt;tlt;2，并且当h趋于0，得到locking-free收敛性

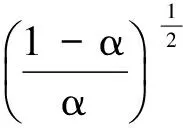
(28)

令b1[τ,v-Tc(v)]=0，则长方体剖分情况下，应力的显式离散表达式见文献[17]。

3 数值实验

通过数值算例来验证求解热应力问题的组合杂交元的数值性能。实验中采用的单元为：组合杂交元(CHH(0-1))、三线性元(H8)、Wilson元(B8)和二次元(B20)，三线性元、Wilson元和二次元的计算结果来自软件Ansys。

算例1 对称板

对称载荷板(由于板的对称性，取其八分之一进行计算)如图1所示，其长、宽、高分别是120、80、4 m。密度为2.5×10-3kg/m3，比热为1.146 J/(kg·℃)，上下表面的对流换热系数为1.8×10-4W/(m2·℃)，4个侧面边界为9.0×10-5W/(m2·℃)。板的弹性模量为7.9×103Pa，泊松比为0.17，热传导率kx=ky=kz=2.46×10-3W/(m·℃)，线膨胀系数β=5.04×10-7/℃，α=0.5。现将板加热到600 ℃并突然放置到20 ℃的空气中进行淬冷，忽略热传导和热辐射，将传热过程简化为对流传热，求板淬冷过程中的热应力变化情况。

当t=100 s时，分析大宽厚比网格下单元H8、B8、B20和CHH(0-1)的位移和应力的计算精度。

B8单元在不同网格剖分下点A(60,0,0)的位移计算结果UX如表1所示，可以看出：点A位移的收敛值为0.597×10-2。

表1 点A(60,0,0)的位移UX

单元H8、B8、B20和CHH(0-1)在大宽厚比网格下点A(60,0,0)的位移计算结果UX如表2所示，可以看出：四种单元均具有较高的位移计算精度。

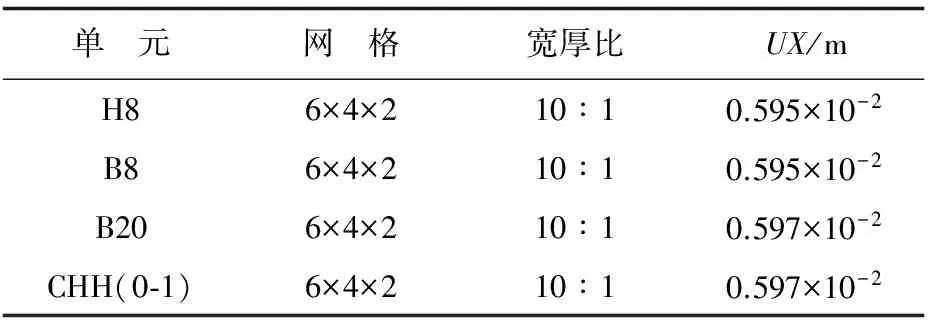
表2 大宽厚比网格下点A(60,0,0)的位移UX

B8单元在不同网格剖分下点F(0,40,2)的应力计算结果σx如表3所示，可以看出：点F应力σx的收敛值为1.307 3。

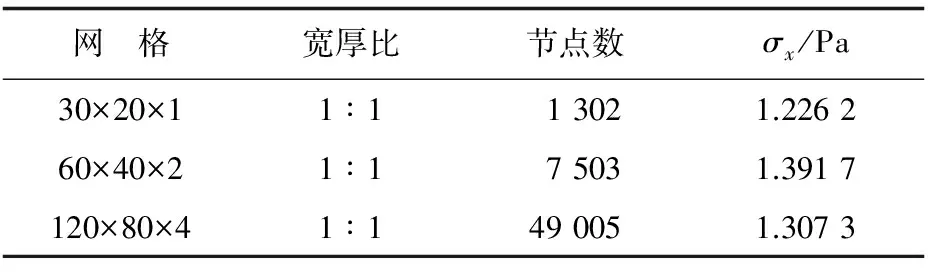
表3 点F(0,40,2)的应力σx

单元H8、B8、B20和CHH(0-1)在大宽厚比网格下点F(0,40,2)的应力计算结果σx如表4所示，可以看出：在10∶1大宽厚比网格剖分下，单元B20和CHH(0-1)的应力精度高于单元H8和B8的应力精度，但单元B20刚度矩阵的计算量是单元CHH(0-1)的5倍，线性方程组阶数是单元CHH(0-1)的4倍[14]。

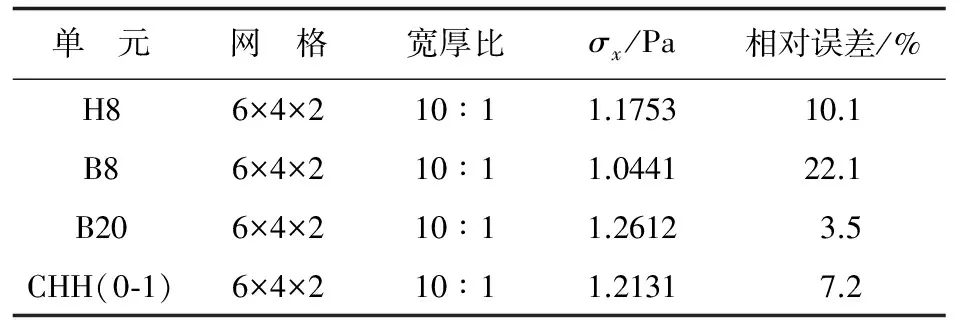
表4 大宽厚比网格下点F(0,40,2)的应力σx

算例2 非对称板

非对称载荷板如图2所示[14]，长、宽、高分别是6、1、0.1 m。密度为2.5×10-3，比热为1.146 J/(kg·℃)，上下表面的对流换热系数为1.8×10-4W/(m2·℃)，4个侧面边界为9.0×10-5W/(m2·℃)。板的弹性模量为1.0×107Pa，泊松比为0.3，热传导率kx=ky=kz=2.46×10-3W/(m·℃)，线膨胀系数β=5.04×10-1℃，α=0.5。板右端给定剪切载荷P=50 N。现将板加热到600 ℃并突然放置到20 ℃的空气中进行淬冷，忽略热传导和热辐射，将传热过程简化为对流传热，求板淬冷过程中的热应力变化情况。

当t=100 s时，分析大宽厚比网格下单元H8、B8、B20和CHH(0-1)的位移和应力的计算精度。

B8单元在不同网格剖分下点B(6,0,0.1)的位移计算结果UZ如表5所示，可以看出：点B位移UZ的收敛值为1.036 6。

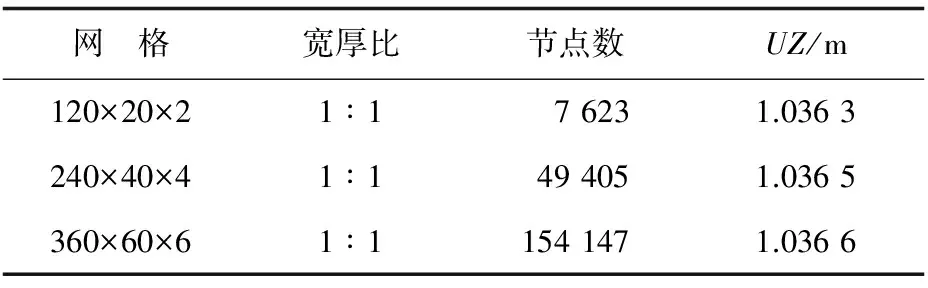
表5 点B(6,0,0.1)的位移UZ

单元H8、B8、B20和CHH(0-1)在大宽厚比网格下点B(6,0,0.1)的位移计算结果UZ如表6所示，可以看出：单元B8、B20和CHH(0-1)在大宽厚比网格下均具有较高的位移计算精度，但单元H8位移精度较差。

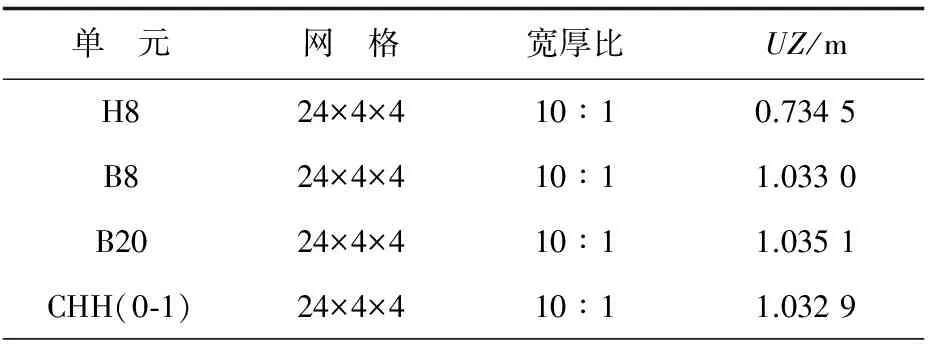
表6 大宽厚比网格下点B(6,0,0.1)的位移UZ

B8单元在不同网格剖分下点A(0.25,0,0)的应力计算结果σx如表7所示，可以看出：点A应力σx的收敛值为0.308 6×108。

表7 点A(0.25,0,0)的应力σx

单元H8、B8、B20和CHH(0-1)在大宽厚比网格下点A(0.25,0,0)的应力计算结果σx如表8所示，可以看出：在10∶1大宽厚比网格剖分下，单元CHH(0-1)应力计算精度高于单元H8、B8、B20的应力计算精度。

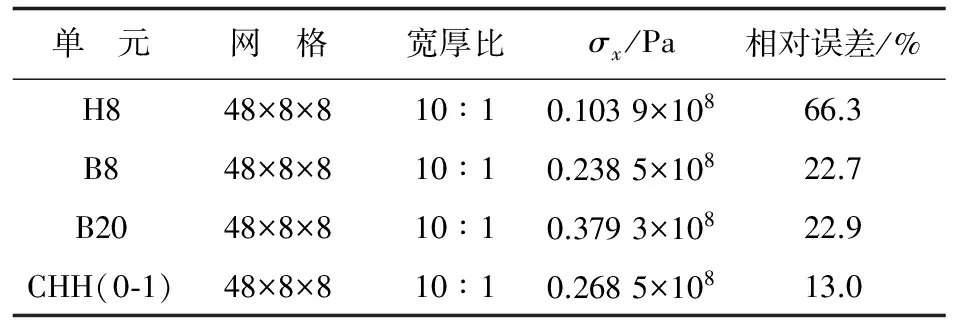
表8 大宽厚比网格下点A(0.25,0,0)的应力σx

综上所述，对于瞬态热应力问题，组合杂交元在大宽厚比网格下可以获得较高的位移和应力计算精度。

4 结 论

本文首先建立瞬态热应力问题的组合杂交变分原理，进而给出其组合杂交有限元方法。组合杂交有限元方法自动满足LBB条件，是稳定的有限元方法。

对于瞬态热应力问题，高性能八节点六面体组合杂交元在大宽厚比网格下可以获得较高的位移和应力计算精度。与传统的有限元方法相比，组合杂交有限元方法可以极大地节约计算量。

[1] Liu W, Qin Y P. Multi-physics coupling model of coal spontaneous combustion in longwall gob area based on moving coordinates[J]. Fuel, 2017, 188: 553-566.

[2] Su H, Rahmani R, Rahnejat H. Thermohydrodynamics of bidirectional groove dry gas seals with slip flow[J]. International Journal of Thermal Sciences, 2016, 110: 270-284.

[3] 崔健. 热应力分析中的应力杂交有限元方法研究[D]. 北京: 华北电力大学, 2002.

Cui Jian. The thermal stress by hybrid finite element method[D]. Beijing: North China Electric Power University, 2002.(in Chinese)

[4] 关春龙, 李壵, 赫晓东. 可重复使用热防护系统防热结构及材料的研究现状[J]. 宇航材料工艺, 2003, 33(6): 7-11, 42.

Guan Chunlong, Li Yao, He Xiaodong. Research status of structures and materials for reusable TPS[J]. Areospace Materials amp; Technology, 2003, 33(6): 7-11, 42.(in Chinese)

[5] Faruk S, Metin S. Elasto-plastic thermal stress analysis in a thermoplastic composite disc under uniform temperature using FEM[J]. Computers amp; Mathematics with Applications, 2006, 11(1): 31-39.

[6] Ren B, Qian J, Zeng X, et al. Recent developments on thermo-mechanical simulations of ductile failure by meshfree method[J]. Computer Modeling in Engineering amp; Sciences, 2011, 71(3): 253-277.

[7] Yang Z Q, Cui J Z, Sun Y, et al. Multiscale analysis method for thermo-mechanical performance of periodic porous materials with interior surface radiation[J]. International Journal for Numerical Methods in Engineering, 2016, 105(5): 323-350.

[8] Yang Z Q, Cui J Z, Zhou S. Thermo-mechanical analysis of periodic porous materials with microscale heat transfer by multiscale asymptotic expansion method[J]. International Journal of Heat and Mass Transfer, 2016, 92: 904-919.

[9] Brezzi F, Fortin M. Mixed and hybrid finite element method[M]. German: Springer-Verlag, 1991.

[10] Zhou T X. Stabilized hybrid finite element methods based on the combination of saddle point principles of elasticity problems[J]. Mathematics of Computation, 2003, 72(244): 1655-1673.

[11] Zhou T X, Xie X P. Zero energy-error mechanism of the combined hybrid method and improvement of Allman’s membrane element with drilling d.o.f.’s[J]. Communications in Numerical Methods in Engineering, 2004, 20(3): 241-250.

[12] Xie X P, Hu J C. Energy-adjustable mechanism of the combined hybrid finite element method and improvement of Zienkiewicz’s plate-element[J]. Communications in Numerical Methods in Engineering, 2005, 21(10): 531-544.

[13] 周天孝. 弹塑性力学的典则变分原理[J]. 数值计算与计算机应用, 2011, 32(1): 1-7.

Zhou Tianxiao. Canonical variational principles in elasticity and plasticity[J]. Journal on Numerical Methods and Computer Applications, 2011, 32(1): 1-7.(in Chinese)

[14] Zhang L, Nie Y F, Yuan Z B, et al. Combined hybrid finite element method applied in elastic thermal stress problem[J]. International Journal of Computational Methods, 2017, 14(3): 1750071.

[15] 王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2008.

Wang Xucheng. Finite element method[M]. Beijing: Tsinghua University Press, 2008.(in Chinese)

[16] Brezzi F, Fortin M. Mixed and hybrid finite element method[M]. German: Springer-Verlag, 1991.

[17] 聂玉峰. 高性能组合杂交有限元方法[D]. 西安: 中国航空计算技术研究所, 2000.

Nie Yufeng. Combined hybrid approach to finite element schemes of high performance[D]. Xi’an: Aeronaut Computing Technical Research Institute, 2000. (in Chinese)

张玲(1987-)，女，博士研究生。主要研究方向：热力学问题的高效有限元方法。聂玉峰(1968-)，男，博士，教授。主要研究方向：科学工程计算的模型、理论与方法。

(编辑：赵毓梅)

CombinedHybridFiniteElementMethodAppliedinTransientThermalStressProblem

Zhang Ling, Nie Yufeng

(School of Natural and Applied Sciences, Northwestern Polytechnical University, Xi’an 710129, China)

The stability of hybrid finite element method of transient thermal stress problem is hard to be guaranteed because of the difficulty of satisfying the ladyshenskaya-babuska-brezzi(LBB) conditions, accordingly, the combined hybrid finite element method of transient thermal stress problem is proposed. Combinative variation principle and the corresponding finite element discretization of transient thermal stress problem is constructed on the basis of domain decomposition technique. The numerical performance of combined hybrid element for solving transient thermal stress problem is verified by numerical experiments. The numerical results indicate that combined hybrid element with 8 nodes(CHH(0-1)) can give almost the same computing accuracy of displacement and better computing accuracy of stress compared with cuboid element with 20 nodes(B20).

transient; thermal stress problem; combinative variation principle; stability; combined hybrid element; big width-to-thickness ratio; stress accuracy

2017-09-26；

2017-10-12

国家自然科学基金(11471262，11501450)西北工业大学博士论文创新基金(CX201524)

聂玉峰,yfnie@nwpu.edu.cn

1674-8190(2017)04-367-08

O242.21

A

10.16615/j.cnki.1674-8190.2017.04.001