Ar-D2O体系束缚态能级的理论计算

王申浩，凤尔银，陶宗明，单会会，麻晓敏

（1.陆军炮兵防空兵学院 基础部，安徽 合肥 230031；2.安徽师范大学 物理与电子信息学院，安徽 芜湖 241000）

Ar-D2O体系束缚态能级的理论计算

王申浩1，凤尔银2，陶宗明1，单会会1，麻晓敏1

（1.陆军炮兵防空兵学院 基础部，安徽 合肥 230031；2.安徽师范大学 物理与电子信息学院，安徽 芜湖 241000）

将D2O分子固定在平衡构型下，得到了Ar-D2O体系的三维势能面.在计算方法上，采用单双迭代（包括非迭代三重激发）耦合簇[CCSD（T）]理论，使用了扩展的相关一致基组aug-ccpVTZ，并且加入了（3s3p2d2f1g）中心键函数.结果显示体系有一个全局最小值，在R=6.91a0，θ=71.25°，φ=0°处，对应的势阱深度是138.7 cm-1，此时Ar-D2O体系是一个平面结构.除了一个全局最小值，体系还有两个一阶鞍点和一个二阶鞍点.为了便于计算体系的束缚态能级，将势能展开成球谐函数的形式，采用3次样条插值的方法得到了径向展开系数vlm(R).通过求解薛定谔方程，得到体系的束缚态能级（J≤2），并在理论上预测了Ar-D2O体系的微波谱及振转贯穿（VRT）谱，理论计算与实验吻合得很好.

Ar-D2O体系；三维势能面；微波谱；振转贯穿谱

0 引言

稀有气体（Rg）原子和H2O分子组成的范德瓦尔斯（vdW）体系受到了人们持续的关注[1-8].究其原因是因为这种体系的相互作用势可以作为研究“憎水”和氢键之间相互作用的模型[9-11].

vdW体系的光谱可以提供体系的几何构型和分子动力学等许多有用的信息，因此在实验上研究vdW体系的光谱就显得尤为重要.稀有气体和H2O分子组成的vdW体系中，Ar-H2O及其H的同位素D组成的体系 Ar-HDO 和 Ar-D2O 的微波谱[12，13]、红外谱[7，14-16]和远红外谱[10，17-19]已有广泛的报道. 实验结果显示 Ar-H2O体系呈平面结构，H2O在Ar-H2O体系中近似是一个自由转子.Jäger及其合作者报道了Kr-H2O[9，20]和Xe-H2O[6]及其各种不同同位素体系的微波谱，Kr-H2O体系的部分微波谱被指认，并给出了体系的结构系数.所有的实验研究结果显示Rg-H2O体系的平衡结构有一个共同特征——所有的原子处在同一个平面上.

理论方面，对于Rg-H2O体系也有广泛的研究.Patkowski[21]和Hodges[22]先后用SAPT和SAPT1的理论方法研究了He-H2O体系的势能面.Hodges[4]用多体微扰理论构建了He-H2O体系的相互作用势.Cohen等[23-24]通过实验数据先后构建了Ar-H2O体系AW1和AW2两个势能面，势能面显示出较强的角向-径向耦合.通过拟合37组光谱数据得到的AW2势能面有一个全局最小值（142.98 cm-1），此时Ar原子位于H2O所在的平面.在ab initio计算方面，Chalasinski等[25]利用多体微扰理论和大基组计算了Ar-H2O的相互作用势.计算得到的势能的最小值（108 cm-1）要远小于AW1势能面的最小值（-174.7 cm-1），和AW2势能面所得到的也有10%的差别.Bulski等[11]利用ab initio计算得到Ar-H2O的相互作用势能的最小值为-157 cm-1.Cohen等构建的势能面最小值的取向在θ=90°与θ=55°之间，这与Chalisinski和Bulski得到的反氢键构型Ar-OH（θ=125°）相反.最近Makarewicz[5]利用单双迭代（包括非迭代三重激发）耦合簇[CCSD（T）]方法和一个大基组来计算Rg-H2O（Rg=He，Ne，Ar，Kr和Xe）的相互作用势.通过比较，Makarewicz计算得到的势能面与Cohen拟合实验数据得到的Ar-H2O势能面具有相似性.

在实验及理论方面，Ar-H2O同位素体系Ar-D2O也有广泛的研究，但在理论上Ar-D2O体系的微波谱和VRT谱却没有被详细地研究.为了得到详细的Ar-D2O体系的光谱数据，为将来的实验数据提供理论依据，本研究采用CCSD（T）的方法计算得到体系的三维势能面，进一步利用构建的势能面计算得到Ar-D2O体系的束缚态能级，并在理论上预测了Ar-D2O体系的微波谱、VRT谱，并与实验光谱做了对比.

1 势能面的计算

1.1 ab initio计算

在计算过程中，将D2O单体看作一个刚性转子，D-O键长和DOD键角固定在平衡结构下.Ar-D2O的分子构型可以用R，θ，φ 3个雅克比坐标表示.如图1所示，R表示Ar原子到D2O单体质心之间的距离，θ表示Ar原子与D2O分子C2轴之间的夹角，当 θ=0°时，Ar原子位于C2轴上.φ描述的是Ar原子相对于Ar-D2O体系构成的平面转动角，当 φ=0°时，Ar原子与D2O单体在一个平面内.

图1 Ar-D2O体系的雅克比坐标表示

对Ar-D2O体系采用CCSD（T）[26]理论计算分子间相互作用势.计算中采用Woon等[27]提出的扩张相关一致基组：aug-cc-pVTZ，同时引入 3s3p2d1f中心键函数（3s和 3p：α＝0.9，0.3，0.1；2d：α＝0.6，0.2；1f：α＝0.3），其中键函数位于Ar原子和D2O分子质心的连线中点，其目的是消除对高角动量函数的要求.在计算体系势能时采用超分子近似[28]的方法来计算每个格点的势能值，并采用Boys等[29]提出的FCP（Full Couterpoise）方法消除基组重叠误差（BSSE）.在做ab initio计算的过程中，格点作如下选取，R取{5.6，5.8，6，6.2，6.4，6.6，6.8，7，7.2，7.5，7.8，8，8.5，9，9.5，10，10.5，11，11.5，12，13，14，15，16，18，20}，θ取 {0°，30°，60°，90°，120°，150°，180°}，φ 取 {0°，15°，30°，45°，60°，75°，90°}，90°-180°之间的相互作用势可由 D2O 单体分子的C2v对称性得到.此次构建势能面共利用了1 274个格点，计算使用MOLPRO 2006[30]程序包.

1.2 势能面的构建

为了便于束缚态能级的计算，将势能V（R，θ，φ）用球谐函数来展开[24]：

式中slm（θ，φ）是归一化的调和球谐函数，考虑到D2O分子是C2v对称性的，所以m只能取偶数，即m=0，2，4，….利用26组Ri所对应的势能值，可以得到下面的矩阵方程：

对矩阵求逆，即可算出一组vlm（Ri），利用同样的方法可以计算出另外25组.对于26组vlm（Ri）利用3次样条插值[31]的方法就可以算出对于给定的（l，m）组合下任意径向R的系数值vlm（Ri），对于角向部分可以通过slm（θ，φ）函数直接计算出.经过仔细的测试，发现nθ×nφ=49个格点足够精确得到展开系数vlm（R），此时对应的组合（l，m）=（6，6），共 16 组.

1.3 束缚态能级的计算方法

Ar-D2O体系在雅克比坐标下的哈密顿量可以写成下面的形式[24]：

式中μ是Ar-D2O体系的约化质量分别是Ar-D2O体系的总角动量算符和D2O单体的角动量算符，表示D2O单体分子包括4次离心畸变常数在内的标准Watson A-约化哈密顿量，其形式[24]为：

式中A，B，C和Δj，Δk，Δjk，δj，δk分别表示D2O分子转动常数和4次离心畸变常数.考虑D2O分子振动基态的情况，其相关常数可以从实验中找到[32].

体系的波函数可按如下基组展开：

式中χq(R)是径向伸展基函数是角向部分基函数，在这里选择如下形式[24]：

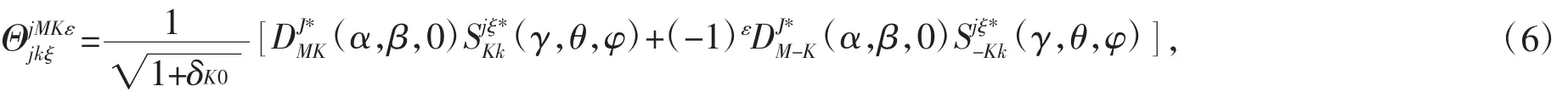
当 J=0，ε=0 时：

对于径向波函数，在这里通过求解下面的一维薛定谔方程得到：

式中v00(R)表示势能展开后的各向同性部分.这种选择有2个优点：第一能方便解释波函数，第二能减小q的数目.利用分立位置表象（DVR）方法可以计算方程的本征值和相应的波函数.利用选定的基组可以计算得到体系的哈密顿量矩阵，通过求解久期方程就可以得到体系的束缚态能级和展开系数.

2 结果和讨论

2.1 势能面特征分析

Ar-D2O体系的势能面有一个全局最小值，位于R=6.91a0，θ=71.25°，φ=0°处，对应的势能为-138.7 cm-1（A点）.此时，Ar-D2O 体系是一个平面结构，Ar原子在垂直 C2轴（θ=90.0°）与氢键构型（θ=55.0°）之间，这与Cohen等构造的AW2[24]势能面结构相吻合.图2（a）是将φ固定在0°时Ar-D2O体系的势能面，从图中可以看出势能很强的角向-径向耦合作用.除了全局最小值，体系还有2个一阶鞍点（B点和C点），对应的是D2O分子在面内的转动.B点位于R=6.83a0，θ=0.0°，C点位于R=6.87a0，θ=180.0°，此时对应的势垒高度分别是 20.2 cm-1和 27.3 cm-1. 除此之外，体系还有一个二阶鞍点（D 点），位于 R=6.83a0，θ=90.0°，φ=90.0°，势垒的高度为56.3 cm-1，此时对应的是D2O分子在面外的转动.图2（b）是将R固定在其平衡结构下θ和φ的二维势能面.因为体系是对称的，所以φ的取向只考虑了0°-180°之间的值，从图中可以看出角向部分有很大的各向异性.

图2 Ar-D2O的二维势能面.（a）φ固定在0°；（b）R固定在6.91a0

2.2 束缚态能级计算

根据 Hutson 等[24]提出的标记方式，Ar-D2O 体系的束缚态可以标记为（nKjkakb，e/f）. 量子数 n=0，1，2，…指的是分子间的伸展振动模（n=0忽略），K是总角动量J在分子坐标轴z轴的投影量子数，K=0，1，2，…用大写的希腊字母Σ，Π，Δ，…标记，描述的是单体分子D2O的转动态.当宇称是p=（-1）J或p=（-1）J-1时分别标记为e对称或f对称.对于C2v对称分子群，一共有4个不可约表示.体系的哈密顿量不会与不同的微扰-反演对称的基函数耦合，因此束缚态波函数可以用C2v的不可约表示来区分[24]：

这样Ar-D2O体系的振转能级可以被划为4个对称的部分A1（even，even），A2（even，odd），B1（odd，even）和B2（odd，odd）.通过这种方法就可以逐一计算各个部分的能级.

表1给出了J为0-2时的几个较低的束缚态能级，并作了标记.从表1中可以看出Ar-D2O体系在基态Σ000的能级为-94.994 cm-1，这意味着零点能为43.7 cm-1.零点能高于势垒的值，这意味着基态的波函数能够畅通无阻地通过势垒.第1激发态Σ101对应D2O单体的转动激发态，束缚态能级是-89.181 cm-1.第一激发态的能级比基态高5.813 cm-1，这与实验值5.880[14]非常接近，比D2O单体低6.304 cm-1，两者之间的区别反映了在Ar-D2O体系中Ar原子对D2O单体的微扰作用.1Σ000比基态高35.362 cm-1，对应的是Ar-D2O体系的第一伸展振动激发态.

2.3 光谱计算

Suzuki等[18]得到了 j=0 以及 j=1 时 Σ111←Σ000和 Π111←Σ000的 VRT 谱，Zwart等[33]观察到了 Π101←Σ101和Π101←Σ101的VRT谱，同时观察到了微波谱.Cohen等[24]通过拟合也到了相关的光谱值.通过已标定的束缚态能级，可以计算得到Ar-D2O体系的微波谱和VRT谱，并与实验测量结果进行了比较.表2给出了3组低能级之间的转动谱，表3给出了J=1←0，j为0-2时10组VRT谱.通过比较发现，对于Ar-D2O体系的微波谱有8组实验数据与理论计算差别较大，这一方面是由于实验或者拟合时能级的标记出现问题；一方面可能是因为微波谱数据较小，导致计算与实验偏差相对较大.Ar-D2O体系的VRT谱实验与理论计算吻合得很好，最大的相对误差只有3%左右.

表1 计算得到的Ar-D2O体系的振转能级

表2 计算得到的Ar-D2O体系的微波谱

表3 计算得到的Ar-D2O体系J=1←0，j为0-2时的VRT谱

3 总结

在CCSD（T）的理论基础上，采用aug-cc-pVTZ基组，同时引入了（3s3p2d1f）键函数.在理论上，构造了完整的Ar-D2O体系的三维势能面，结果显示Ar原子在D2O分子平面比不在平面要稳定.利用自编Fortran程序计算得到了体系的束缚态能级，并与实验得到的微波谱和VRT谱做了对比，计算结果与实验吻合得很好，这也反映出所构造的势能面是可靠的.构造势能面的方法对于研究与Ar-D2O体系相类似的体系是有帮助的.

[1]BARRETO P R P,PALAZZETTI F,GROSSI G,et al.Range and Strength of Intermolecular Forces for Van Der Waals Complexes of the Type H2Xn-Rgwith X=O,Sand n=1,2[J].Journalof Quantum Chemistry,2010,110(3):777-786.

[2]LI S,ZHENG R,ZHU Y,et al.Infrared Diode Laser Spectroscopy of the Ne-D2O Van Der Waals Complex:Strong Coriolis and Angular-Radial Coupling[J].Journalof Chemistry Physics,2011,135(13):134304-134315.

[3]HASKOPOULOSA,MAROULISG.Interaction Electric Hyperpolarizability Effectsin Weakly Bound H2O,Rg(Rg=He,Ne,Ar,Kr and Xe)Complexes[J].Journalof PhysicsChemistry A,2010,114(33):8730-8741.

[4]HODGESMP,WHEATLEYRJ,HARVEYAH.Intermolecular Potentials and Second Virial Coefficientsof the Water-Neonand Water-Argon Complexes[J].Journalof Chemistry Physics,2002,117(15):7169-7179.

[5]MAKAREWICZ J.Ab Initio Intermolecular Potential Energy Surfaces of the Water-Rare Gas Atom Complexes[J].Journal of Chemistry Physics,2008,129(18):184310-184320.

[6]WENQ,TAGERW.Rotational Spectroscopic and Ab Initio Studiesof the Xe-H2OVan Der Waals Dimer[J].Journal of Physics Chemistry A,2006,110(24):7560-7567.

[7]KUMAS,SLIPCHENKOMN,MOMOSET,etal.Infrared Spectraand Intensitiesof Ar-H2Oand O2-H2OComplexesin the Rangeof theν3Band of H2O[J].Journalof PhysicsChemistry A,2010,114(34):9022-9027.

[8]LIS,ZHENGR,ZHUY,et al.Rovibrational Spectra of the Ar-D2O and Kr-D2O Van Der Waals Complexes in the v2Bend Region of D2O[J].Journalof Molecular Spectroscopy,2012,272(1):27-31.

[9]VANW J,JAGERW.Rotational SpectraoftheKr-H2OVan Der WaalsComplex[J].Journal of Molecular Physics,2000,98(19):1575-1588.

[10]COHEN R C,BUSAROW K L,LEE Y T,et al.Tunable Far Infrared Laser Spectroscopy of Van Der Waals Bonds:the Intermolecular Stretching Vibration and Effective Radial Potentials for Ar-H2O[J].Journalof Chemistry Physics,1990,92(1):169-179.

[11]BULSKIM,WORMERPES.Ab InitioPotential Energy Surfacesof Ar-H2Oand Ar-D2O[J].Journalof Chemical Physics,1991,94(12):8096-8104.

[12]FRASER G T,LOVAS F J,SUENRAM R D.Microwave Spectrum of Ar-H2O:Dipole Moment,Isotopic Studies,and 17O Quadrupole Coupling Constants[J].Journal of Molecular Spectroscopy,1990,144(1):97-112.

[13]GERMANN T C,GUTOWSKY H S.Nuclear Hyperfine Interactions and Dynamic State of H2O in Ar-H2O[J].Journal of Chemical Physics,1993,98(7):5235-5238.

[14]LASCOLAR,NESBITTD J.Slit-jet Near-infrared Spectroscopy and Internal Rotor Dynamics of the Ar-H2O Van Der Waals Complex:An Angular Potential-Energy Surface for Internal H2ORotation[J].Journalof Chemical Physics,1991,95(11):7917-7927.

[15]NESBITTDJ,LASCOLAR.Vibration,Rotation,and Parity Specific Predissociation Dynamicsin Asymmetric OHStretch Excited Ar-H2O:A half Collision Studyof Resonant V-VEnergy TransferinaWeakly Bound Complex[J].Journalof Chemical Physics,1992,97(11):8096-9005.

[16]WEIDAMJ,NESBITTDJ.High Resolution Mid-infrared Spectroscopy of Ar-H2O:The v2Bend Regionof H2O[J].Journal of Chemical Physics,1997,106(8):3078-3040.

[17]COHENRC,BUSAROWKL,LAUGHLINKB,etal.Tunable Far Infrared Laser Spectroscopy of Van Der Waals Bonds:Vibration-Rotation-Tunneling Spectraof Ar-H2O[J].Journal of Chemical Physics,1988,89(8):4494-4511.

[18]SUZUKIS,BUMGARNERRE.Tunable Far-infrared Laser Spectroscopy of Deuterated Isotopomers of Ar-H2O[J].Journalof Chemical Physics,1991,94(1):824-839.

[19]COHENRC,SAYKALLYRJ.Multidimensional Intermolecular Dynamics from Tunable Far Infrared Laser Spectroscopy:Angular-Radial Coupling in the Intermolecular Potential of Argon-H2O[J].Journal of Chemical Physics,1991,95(11):7891-7902.

[20]VERDESD,LINNARTZH.Depletion Modulation of Ar-H2Oina Supersonic Planar Plasma[J].Chemical Physics Letters,2002,355(5-6):538-542.

[21]PATKOWSKI K,KORONA T.Ab Initio Potential Energy Surface and Second Virial Coefficient for He-H2O Complex[J].Journal of Molecular Structure:Theochem,2002,591(1-3):231-243.

[22]HODGES M P,WHEATLEY R J,HARVEY A H.Intermolecular Potentials and Second Virial Coefficients of the Water-neon and Water-argon Complexes[J].Journal of Chemical Physics,2002,117(15):1397-1408.

[23]COHENRC,SAYKALLYRJ.Extending the Collocation Method to Multidimensional Molecular Dynamics:Direct Determination of the Intermolecular Potentialof Argon-waterfromTunableFar-infrared Laser Spectroscopy[J].Journal of Physics Chemistry,1990,94(20):7991-8000.

[24]COHEN R C,SAYKALLY R J.Determination of an Improved Intermolecular Global Potential Energy Surface for Ar-H2O from Vibration-rotation-tunneling Spectroscopy[J].Journalof Chemical Physics,1993,98(8):6007-6023.

[25]CHALASINSKIG,MSZCZEM.Ab Initio Study of the Intermolecular Potential of Ar-H2O[J].Journal of Chemical Physics,1991,94(4):2 807-2817.

[26]RAGHAVACHARI K,TRUCKS G W,POPLE J A,etal.A Fifth-order Perturbation Comparison of Electron Correlation Theories[J].Chemical Physics Letters,1989,157(6):479-483.

[27]WOONDE,DUNNINGTH.Gaussian Basis Setsfor Usein Correlated Molecular Calculations.III.The Atoms AluminumThrough Argon[J].Journalof Chemical Physics,1993,98(2):1358-1375.

[28]CHALASINSKIG,SZCZEM.State of the Artand Challenges of the Ab Initio Theory of Intermolecular Interactions[J].Chemical Reviews,2000,100(11):4227-4252.

[29]BOYS S F,BERNARDI F.The Calculation of Small Molecular Interactions by the Differences of Separate Total Energies:Some Procedureswith Reduced Errors[J].Journal of Molecular Physics,1970,19(4):553-566.

[30]WERNERHJ,KNOWLESPJ,MANBYFR,etal.APackageof Ab Initio Programs[EB/OL].[2017-08-10].http://www.molpro.net.

[31]PRESSWH,FLANNERYBP.Numerical Recipesin Fortran90:the Art of Scientific Computing[M].Cambridge:CambridgeUniversity Press,1996.

[32]MATSUSHIMA F,MATSUNAGA M.Frequency Measurement of Pure Rotational Transitions of D2O from 0.5 to 5 THz[J].Journal of Molecular Spectroscopy,2001,206(1):41-46.

[33]ZWARTE,MEERTSWL.The Submillimeter Rotation-tunneling Spectrum of Ar-D2Oand Ar-NH3[J].Chemical Physics,1991,151(3):407-418.

Theoretical Calculations for Bound State of Ar-D2O Complex

WANG Shen-hao1,FENG Er-ying2,TAO Zong-ming1,SHAN Hui-hui1,MA Xiao-min1
(1.Department of Basic Sciences,Army Academy of Artillery and Air Defense Force,Hefei,Anhui 230031,China;2.College of Physics and Electronic Information,Anhui Normal University,Wuhu,Anhui 241000,China)

We report a new three-dimensional potential energy surface for the Ar-D2O complex with the D2O monomer fixed at its experimental averaged structure.The ab initio calculations are carried out by the coupled-cluster singles and doubles level with noniterative inclusion of connected triples[CCSD(T)]method with a large basis set supplemented with bond functions(3s3p2d2f1g).The potential energy surface(PES)has a global minimum at R=6.91a0，θ=71.25°，φ=0.0°with a well depth of 138.7 cm-1,corresponding to a planar configuration.In addition,two first-order and one second-order saddle points were also identified.To facilitate the following calculation of bound states,the potential is further expanded as a spherical expansion,and for the radial coordinate R,the cubic spline interpolation method was employed for expanded coefficients vlm(R).we calculated the bound state energies(J≤2)by solving the Schrdinger equation.The theoretical frequencies for microwave transition and vibration–rotation–tunneling(VRT)spectra transition were also investigated.The calculated frequencies of Ar-D2O complex are in good agreement with the experimental results.

Ar-D2O complex;three-dimensional potential energy surface;microwave spectra;vibration-rotation-tunneling spectra

O469

A

1673-1972（2017）06-0019-08

2017-09-05

国家自然科学基金（11374014）

王申浩（1989-），男，安徽霍山人，助教，硕士，主要从事计算分子光谱学研究.

（责任编辑 钮效鹍）