相变蓄热材料导热系数对太阳能通风墙性能的影响

穆林， 雷勇刚， 宋翀芳， 程远达

(太原理工大学 环境科学与工程学院， 山西 太原 030024)

相变蓄热材料导热系数对太阳能通风墙性能的影响

穆林， 雷勇刚， 宋翀芳， 程远达

(太原理工大学 环境科学与工程学院， 山西 太原 030024)

通过对相变蓄热型太阳能烟囱模型通风蓄放热变化过程的计算，分析比较不同相变蓄热墙导热系数对太阳能烟囱性能的影响.计算结果表明：吸热板最大表面温度随着相变蓄热墙导热系数的增大越接近相变蓄热墙的相变温度；蓄热阶段，入口平均风速随着相变蓄热墙导热系数的增大而减小；放热阶段，入口平均风速随着相变蓄热墙导热系数的增大反而越大；相变蓄热墙导热系数越大，蓄热型太阳能烟囱系统16 h的累计通风量越高，但在导热系数增大到0.66 W·(m·K)-1后，再增大材料导热系数，累计通风量几乎不再增加.

太阳能烟囱； 相变材料； 蓄热墙； 通风； 导热系数

太阳能烟囱是利用太阳能加热空气产生烟囱效应，从而促进通风效果的装置，它具有节能效果显著、与建筑结合方便、初投资相对较少等优点.然而，太阳能易受气候环境影响，限制了太阳能烟囱的发展应用.国内外学者对太阳能烟囱相变蓄热的特性进行了许多研究[1-9].Arkar等[1]提出一种相变蓄热模块(LHTES)进行建筑自然冷却通风，对不同气候地点自然冷却潜力进行分析.Stritih等[2]设计结合黑色石蜡相变材料的太阳能烟囱，相变材料储存的热量被用来加热和通风.Amori等[3]对具有相变温度为65.6 ℃石蜡的太阳能烟囱开展了实验和数值研究.David等[4]建立具有相变材料的物理模型，对自然、强制和混合对流条件下进行计算.Liu等[5]对具有不同厚度的双层Na2CO3·H2O蓄热墙的太阳能烟囱系统进行恒热流实验.Giacia等[6-7]对双层通道结合SP-22相变材料进行了实验研究，结果表明,应用PCM夹层对于建筑的热效果提高明显.李风雷等[8]利用TRNSYS软件,模拟计算以R141b为制冷剂的蓄热型太阳能喷射制冷系统在夏季典型日的性能.Li等[9-10]对具有42 ℃相变温度石蜡的太阳能烟囱系统进行实验测试，研究稳定条件下,热流密度和石蜡层导热系数对太阳能烟囱系统热效率和通风传热特性的影响.吴彦廷等[11]建立了二维相变蓄热太阳能烟囱数理模型，分析空气通道宽度对太阳能相变蓄热集热墙系统热特性的影响.李永财[12]研究了结合相变蓄热材料的太阳能通风屋顶系统，结果显示9月份60 ℃的日间通风量较大，晚间的40 ℃的通风量较大.卢军等[13]对具有相变温度的相变材料的太阳能通风屋顶进行数值模拟，获得不同相变温度下,系统的夜间通风量的变化规律.王元明等[14]以石蜡为材料,制造出针对于太阳能烟囱应用复合相变材料，结果表明,碳纳米管的添加可以有效提高相变材料的热导率和相变过程的传热速率.虽然对太阳能烟囱结合相变蓄热的研究较多，但是蓄热墙导热系数对太阳能烟囱系统的性能影响的成果比较匮乏.因此，本文建立了相变蓄热型太阳能烟囱系统的三维非稳态模型，并用文献[3]的实验结果验证了其准确性，研究不同蓄热墙导热系数对太阳能烟囱系统通风放热性能的影响.

1 物理模型

(a) 物理模型 (b) 计算区域图1 相变蓄热型太阳能烟囱系统(单位：mm)Fig.1 Phase change and thermal storage type of solar chimney system (unit:mm)

相变蓄热型太阳能烟囱系统由半透明玻璃盖板、吸热板、相变蓄热材料板、绝热保温板组成，其物理模型如图1(a)所示.其工作原理：半透明玻璃盖板和吸热板之间形成空气通道，空气由入口进入通道，被吸热板加热后从出口排出，强化了烟囱系统自然通风.相对于传统的太阳能烟囱系统，本模型采取了相变蓄热墙，通过蓄热材料的相变蓄热可有效提高系统的蓄热效果，延长系统放热时间.该结构高度为2 m，宽度为1 m，深度为0.25 m，高深比为10∶1[15]，其中相变材料层厚度为0.05 m，玻璃盖板和吸热板厚度均为0.004 m.本模型X为正南方向，计算区域如图1(b)所示.

2 数学模型

数值模拟假设如下:1) 工作流体为不可压缩牛顿流体；2) 流体密度只与温度有关，满足Boussinesq假设；3) 沿着吸热板边缘的热传导忽略不计；4) 相变材料相变温度为定值，固液相物性参数一致，无固液相分离；5) 忽略接触热阻.使用有限容积法求解控制方程，模拟采用RNGk-ε湍流模型、融化/凝固模型和离散坐标(DO)模型，速度与压力之间的耦合采用SIMPLE算法，对流项的离散格式使用二阶迎风格式，离散方程的求解应用亚松弛TDMA算法.

1) 连续性方程为

2) 动量方程为

3) 能量方程为

4)k-方程为

5)ε-方程为

式(5)～(7)中：ui为xi方向上的平均速度矢量；xi为坐标；p为平均压力；t为非稳态时间；vt，v分别为絮流和层流黏滞系数；gi为i方向的重力加速度；β为空气膨胀系数；T，Tin为平均温度和室内温度；Γ为广义扩散系数；k为湍流脉动动能；ε为流体脉动动能的耗散率；C1，C2为经验系数；Gk为湍流动能的产生项；Pr为Prandel数；σk，σε，σt取经验值.

6) 相变方程为

7) 发射和散射方程为

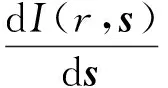
式(8),(9)中：H为焓值；r材质所在位置；s为直射方向矢量；s′为散射方向矢量；δ为散射系数；n为折射系数；α为吸收系数；Ф为相位函数；Ω为空间立体角.

3 边界条件和物性参数

3.1边界条件

1) 太阳辐射得热.太阳辐射强度是影响太阳能烟囱相变蓄热的主要因素.通过给定时间、日期和位置的太阳光束方向和辐射照度，对法向直接辐照应用ASHRAE手册的晴朗天气条件的方程为Edn=A/exp(B/sinβ)，对漫射辐射的表达式为Ed=CYEdn，计算得到的参数作为太阳射线跟踪算法半透明边界条件的输入条件.玻璃盖板边界条件：玻璃盖板外边界采取第三类边界条件，对流换热系数h=4 W·(m2·K)-1，外界空气温度取夏季通风温度为300 K.

2) 其他壁面面边界条件.吸热面采取无内热源耦合边界，绝热木板为绝热边界.

3) 出入口边界条件.入口采取压力入口边界条件，入口空气温度取太原夏季通风温度300 K,而出口采取压力出口边界条件.

4) 初始条件.初始温度为300 K，初始相对压力为0，初始速度为0.

3.2物性参数

玻璃盖板(4 mm玻璃)、吸热板(4 mm钢板)、空气和相变石蜡的物性参数，如表1所示.表1中：ρ为密度；λ为导热系数；cp为比热容；α为吸收率；θ为发射率；τ为透射率；t为相变温度；Q为相变潜热.

表1 材料的物性参数Tab.1 Physical properties of material

4 网格独立性考核与模型有效性验证

由于模型结构形式比较规则，计算区域采用结构化正六面体网格.图2为计算网格(Z轴方向截面图)，上面为相变材料，下面为空气通道.为了使计算结果准确且节省计算资源，进行了网格独立性考核.对5套不同的网格下10：00的入口风速进行计算，网格7 608，13 639，56 724，107 642，210 378时的入口平均风速分别为2.210，1.320，0.253，0.224，0.223 m·s-1.可以看出，第4套和第5套网格的计算偏差小于1%，因此，得到了网格无关的独立解.考虑到计算精度和计算速度要求，以第4套网格作为所有数值计算网格，其网格数为107 642.

图2 太阳能烟囱相变蓄热系统网格划分Fig.2 Grid generation of phase change and thermal storage type solar chimney system

图3 模拟结果与实验数据比较Fig.3 Simulation results compared with experimental data

为了验证该模型，根据文献[3]实验参数，建立970 mm×150 mm×2 000 mm的相变蓄热型太阳能烟囱模型.其相变材料层厚度为40 mm，室外温度和室外太阳辐射强度与文献[3]一致.吸热板平均温度模拟结果与实验结果比较,如图3所示.

由图3可知：模拟计算与实验所测温度随时间变化趋势基本吻合，最大温度都是在13:00；放热阶段的偏差较大，主要是因为模拟计算时忽略了接触热阻和能量损耗.由图3还可以看出：本模拟计算结果与文献[3]的实验结果误差在±5%以内，表明本模型的可靠性.

5 实验结果与分析

5.1吸热板表面平均温度与时间的变化关系

图4 吸热板表面温度随时间变化Fig.4 Endothermic board surface temperature over different times

不同蓄热墙导热系数下，吸热板表面平均温度随时间的变化关系，如图4所示.由图4可知：由于太阳的辐射，吸热面的温度均从初始时刻的300 K开始增大，到13：00时达到最大值，然后开始下降.这与太阳入射辐射13：00时出现最大值相对应.由图4还可知：吸热板表面最大温度随着相变蓄热墙导热系数的减小反而越大，采用1.10 W·(m·K)-1相变蓄热墙时，吸热板表面的最大温度为317.62 K，而采用0.33 W·(m·K)-1相变蓄热墙时，吸热板表面最大温度却为322.2 K.这是由于相变材料达到相变温度后开始相变蓄热，导热系数大时,吸热板与相变材料之间的传热热阻比较小，较多的热量会被相变材料储存，对同样的入射辐射热流，吸热板表面温度就比较低.

另外，相变蓄热墙导热系数越低,吸热板蓄热和放热时的温差就越大，随着相变材料导热系数的变大，这种差别逐渐降低直至消失，最终都会等于相变温度.此时,蓄热墙的储存热量达到最大值，导热系数为0.33 W·(m·K)-1的相变材料吸热板最大温度与相变温度的差值为6.2 K，而导热系数为1.10 W·(m·K)-1时仅为1.62 K.由此可以看出，图4中20：00时刻都有一个明显的转折点.这是因为太阳入射辐射在20：00降为0，系统进入单纯放热阶段.

5.2入口平均风速与时间的变化关系

不同蓄热墙导热系数下,入口平均风速(v)随时刻的变化关系，如图5所示.由图5可知：不同蓄热墙导热系数下，系统入口平均风速在到达13：00以前均是不断增大的，到13：00时均达到最大值，且相变蓄热墙导热系数越小，入口平均风速越大，这与吸热面温度相对应的；在18：00以后，相变蓄热墙进入放热阶段.由图5还可知：导热系数越大，入口平均风速越大，反之则越小.这是由于导热系数小，相变蓄热墙传递到空气中的热流就会少；而导热系数大，相变蓄热墙传递到空气中的热流就会越大.但是，当导热系数增加到0.66 W·(m·K)-1时，再增加，效果就会越来越不明显；当导热系数为1.10 W·(m·K)-1时，几乎和0.66 W·(m·K)-1相同.

不同通风时间内的累计通风量(Q)，如图6所示.由图6可知：在通风12 h以前，导热系数越大,累计通风量越大;通风12 h以后，导热系数越大,累计通风量反而越小;而且在通风12 h时，不同导热系数下累计通风量几乎相等.但是,当导热系数超过0.66 W·(m·K)-1以后,再增大导热系数对累计通风量几乎不再有影响.

垂直Y轴中心面局部速度流图，如图7所示.由图7可知：在出口处有回流现象.

图5 入口平均风速随时间变化 图6 不同通风时间内累计通风量 Fig.5 Entrance average wind speed change over time Fig.6 Total ventilation rate over different times

5.3吸热板中心温度沿高度方向的变化关系

吸热板中心温度沿高度方向的变化关系，如图8所示.由图8可知：吸热板中心温度在13:00沿高度方向均不断增大，且高度在0.2～0.8 m和1.2～1.8 m时变化趋势比较大，高度在0.8～1.2 m时变化趋势变得比较平缓.另外，导热系数越小，吸热板温度越高，导热系数越大，吸热板温度越低，且随着高度的增加，这种差别越来越大.由图8还可知：在高度为0.2 m时，导热系数0.33,1.10 W·(m·K)-1对应的温差几乎为0 K;在高度为1.0 m时，导热系数0.33和1.10 W·(m·K)-1对应的温差为6.67 K;而在高度为1.8 m时，导热系数0.33和1.10 W·(m·K)-1对应的温差则增大为9.8 K.

此外，随着导热系数的增大，吸热板中心温度沿高度方向的变化越来越平缓，而且当导热系数增大到0.66 W·(m·K)-1后,再增大导热系数，吸热板中心温度沿高度方向的变化越来越接近相变温度.这和图4结论相同.

图7 中心面局部速度流场图 图8 吸热板中心温度沿高度方向的变化关系 Fig.7 Local flow field at core surface Fig.8 Heat absorbing plate core temperature along height direction

6 结论

建立太阳能烟囱相变蓄热通风系统的三维数理模型，并对太原市7月15日8：00-24:00的蓄放热和通风性能随时间变化的关系开展数值模拟研究，得到以下3个主要结论.

1) 相变蓄热墙导热系数越低，吸热板蓄热和放热时,温差就越大；随着相变蓄热墙导热系数的变大，这种差别逐渐降低直至消失，最终等于相变温度，此时,蓄热墙储存热量达到最大值；当相变蓄热墙导热系数增大到0.66 W·(m·K)-1以后，再增大导热系数，吸热板表面温度变化变得越来越弱.

2) 蓄热阶段入口平均风速随相变蓄热墙导热系数增大而增大，且均在13：00出现最大风速；放热阶段入口平均风速随相变蓄热墙导热系数增大反而减小.导热系数低的相变蓄热墙热阻比较大，白天蓄热阶段存储的热量较少，更多的热量用于通风使入口风速较大；晚上放热阶段放出的热量较少，使入口风速变得较小.在通风12 h以前，导热系数越大累计通风量越大;通风12 h以后，导热系数越大累计通风量反而越小，而且在通风12 h时，不同导热系数下累计通风量几乎相等.但是,当导热系数超过0.66 W·(m·K)-1以后,再增大导热系数后,对累计通风量几乎不再有影响.

3) 吸热板中心温度沿高度方向不断增大，而且吸热板中心温度沿高度方向的变化随着导热系数越大越来越平缓.当导热系数增大到0.66 W·(m·K)-1后,再增大导热系数，吸热板中心温度沿高度方向的变化越来越接近相变温度.

[1] ARKAR C，MEDVED S.Free cooling of a building using PCM heat storage integrated into the ventilation system[J].Solar Energy，2007，81(9):1078-1087.DOI:10.1016/j.solener.2007.01.010.

[2] STRITIH U，NOVAK P.Solar heat storage wall for building ventilation[J].Renewable Energy，1996，8(1/2/3/4):268-271.DOI:10.1016/0960-1481(96)88860-4.

[3] AMORI K E，MOHAMMED S W.Experimental and numerical studies of solar chimney for natural ventilation in Iraq[J].Energy and Buildings，2012，47(4):450-457.DOI:10.1016/j.enbuild.2011.12.014.

[4] DAVID D，KUZNIK F,ROUX J J.Numerical study of the influence of the convective heat transfer on the dynamical behaviour of a phase change material wall[J].Applied Thermal Engineering，2011，31(16):3117-3124.DOI:10.1016/j.applthermaleng.2011.04.

[5] LIU Bin,LI Peng,MA Xiaoyan,etal.Chimney effect of solar hybrid-double wall with different thickness PCM of Na2CO3·10H2O[J].Energy Procedia,2015,75:521-526.DOI:10.1016/j.egypro.2015.07.443.

[6] GRACIA A D,NAVARRO L,CASTELL A,etal.Experimental study of a ventilated facade with PCM during winter period[J].Energy and Buildings,2012,58(2):324-332.

[7] GRACIA A D,NAVARRO L,etal.Solar absorption in a ventilated facade with PCM: Experimental results[J].Energy Procedia,2012,30(1):986-994.DOI:10.1016/j.enbuild.2012.10.026.

[8] 李风雷,任艳玲.典型气象日蓄热型太阳能喷射制冷系统性能分析[J].华侨大学学报(自然科学版),2014,35(2):185-190.DOI:10.11830/ISSN.1000-5013.2014.02.0185.

[9] LI Yongcai,LIU Shuli.Experimental study on thermal performance of a solar chimney combined with PCM[J].Applied Energy,2014,114:172-178.DOI:10.1016/j.apenergy.2013.09.022.

[10] LI Yongcai,LIU Shuli,SHUKLA A.Experimental analysis on use of thermal conductivity enhancers (TCEs) for solar chimney applications with energy storage layer[J].Energy and Buildings,2016,116:35-44.DOI:10.1016/j.enbuild.2015.12.049.

[11] 吴彦廷，周国兵.太阳能相变蓄热集热墙二维非稳态模型及分析[J].太阳能学报,2010，33(6):949-952.

[12] 李永财.太阳能通风技术结合相变蓄热材料自然通风效果实验研究[D].重庆:重庆大学,2009:1-101.

[13] 卢军，赵娟,黄光勤,等.太阳能蓄能通风系统理论模型[J].土木建筑与环境工程,2012，34(3):64-74.

[14] 王元明.石蜡/碳纳米管复合相变材料的性能研究[J].现代化工，2015，35(1):130-134.

[15] RYAN D，BUREK S A M.Experimental study of the influence of collector height on the steady state performance of a passive solar air heater[J].Solar Energy，2010，84(9):1676-1684.DOI:10.1016/J.SOLENER.2010.05.018.

(责任编辑： 黄晓楠英文审校： 刘源岗)

EffectofThermalConductivityonPerformanceofSolarChimneyWithPhaseChangeAccumulator

MU Lin， LEI Yonggang， SONG Chongfang， CHENG Yuanda

(School of Environment Science and Engineering， Taiyuan University of Technology， Taiyuan 030024， China)

The influence of different thermal conductivities of phase change and thermal storage wall on the performance of solar chimney was analyzed and compared through the calculation of the ventilation and heat storage or release change process of the phase change and thermal storage type of solar chimney model. The results show that the maximum temperature of the heat absorber plate is more close to the phase change temperature with the increase of the thermal conductivity of the phase change and heat storage wall. The average inlet wind velocity reduces with the increase of the thermal conductivity for the process of heat storage， while increases for the process of heat release. The higher the thermal conductivity of the phase change and thermal storage wall is, the higher the cumulative ventilation in 16 hours of the regenerative solar chimney system will be.But when the thermal conductivity is increased to 0.66 W·(m·K)-1, the cumulative ventilation has almost no increase even if increasing the thermal conductivity of the material.

solar chimney； phase change materials； thermal storage wall； ventilation; thermal conductivity

10.11830/ISSN.1000-5013.201612040

TU 834

A

1000-5013(2017)06-0830-06

2016-12-20

雷勇刚(1976-)，男，教授，博士，主要从事低功耗强化传热技术、供热技术和建筑节能技术的研究.E-mail:yongganglei@gmail.com.

国家自然科学基金资助项目(51106103, 51408391)