构造相似三角形破解一类最值题

吴智勇

构造相似三角形破解一类最值题

吴智勇

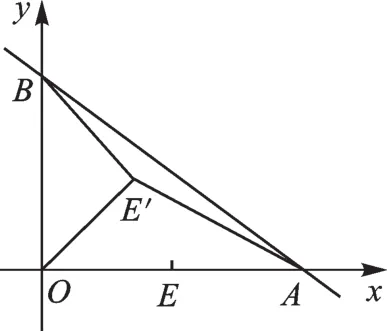
图1

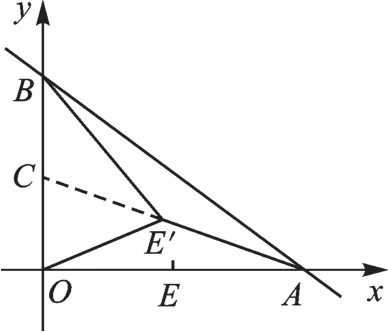
图2

【思路突破】首先理解题目，弄清题目已知什么，用自己的语言叙述题目条件并与学过的知识联系起来.题目已知直线AB：与x轴交于点A，与y轴交于点B，告诉我们点A（4，0），B（0，3）.点E（2，0）在x轴上，将线段OE绕点O逆时针旋转得到OE′，则说明点E′是以原点为圆心，2为半径的圆上的动点.题目要求的最小值，这个问题以前没有见过，是个新问题.与这个问题相似的是求两条折线段的和的最小值，那么我们能不能将转化成某一条线段，从而将新问题转化为我们熟悉的问题？又该从何处着手将B转化成系数为1的某一条线段？先进行直觉判断，题中的直线AB与y轴交于点B，其中OB=3，OE′=OE=2，比值恰好是由比值猜想是否可以构造一对相似比为的相似三角形△COE′∽△E′OB？试试在y轴上取点C，连CE′，则这样欲寻找的E′A的最小值就转化为寻找CE′+E′A的最小值，由于点A、C是定点，因此只要点A、E′、C三点共线时就能取得最小值，E′A≥AC，而

【解后反思】解题要有灵感，不可呆板，题目要求的最小值，这是一个以前没有见过的新问题.解题的切入口是联想以前做过的问题，将转化成另一条线段CE′，从而将没有见过的问题转化为已经解决的问题.转化的方法是由题目条件得出OB=3，O′E=OE=2，联想比值从而将我们的思路往构造相似三角形的方向上引导，转化是解题的根本手段.

【同类题巩固】

1.如图3，在Rt△ABC中，∠ACB=90°，CB=4，CA=6，⊙C的半径为2，点P为⊙C的一动点，连接AP、BP，则的最小值为

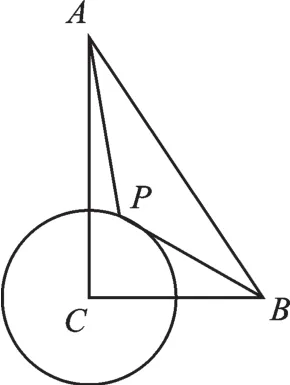
图3

【解析】解决问题的关键是将PB转化为系数为1的某一线段，因此需要找一个定点，构造一对相似三角形来转化.问题转化为“两定一动”，当三点共线时得到线段和的最小值.考虑到BC=2PC，在CB上取点D，使CD=1，连接PC、PD，如图4，则，当A、P、D三点共线时等号成立.，故的最小值为

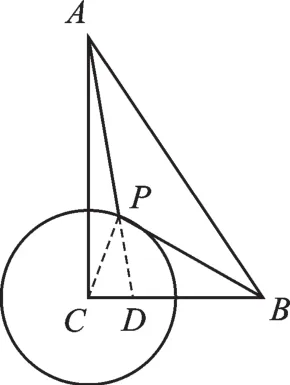
图4

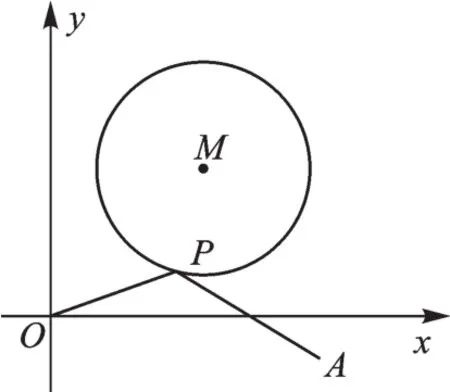
图5

【解析】考虑到OM=2PM，在OM上找一点B（3，3），连BP，则，由，所以PA）≥2BA，当A、P、B三点共线时等号成立.根据勾股定理得AB=5，故PO+2PA的最小值为10.

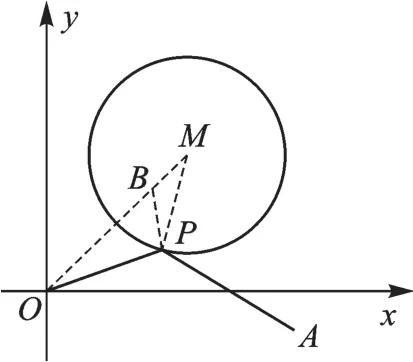
图6

3.已知：⊙B的圆心为B（1，1），交y轴于C（0，3），动点P在⊙B上，连接PC、PO.则2PC+5PO的最小值为.

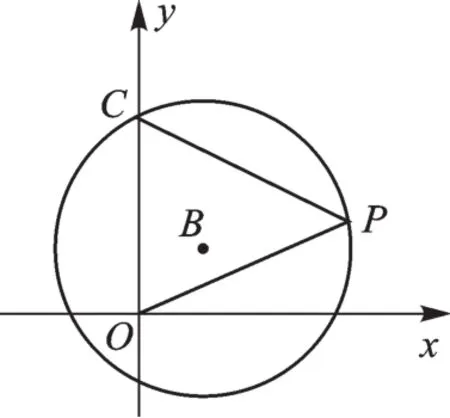
图7

【解析】⊙B的半径为，如图8，连接BP，BO，在BO延长线上取点，当C、P、D三点共线时等号成立.故PC+5PO的最小值为

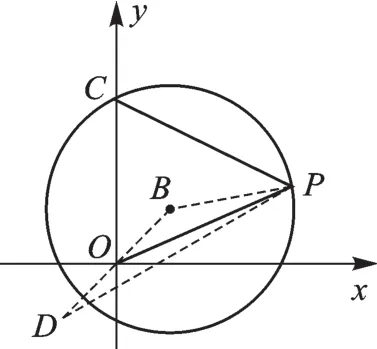
图8

（作者单位：江苏省东台市实验中学）