活用基本型学好相似形

赵军（特级教师）

活用基本型学好相似形

赵军（特级教师）

在运用相似三角形解决问题的过程中，我们经常会遇到一些较为复杂的几何图形，如何从中找出相似三角形的“基本型”往往成为解题的关键，下面仅以常见的一些相似三角形的基本图形为例进行归类分析，希望对大家的学习有所帮助.

一、“A”型

在三角形的相似模型中，有一类像大写字母“A”的图形，我们称之为“A型”，在具体图形中我们又将其分为“正A型”和“斜A型”两种.

例1如图1，在△ABC中，点D、E分别在AB、AC上，且DE∥BC，若AD=5，BD=10，AE=3，则CE的长为.

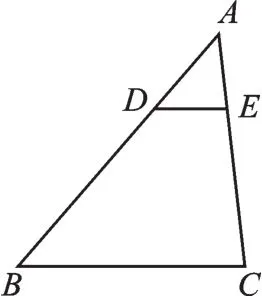
图1

【思路点拨】由DE∥BC可得△ADE∽△ABC，所以，设CE=x，则，解之得：x=6，所以CE的长为6.如图1中的△ADE与△ABC相似可形象地称之为“正A型”相似.

变式1如图2，在△ABC中，点D、E分别在AB、AC上，且∠AED=∠B，若AD=3，BD=10，AE=5，则CE的长为.

【思路点拨】由∠AED=∠B，∠A=∠A可得△AED∽△ABC，所以，设CE=x，则，解之得，所以CE的长为如图2中的△AED与△ABC的相似可形象地称之为“斜A型”相似.

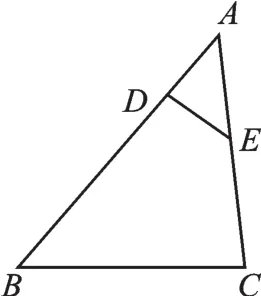
图2

变式2如图3，在△ABC中，AC=9，AB=6，点E在AC上，且AE=3，点D在AB上，连接ED.若△AED与△ABC相似，则AD=.

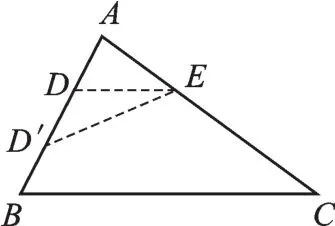
图3

【思路点拨】题目给出的条件是△AED与△ABC相似，没有明确对应关系，所以要分情况讨论（.1）当DE∥BC时，△ADE∽△ABC，属于“正A型”相似，此时有，即所以AD=2；（2）当∠AED′=∠B时，△AD′E∽△ACB，属于“斜A型”相似，此时有即，所以AD′=4.5.故AD=2或4.5.

归纳小结学习相似三角形一定要注意对应关系，在“A型”相似中，有“正A型”相似和“斜A型”相似，当题目给出的条件只交待一个三角形与另一个三角形相似，而不明确字母的对应关系时，一定要注意分类讨论，大家在学习过程中一定要注意哦！

小试牛刀

1.如图4，路灯距离地面8米，身高1.6米的小明站在距离灯的底部（点O）20米的A处，则小明的影子AM长为米.

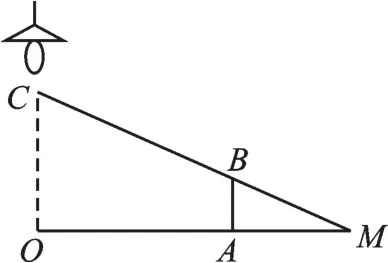
图4

【授人以渔】抓住△ABM∽△OCM（“正A型”相似），利用相似三角形的对应边成比例，列出方程，可求出小明的影长.

2.如图5，PB、PD分别与⊙O相交于A、B、C、D四点，已知PA=2，PB=7，PC=3，则CD=.

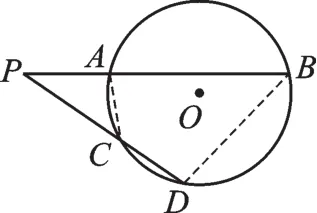
图5

【授人以渔】连接AC、BD，容易证得△PAC∽△PDB（“斜A型”相似），所以，分别代入PA、PB、PC的值可求出PD的长，然后用PD-PC即可求出CD.

二、“8”型

在三角形的相似模型中，还有一类像数字“8”的图形，我们称之为“8型”.在具体图形中我们又将其分为“正8型”和“斜8型”.

例2如图6，AB、CD相交于点O，AD∥BC，若OD=2，OC=3，AD=4，则BC的长为.

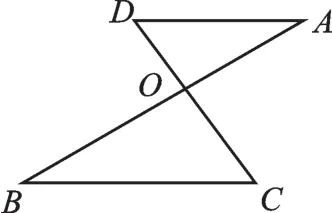
图6

【思路点拨】由AD∥BC可得△ADO∽△BCO，所以，即，解之得：BC=6，所以BC的长为6.如图6中的△AOD与△BOC相似可形象地称之为“正8型”相似.

变式1如图7，AB、CD相交于点O，且∠D=∠B，若OD=6，OC=4，AB=11，且OB＞OA，则OA=，OB=.

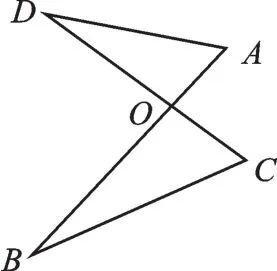
图7

【思路点拨】由∠D=∠B，∠AOD=∠COB得△AOD∽△COB，所以，设OA=x,则OB=11-x，所以，解之得：x=8或3，因为OB＞OA，所以OA=3，OB=8.

变式2如图8，CD、BE相交于点A，AC=2cm，AB=3cm，AE=4cm，AD=8cm，点F为线段AD上一点，若△AEF与△ABC相似，求AF的值.

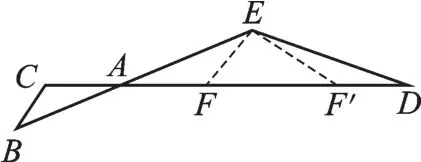
图8

【思路点拨】△AEF与△ABC相似，并未指明对应关系，需要分情况进行讨论，当EF∥BC时，△AEF∽△ABC，属于“正8型”相似，此时，所以；当∠AEF=∠C时，△AEF∽△ACB，属于“斜8型”相似，此时，所以AF=6.综上，AF的值为

归纳小结学习相似一定要注意字母与字母、线段与线段之间的对应关系，在“8型”相似中，有“正8型”和“斜8型”两种相似，当题目给出的条件叙述为：一个三角形与另一个三角形相似，一定要注意线段的对应关系，别忘了分情况讨论！

小试牛刀

1.如图9，AB∥GH∥CD，点H在BC上，AC与BD交于点G，AB=2，CD=3，则GH的长为

.

1.黄油室温软化后用刮刀搅拌顺滑。2.水和砂糖加热至103度，蛋液打至鱼眼泡形状。3.边快速打发蛋液边缓缓倒入糖水。4.持续打发至蛋液恢复常温后，一次性将蛋液倒入黄油中打均匀。5.分次将黄油加入板栗蓉中混匀即可。

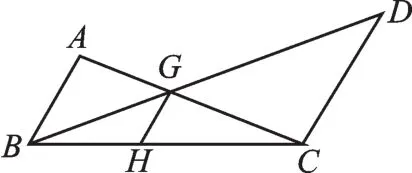
图9

【授人以渔】由AB∥CD，得“正8型”相似：△ABG∽△CDG，所以，再由GH∥CD得“正A型”相似：△BHG∽△BCD，所以，从而问题得解.其关键是抓住平行，利用两次相似，且两次相似比中都有线段BG进行过渡.

2.如图10，在平行四边形ABCD中，E、F分别是边AD、CD上的点，连接BE、AF，它们相交于点G，延长BE交CD的延长线于点H，则图中的相似三角形共有（）.

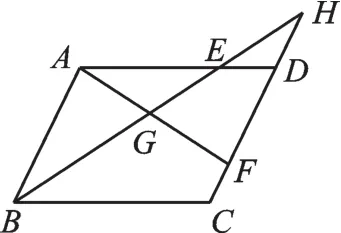
图10

A.2对B.3对C.4对D.5对

【授人以渔】抓住平行四边形的两组对边分别平行，可分别找出“8型”和“A型”相似.由AB∥CH可得“正8型”相似：△ABG∽△FHG、△ABE∽△DHE；由DE∥CB可得“正A型”相似：△DHE∽△CHB；由相似的传递性得：△ABE∽△CHB.所以选C.

三、“K”型

在三角形的相似模型中，除了“A型”“8型”，还有一类像字母“K”的相似图形，我们称之为“K型”相似.

例3如图11，在△ADE和△BCE中，AD⊥AB，BC⊥AB，点E在AB上，且CE⊥DE，若AD=，BE=1，AE=2，则BC的长为.

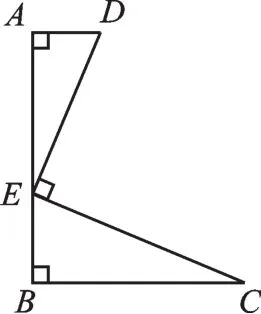
图11

【思路点拨】先证得△DAE∽△EBC，再运用相似三角形的对应边成比例列出方程求BC的值.具体思路如下：由CE⊥DE得：∠AED+∠BEC=90°，由BC⊥AB得：∠C+∠BEC=90°，所以∠AED=∠C，因为∠A=∠B=90°，所以△DAE∽△EBC，所以，解之得：

变式1如图12，在边长为9的等边三角形ABC中，BD=3，∠ADE=60°，则AE的长为

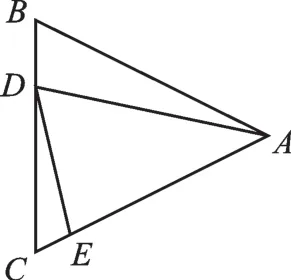
图12

【思路点拨】先证得△ABD∽△DCE，再运用相似三角形的对应边的比列出方程求解.

变式2如图13，在四边形ABCD中，P为AB上一点，当∠DPC=∠A=∠B=θ时，求证：AD∙BC=AP∙BP.

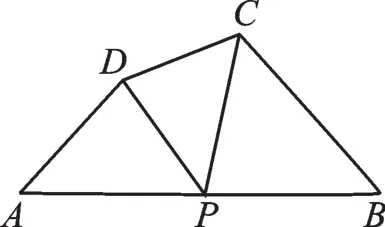
图13

【思路点拨】证明AD∙BC=AP∙BP即需要证明，只需证得△APD∽△BCP，由平角的定义得：∠APD+∠CPB=180°-θ，在△APD中，∠APD+∠PDA=180°-θ，所以∠PDA=∠CPB，因为∠A=∠B，所以△APD∽△BCP，从而得证.

归纳小结“K型”相似的关键是具备这样的条件：在一条直线上有3个角相等，简称“一线三等角”.证明相似时利用平角和三角形的内角和均为180°证得一组角相等，加上条件中的另一组角相等，从而得到相似，并用相似三角形的性质解决问题.

小试牛刀

1.如图14，已知△ABC和△DEF均为等腰直角三角形，BC=AC、DE=FE，∠C=∠E=90°，D为AB边上的一点，将△DEF绕点D旋转，使DF、DE分别交AC、BC于点G、H，求证：AD∙BD=BH∙AG.

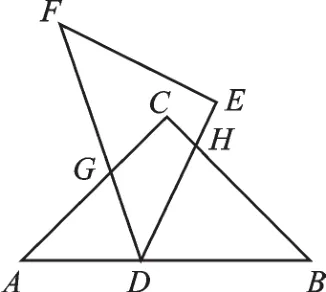
图14

【授人以渔】欲证AD∙BD=BH∙AG，即需要证明，由这个比例式可知，需要找△ADG∽△BHD，根据题目给出的条件可知∠A=∠B=∠GDH=45°，具备一条直线上有3个相等的角，可证得它们相似.

2.如图15，在x轴的上方，直角∠BOA绕原点O按顺时针方向旋转，若∠BOA的两边分别与函数y=-、y=的图像交于B、A两点，则

∠OAB的大小的变化趋势为（）.

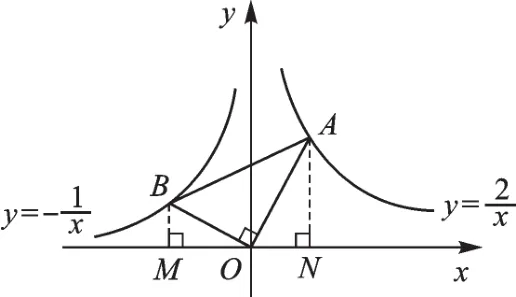
图15

A.逐渐变小B.逐渐变大

C.时大时小D.保持不变

【授人以渔】因为，所以∠OAB的大小是否变化，要看的值是否发生变化，分别过点A、B作AN、BM垂直于x轴，垂足分别为N、M，构造“K型”相似：△BOM∽△OAN，可将转化为，结合两个反比例函数的解析式分别求出的值保持不变，即∠OAB的大小不变.

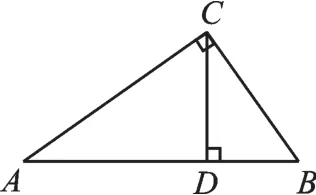
图16

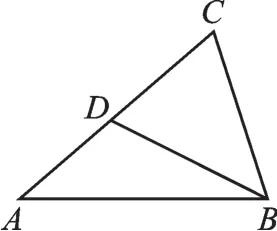
图17

相似三角形的基本型还有很多，如图16中的“母子型”相似（由∠ACB=∠CDB=90°得△ACD∽△CBD∽△ABC，又可得：CB2=BD∙BA、CA2=AD∙AB、CD2=DA∙DB）；

如图17中的“共边型”相似（△BCD与△ACB共边BC，且△BCD∽△ACB等价于BC2=CD∙CA）；

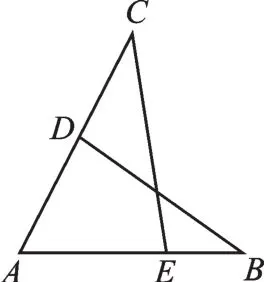
图18

如图18中的“共角型”相似（△ABD与△ACE有公共角∠A，再添加一个条件即可得相似）等.各位同学可以根据自己的学习经验进行归纳，不断小结，并在解决问题的过程中善于发现模型，在模型积累的基础上做到灵活运用，有效提升解决问题的能力.总而言之，要想学好相似形，首先要抓住基本型.

（作者单位：江苏省东台市新街镇中学）