由抛物线上的点生成的几何问题

张彩云

由抛物线上的点生成的几何问题

张彩云

二次函数在初中数学学习中占有重要地位，分析各地中考试卷，我们可以发现不少以二次函数知识为背景的压轴题.因其可以涵盖初中数学的许多知识点，具有较强的综合性，所以广受各地中考命题人员的青睐.掌握二次函数综合性问题，要求我们做习题后，要注重对同类型的问题进行一般性的总结，得出实用的规律，帮助我们简化解题，有些难点就能较快突破.下面就一类由二次函数图像上的点生成的问题来探求其中的方法与规律.

一、问题生成类型

问题：抛物线y=-x2-2x+3的图像交x轴于A、C，交y轴于点B，点D是抛物线的顶点，作抛物线的对称轴，连接BC.你能求出图1中A，B，C，D各点的坐标吗？根据以上信息，能设计怎样的问题来考呢？

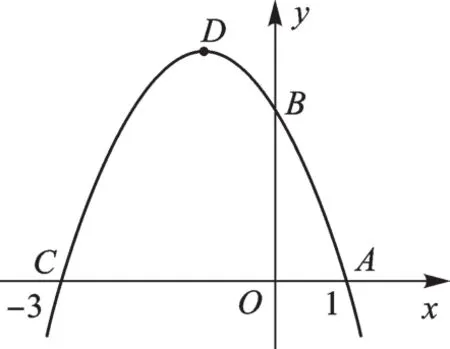
图1

【评析】抛物线上的点形成的几何图形通常会从以下几个方面设计考点：线段长度，线段最值问题，线段位置关系，与图形面积有关的最值问题，三角形的形状，形成三角形相似，特殊角等.

二、问题应用举例

生成问题1：抛物线y=-x2-2x+3在x轴上取一动点P（m，0），-3＜m＜-1过点P作x轴的垂线，分别交抛物线、CD、CB于点Q、F、E，根据以上条件，用m来表示图2中点Q、F、E的坐标，线段QF、EQ、FE的长度.

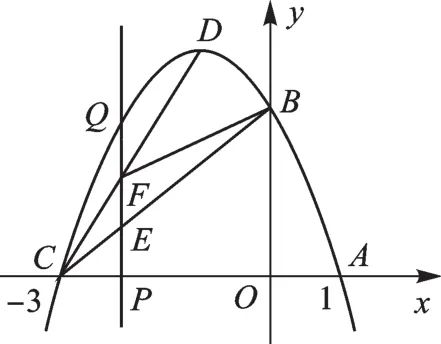
图2

【解析】本题分别求出过C、D与过C、B两点的两直线解析式：yCD=2x+6、yBC=x+3，把x=m分别代入各个解析式可得各点坐标：Q（m，-m2-2m+3），F（m，2m+6），E（m，m+3），各线段长可表示为：

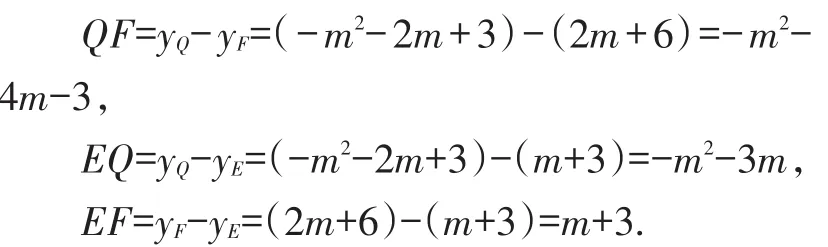
【评析】坐标系中垂直于x轴上点的坐标基本性质：直线上点的横坐标相同，直线上两点间距离等于纵坐标之差.

生成问题2：在运动过程中，是否会存在QF=EF的情况，若存在，求出m的值；如不存在，说明理由.

【解析】由问题1中求得的线段QF=-m2-4m-3，EF=m+3建立方程-m2-4m-3=m+3，可求得m的值：m1=-2，m2=-3（舍去）.

生成问题3：当m为何值时，BF与x轴平行？

【解析】根据图形中隐含条件PF∥OB，所以当BF与x轴平行时，四边形POBF是矩形，此时PF=OB=3，由PF=yF=2m+6=3建立方程，解得m=-.

生成问题4：判断线段EF与EP的长度关系，并说明理由.

【解析】EF=EP.

理由：根据问题1中F（m，2m+6），E（m，m+3）可求出EP=yE=m+3，EF=（2m+6）-（m+3）=m+3.∴EP=EF.

【总结】解决以上4个问题都应用了坐标系中垂直于x轴的直线上点坐标的性质.所以在解决函数图像上的点生成的问题中，多归纳基本图形的特性，解题往往能一击制胜.下面继续挖掘该图形生成的系列问题.

生成问题5：如图3，连接QC，QD，当m为何值时，△CDQ的面积最大？

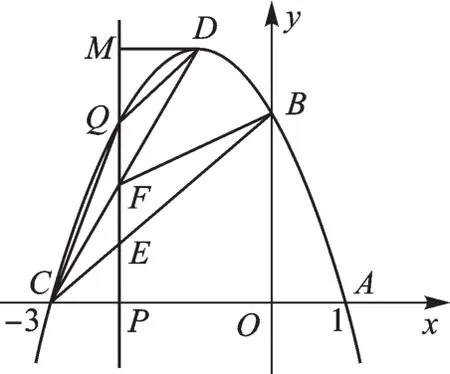
图3

【解析】由问题1中求得的线段QF=-m2-4m-3，△CDQ的面积借助直线QF分割为两部分：△CQF和△DQF，则S△CDQ=S△CQF+S△DQF

【评析】解决二次函数图像中斜三角形面积问题，通常采用割补法将复杂、不规则的面积图形分割成若干个三角形计算.分割时要注意以下几点：①分割后的三角形面积应该容易计算；②一般的分割方法为横向或纵向；③如有必要，也可斜向分割.如本题中也可连接DP，应用补的方法，先计算四边形DQCP的面积，再减去△DCP的面积.有时可能要进行多次尝试，才能找到更为简单的计算三角形面积的方法.二次函数图像中的斜三角形面积最值问题，是近几年各地数学中考试卷中很常见的题型，并且大部分题目是作为压轴题出现的.

生成问题6：当m为何值时，△BEF为等腰三角形？

【解析】由问题1中的求得点坐标F（m，2m+6）、E（m，m+3），由点B（0，3）可表示出线段EF，BF，BE的长，分别利用EF=BF，EF=BE，BF=BE建立方程使问题得解.

生成问题7：当m为何值时，△BEF为直角三角形？

【解析】仿照问题6，由点坐标表示出△BEF三边EF，BF，BE的长.该问题中因为-3＜m＜-1可得∠BEF和∠EBF均是锐角，所以使△BEF为直角三角形的只有∠BFE=90°一种情况.由勾股定理建立方程可求得m值，或由∠BFE=90°时四边形POBF为矩形可得PF=OB，即2m+6=3，建立方程可解得m的值.

【评析】解决等腰三角形、直角三角形等有关问题时要注意分类讨论，不要造成漏解.由抛物线上的点形成的几何图形可以生成许多问题.如本题还可生成问题：当m为何值时△CEF与△CFB相似.

我们能在做习题的基础上多总结一些方法，发现一些规律，识别基本图形，关注基本图形的特性，在解压轴题的过程中，能恰当地运用基本图形的性质，这些难点就能迎刃而解.

（作者单位：江苏省宿迁市宿豫区实验初级中学）