整理易错环节增强学习信心

李先永

整理易错环节增强学习信心

李先永

二次函数是初中数学的重要内容，它内容丰富，题型多变.在学习过程中，很多同学都感到“每天都花很长时间去学习，结果成绩却不尽如人意”，并为之深深苦恼.其实掌握必要的基础知识，结合函数图像进行思考，再加上细心谨慎地审题，二次函数并不难.本文结合同学们平时作业与练习中的易错点进行分析，并给出一些解决的对策和学习建议，希望同学们能树立起学好二次函数的信心.

预警一注意二次项系数a≠0

例1二次函数y=（m-3）x2+20x+m2-m-6的图像过原点，则m=.

【错解】易得m2-m-6=0，解得m=3或m=-2.

【正解】答案应注意m-3≠0，将m=3舍去，从而m=-2.

预警二注意b2-4ac≥0

例2已知抛物线y=x2-（k-1）x-3k-2与x轴交于点A（α，0），B（β，0），且α2+β2=17，求k的值.

【错解】∵抛物线y=x2-（k-1）x-3k-2与x轴交于A（α，0），B（β，0）两点，

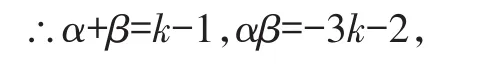
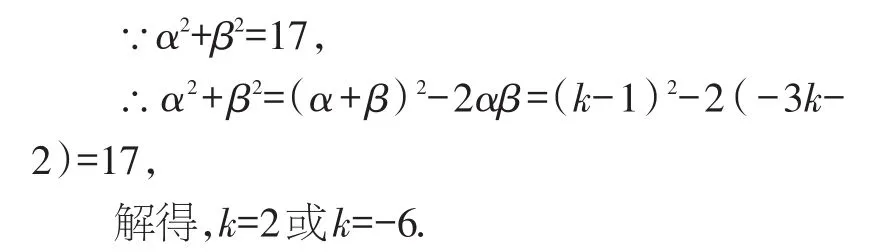
【正解】由题意知方程x2-（k-1）x-3k-2=0的两根为α，β，

由韦达定理得：α+β=k-1，α·β=-3k-2，

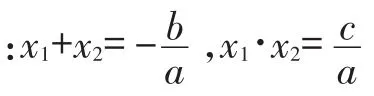
【点评】一元二次方程ax2+bx+c=0（a≠0）根与系数的关系，该关系是在判别式b2-4ac≥0的前提下得到的，因此本题在求得k值后，必须判断k是否能够使得b2-4ac≥0.

预警三注意讨论函数类型

例3若函数y=（a-1）x2-4x+2a的图像与x轴有且只有一个交点，求a的值.

【错解】∵函数y=（a-1）x2-4x+2a的图像与x轴有且只有一个交点，

Third is viability,since Zhuang drama emerge in the folk,most of its contents were transmitted from generation to generation through folk artists’oral teaching and demonstration.

∴b2-4ac=16-4（a-1）×2a=0，

解得：a1=-1，a2=2.

【正解】∵函数y=（a-1）x2-4x+2a的图像与x轴有且只有一个交点，

当函数为二次函数时，b2-4ac=16-4（a-1）×2a=0，

解得：a1=-1，a2=2，

当函数为一次函数时，a-1=0，解得：a=1.

故答案为：-1或2或1.

【点评】当题干未明确指出函数是否为二次函数时，应对字母的取值范围进行讨论.在解题过程中，容易主观地认为函数y=ax2+bx+c为二次函数，而忽略函数为一次函数的情况.

预警四注意自变量的取值范围

【错解】当x=0时，y=-2；当x=3时，y=1.所以当0≤x≤3时，y最小值为-2，y最大值为1.

【正解】y=x2-2x-2=（x-1）2-3，所以对称轴是直线x=1，顶点坐标是（1，-3），画出大致图像，如图1中抛物线位于0≤x≤3的一段，显然图像上最高点是点A，最低点是顶点而不是端点B，所以当0≤x≤3时，y最小值为-3，y最大值为1.

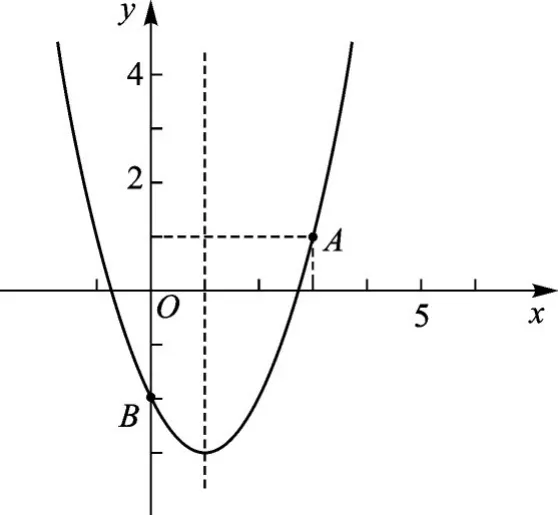
图1

【点评】解答本题时同学们经常会错误地认为端点的值就是这段函数的最值，而忽略了顶点是否在这部分函数图像上.事实上，这道题除了考查二次函数的增减性和最值以外，还考查了数形结合思想，正确解决它只要画一画图像就可以办到了.

例5某批发商以40元/千克的价格购入了某种水果500千克.据市场预测，该种水果的售价y（元/千克）与保存时间x（天）的函数关系为y=60+2x，但保存这批水果平均每天将损耗10千克，且最多能保存8天；另外，批发商保存该批水果每天还需40元的费用.

（1）设批发商将这批水果保存x天后一次性卖出，试求批发商所获得的总利润w（元）与保存时间x（天）之间的函数关系式；

（2）求批发商经营这批水果所能获得的最大利润.

【错解】（1）由题意得：w=（60+2x）（500-10x）-40x-500×40=-20x2+360x+10000；

（2）w=-20x2+360x+10000=-20（x-9）2+11620，

∴当x=9时，w有最大值11620.

【正解】（1）由题意得：w=（60+2x）（500-10x）-40x-500×40=-20x2+360x+10000；

（2）w=-20x2+360x+10000=-20（x-9）2+11620.

∵0≤x≤8，x为整数，当x≤9时，w随x的增大而增大，

∴x=8时，w取最大值，w最大=11600.

答：批发商所获利润w的最大值为11600元.

【点评】解答本题时同学们经常只关注到函数解析式本身，而忽略了实际问题中的自变量往往受到实际情况的制约，即自变量是有取值范围的.此题中的“最多能保存8天”，即0≤x≤8，x不能取9，故根据函数增减性知当x=8时，w有最大值11600.

从以上几个例题可以看出，在解答二次函数问题时，同学们要认真审题，详细分析，周密思考，慎重求解，同时要注意挖掘隐含条件.

（作者单位：江苏省宿迁市宿豫区实验初级中学）