双对数利率期限结构模型及其实证研究
张清洁
(安徽财经大学 金融学院,安徽 蚌埠 233030)
双对数利率期限结构模型及其实证研究
张清洁
(安徽财经大学 金融学院,安徽 蚌埠 233030)
近年来,随着中国利率市场化的快速发展,利率研究的现实意义变得越来越重要。利率期限结构模型的研究对于利率的确定和应用具有非常重要的现实意义。首先利用短期利率对双对数利率期限结构模型进行参数估计,然后选取5只在上海证券交易所交易的国债,并用马尔可夫链蒙特卡洛法对选取的国债进行价格模拟,分析真实价格与模拟价格的误差率。
双对数利率期限结构模型;债券定价;马尔科夫链蒙特卡罗法
利率作为资金的价格,反映了资金的供给和需求,并受到一系列宏观因素的影响,如价格水平和经济周期等。短期无风险利率作为金融市场上一个非常重要的经济变量,它与人们的社会经济活动有着密切的联系。莫顿(Merton) 最先把随机过程引入到利率的期限结构模型中。由于莫顿模型的漂移函数是常数,因此很难描述利率均值回归的特点,同时该模型并不能排除利率为负值的可能性[1]。近年来,随着中国货币市场的快速发展,对中国利率期限结构模型的实证分析显著增加。吕兆友(2004)分别采用广义矩估计方法、极大似然估计方法和有效矩估计方法对CKLS模型进行了参数估计,并对嵌套模型进行了比较分析[2]。刘金全(2006)引入区制转换对利率期限结构的非线性特征进行实证研究。得出该模型优于原模型的结论[3]。范龙振(2004)研究了多因子瓦西塞克模型,发现多因子利率期限结构模型能提高收益曲线的拟合精度[4]。高驰(2006)采用滤波法和极大似然估计法研究了三因子利率期限结构模型[5]。张蕊(2009)在利率期限结构模型中引入了四因子,并对其流动性溢酬进行了实证分析[6]。李雪(2015)利用Vasicek模型对我国同业拆借市场进行静态研究,得出市场利率波动性较为平稳的结论[7]。赵晶,张洋,丁志国(2015)通过采用六个利率期限结构模型,分别基于2008年7月至2014年3月中国和美国市场的月度国债收益率数据进行拟合与预测,并采用均方误差(RMSE)和平均绝对误差(MAE)对实证效果进行判别[8]。黄德权(2016)采用上海证券交易所日国债数据,选择Nelson-Siegel模型对收益率曲线进行拟合[9]。鲁波(2016)采用HMM模型和NS模型对中国银行间国债利率期限结构进行了实证研究[10]。沈根祥,陈映洲(2015)对动态Nelson-Siegel模型进行扩展,引入第二个斜率因子[11]。
1 双对数利率期限结构模型的提出及其参数估计
单因子利率模型中的瞬时利率过程一般形式为:
drt=μ(rt)dt+σ(rt)dWt
式中,σ(rt)dWt为利率期限结构的扩散函数,μ(rt)dt为利率期限结构的漂移函数,瞬时利率会随着这两个函数的变动而变动,其中Wt为随机利率波动项。从瞬时利率的公式可以看出,对其有影响的因素都是当前的数据,和影响因素的历史数据没有关系。由此可见,单因子利率期限结构中的瞬时利率具有马尔科夫性。
通过对国内外学者的研究进行梳理和总结之后发现,国内外学者普遍认为单因子利率期限结构模型的漂移函数应该表现为非线性的特征,因此本文提出了一种漂移函数和扩散函数都包含对数的利率期限结构模型:
dr=(a0+a1lnr)dt+σlnrdw
因为在现实生活中利率一般不会为负值,所以以往的利率期限结构并没有克服这个缺点。本文提出的双对数利率期限结构模型能很好地克服这一缺陷,保证了利率的取值为正。
1.1数据选取
在国内的货币市场利率中,相对于其他利率来讲,银行间国债市场的7天回购利率R007对瞬时利率rt的替代度比较高。潘冠中(2004)使用IBO 007是同业拆借市场的最佳利率选择,但是相对于银行间债券,选择R007作为估计数据是较好的选择。
本文选择2006年1月4日至2014年12月31日上海证券交易所债券市场的R007为数据基础。为了对单因子利率期限结构模型的漂移函数的非线性进行检验,本文通过分析R007及其一阶差分的散点图进行验证。首先对R007序列求一阶差分DR007,并绘制出R007与DR007的散点图。图1的横坐标代表R007,纵坐标代表DR007,由该散点图不仅可以看出R007与DR007呈现出明显的非线性特征,而且还可以看出,R007与DR007之间表现出了异方差的特性,即DR007随着R007由小到大的变化表现出由集中到分散的特点。因此,由图1可以初步判断漂移项是短期利率水平的非线性函数。

图1 2006.1.4—2014.12.31一阶差分DR007—利率R007散点图
1.2数据的描述统计
对本文使用的2006年1月4日至2014年12月31日的原始数据进行描述性统计分析,得出其走势图如图2所示。

图2 2006.1.4—2014.12.31的R007 走势图
本文在表1中对R007的一些比较重要的描述性统计数据进行了汇总。对表1中的结果进行分析可以得出, R007序列具有非正态性。

表1 2006.1.4—2014.12.31 R007的统计特征
1.3数据的平稳性分析
对样本期内R007进行ADF检验,得出银行间七天回购利率的T值为-7.177053,在一定的显著性水平下,银行间七天回购利率的T值小于临界点,拒绝了原假定,即R007利率时间序列没有单位根,所以R007利率时间数列是平稳序列。因此,R007具有均值回复性,可以代表短期瞬时利率对利率期限结构模型进行实证检验。
1.4参数估计
因为双对数利率期限结构模型是一种连续微分方程,而本文的R007数据是离散的交易数据。因此,为了估计双对数利率模型的参数,必须先对该模型实施离散化。所以,利率期限结构模型的离散化是参数估计的关键,本文采用Euler离散法进行离散化处理。
由于本文提出的双对数利率期限结构模型无法求解黎卡提微分方程,使用马尔科夫链蒙特卡洛法对双对数利率期限结构模型进行参数估计,应该先对待估参数设置先验分布,本文设置的待估参数的先验分布为:a0~N(0,0.01),a1~N(0,0.01),a2~N(0,0.01),itau~Gamma(2.5,0.025),其中itau=1/σ2。
(1) 参数的估计结果
本文使用马尔科夫链蒙特卡洛估计法对双对数利率期限结构模型进行参数估计,使用的估计软件是OPENBUGS。为了克服由于初始值设定的影响,需要进行“退火”处理 。“退火”处理后,只引用最后30001次迭代的结果,我们可以得到a0、a1和itau的参数估计。

表2 利用R007估计的MCMC结果


(2)收敛性检验
只有在马尔可夫链蒙特卡洛估计法得出的参数估计结果收敛时,才能说明估计结果是可用的。因此,有必要对参数进行收敛性检验。本文可以通过观测核密度图的光滑度来判断该模型参数的敛散性,双对数利率期限结构模型的核密度如图3所示。
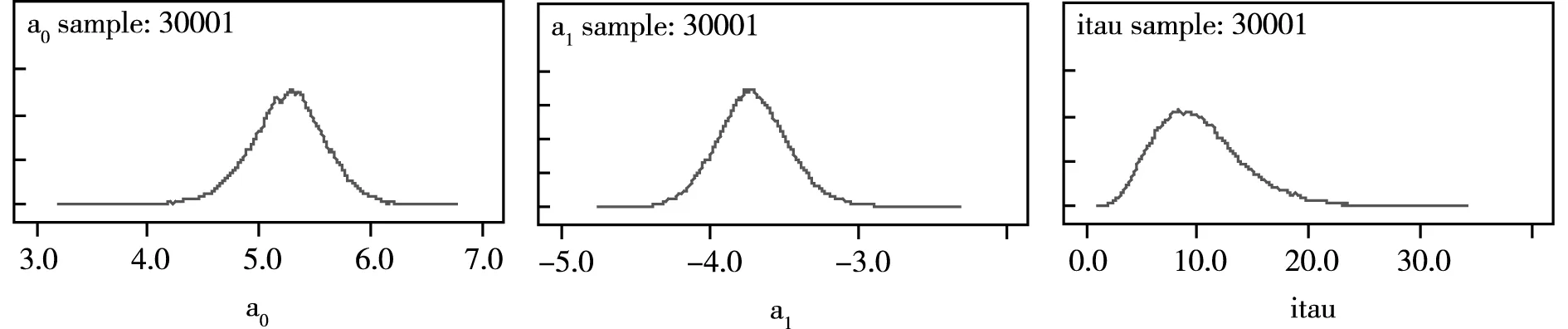
图3 a0、a1和itau的核密度图
从3个参数的核密度模拟结果可以看出,除了一些不规则的部分,核密度曲线的整体还是相对光滑的,这说明利用马尔可夫链蒙特卡洛法估计出的参数都是收敛的。各参数的迭代轨迹如图4所示。



图4 利用R007估计的双对数利率期限结构模型参数的迭代路径
由图4可以看出,在进行“退火”处理之后的估计结果的迭代路径的变动比较稳定 ,因此,本文认为利用R007对双对数利率期限结构模型进行的参数估计有效收敛。
2 国债定价
只有将利率期限结构模型真正地应用在现实的经济活动中才能真正体现它的研究价值。而现实生活中利率期限结构模型的一个重要用途就是国债定价。
2.1蒙特卡罗模拟定价原理
国债的定价法有很多种,不同国债定价法的原理不一样,使用最广泛的方法是先对利率模型进行参数估计,在得出利率期限结构模型就可以得出债券的价格。该方法需要用到风险的市场价格,而且粉线的市场价格主要通过认为的预先设定,因此,市场风险价格的设定就存在很大的主观性。为了减少市场风险价格等主观因素的影响,本文采用了蒙特卡罗模拟方法对国债进行模拟定价。
蒙特卡罗模拟定价法分为四个步骤。
第一、利用估计出的双对数利率期限结构模型,对利率路径进行模拟。
第三、由公式D(t)=E[Dj(t)]得出折现系数的数学期望。
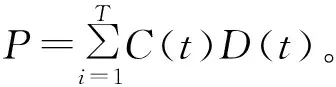
2.2国债定价
本文选取了上海证券交易所2014年12月31日买卖的5只债券进行价格模拟。由前面的模型参数估计得到的利率期限模型为:

首先利用MATLAB软件求出每个债券各期的折现系数,然后根据得出的各期贴现系数和各期现金流量就可以得出国债的价格。定价结果如表3所示。

表3 模拟出的国债价格
由表3可以看出,利用双对数利率期限结构模型对国债进行价格模拟的模拟结果与其真实价格的差异还是比较小的,说明双对数利率期限结构模型对国债价格的模拟还是比较理想的。从表3模型的定价结果我们还可以看出,剩余交易期限短的债券模拟出的价格误差相对于剩余交易期限长的债券模拟出的价格差较小。本文认为得出以上结果的原因主要有: (1)我国国债市场处于分割的状态。 (2)模型设定的偏误。
2.3误差修正模型
由以上部分的研究分析可以看出,双对数利率期限结构模型的国债定价效果并不理想,因此,为了让该模型的定价更加精确,本文将对其进行误差修正。以误差EP为纵坐标,剩余交易期限T
为横坐标,如图5所示。

图5 定价误差与剩余期限的散点图
由图5可以看出,误差修正函数应该具有二次函数的特征,所以,把误差修正模型设定为:
EP=α+βT+γT2+ε
利用OLS对参数进行估计,结果如表4所示。

表4 误差系数估计结果
因此,得到的误差修正函数为:
EP=-7.07+0.0147T-(3.4E-06)T2+ε
由误差修正模型对国债定价进行误差修正,结果如表5所示。

表5 模拟的国债价格
将修正后的定价结果和修正前的定价结果进行对比可以发现,修正后的定价结果与实际价格非常接近,说明修正后的国债定价效果有了非常显著的提高。综合来说,误差修正模型对国债定价准确性的提高有着显著意义。
3 结论
本文首先利用银行间七天回购利率(R007)序列及其差分序列绘制出散点图,得出漂移项是短期利率水平的非线性函数的结论,进而引入一种漂移函数及扩散函数均包含利率对数的双对数利率期限结构模型。然后选取银行间债券七天回购利率,利用马尔科夫链蒙特卡罗估计方法(MCMC)对双对数利率期限结构模型进行参数估计,并对估计所得到的结果进行分析。最后利用马尔可夫链蒙特卡洛国债定价法对上海证券交易所的5只国债进行模拟定价。本文的结论如下。
(1)单因子利率模型的漂移项是一个非线性的函数。
(2)中国的银行间债券回购市场的利率存在均值回归的现象。
(3)利用马尔可夫链蒙特卡洛法对国债定价的结果表明,双对数利率期限结构模型能够较好地估计出债券的价格。且剩余交易期限短的债券模拟出的价格误差相对于剩余交易期限长的债券模拟出的价格差较小。
[1]Merton, R. Theory of Rational Option Pricing[J].Bell Journal of Economics and Management Science, 1973(4): 141-183.
[2]吕兆友.中国银行间债券市场国债回购利率随机行为的实证研究[J].管理科学,2004(12):62-66.
[3]刘金全,郑挺国.利率期限结构的马尔科夫区制转移模型与实证分析[J].经济研究,2006(11):82-91.
[4]范龙振.以1年期储蓄存款利率为状态变量的跳跃型广义Vasicek模型[J].管理科学学报,2010(10):69-78.
[5]高驰,王擎.我国利率期限结构动态研究——基于卡尔曼滤波的仿射模型实证[J].南方经济,2006(12):19-26.
[6]张蕊,王春峰,房振明,梁崴.上交所国债市场流动性溢价研究——基于4 因子仿射利率期限结构模型[J].系统管理学报,2009(10):481-486.
[7]李雪.基于Vasicek模型的我国同业拆借利率期限结构静态研究[J].中央财经大学,2015 (s2) :3-9.
[8]赵晶,张洋,丁志国.利率期限结构特征的拟合与预测[J].统计研究,2015(2):83-89.
[9]黄德权,苏国强基于Nelson—Siegel模型的中国利率期限结构实证研究[J].金融理论与实践,2016(5):12-17.
[10]鲁波.中国银行间国债利率期限结构实证研究[J].浙江财经大学,2016.
[11]沈根祥,陈映洲. 双斜率因子动态Nelson-Siegel利率期限结构模型及其应用[J].中国管理科学,2015(10)1-10.
ClassNo.:F832.1DocumentMark:A
(责任编辑:蔡雪岚)
EmpiricalStudyofDoubleLogarithmicTermStructureModel
Zhang Qingjie
(School of Finance, Anhui University of Financeamp; Economics, Bengbu, Anhui 233030,China)
In recent years, with the rapid development of China's interest rate market, the practical significance of interest rate research becomes more and more important. The research on term structure model of interest rate is very important for the determination and application of interest rate. This paper first use short-term interest rates as parameters of the double logarithmic model of interest rate term structure estimation, then select 5 in the Shanghai stock exchange bonds, and selection of the Treasury bond price simulation with Monte Carlo method, compared with its real price. In this paper the double logarithmic model of interest rate term structure is more reasonable and accurate to estimate the term structure of interest rate of bond market in our country, and then improve the validity of interest rate risk management, the accuracy of financial product pricing and macroeconomic forecast.
double logarithmic term structure model; bond pricing; Markov Monte Carlo
张清洁,硕士,安徽财经大学。
2096-3874(2017)11-0091-06
F832.1
A

