数字图像处理课程教学中成像逆问题的正则化处理方法初探

肖 宿

(淮北师范大学 计算机科学与技术学院，安徽 淮北 235000)

数字图像处理课程教学中成像逆问题的正则化处理方法初探

肖 宿

(淮北师范大学 计算机科学与技术学院，安徽 淮北 235000)

成像逆问题是数字图像处理课程的重要内容，该问题的研究近年来获得了快速发展，但现有教材中成像逆问题的内容多局限于基本理论、基本方法，涉及其最新研究进展的不多，内容讲授存在一定的“照本宣科”现象。针对此，试介绍成像逆问题基本内容、建模表示及研究进展，然后对成像逆问题当前常见的正则化处理方法进行初步探讨，最后通过实验展示某些方法的处理效果，以有助于数字图像处理课程教学活动的开展，帮助学生深入理解成像逆问题等内容。

数字图像处理；成像逆问题；教学研究；正则化方法

引言

数字图像处理是许多高校计算机及相关专业开设的一门基础课程，它主要讲述数字图像处理相关的理论、方法、技术和应用，内容涵盖了图像变换、图像滤波、图像压缩、图像分割、图像表示与建模、图像复原、图像识别等，要求学生能够掌握数字图像处理的基本方法并通过编程实现。作为一门新兴的学科，其课程开设的历史并不长，国内高校从上个世纪80年代才陆续开设数字图像处理课程。但早在上个世纪20年代国内外学者就已开展了相关研究[1]，上个世纪60年代数字图像处理形成一门学科。随着数字图像处理技术的发展和应用的深入，成像逆问题作为其中重要的基础性问题越来越受到重视。成像逆问题主要包括图像去模糊、图像去噪和图像修复等内容[2]。近几十年来，成像逆问题研究的发展极其迅速，许多新理论、新算法、新技术层出不穷[3-5]，而高校数字图像处理课程教材中涉及的内容总体相对滞后、不全面，无法准确反映成像逆问题的研究现状。又因成像逆问题需要一定的数学背景知识，其内容较复杂、较难理解，在讲授数字图像处理课时，成像逆问题相关内容已被忽略或出现“浅尝辄止”不做深入剖析的情况。针对目前成像逆问题的授课现状及存在的问题，本文将全面介绍成像逆问题及其研究状况，初步探讨该问题流行的处理方法，在实验部分还将对某些方法的处理效果进行展示。

一、成像逆问题

受光线、天气、摄影技术和成像设备性能等因素的综合影响，质量退化是图像中一个比较普遍的现象。图像质量退化形式主要有图像模糊、图像含噪和图像像素丢失等，退化过程可统一表示为：

y=Hx+n

(1)

式中，y∈Rn表示已知退化图像向量形式；H∈Rm×n表示矩阵形式的线性算子，常见如模糊算子、单位矩阵等；x∈Rm是未知清晰图像的向量形式，n∈Rn表示加性噪声。对于有重大价值的图像而言，比如1964年美国探索火星计划耗资千万美元得到的22幅图像，如果产生质量退化无疑会造成巨大损失。即使是普通的图像，发生质量退化仍是人们不愿意看到的。因此，国内外研究者很早就开始探索能够“逆转”图像质量退化的技术和方法，以复原出清晰的图像，即所谓的“成像逆问题”。尤其在当今的数字图像时代，成像逆问题的研究和探索更具有应用价值和现实意义。处理成像逆问题的难点在于它具有很强的不适定性，多年来的研究表明：正则化技术是解决不适定问题最有效的工具之一。

Tikhonov正则化[6]是早期流行的一种正则化技术，在其框架下成像逆问题被表示为：

(2)

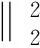
(3)

(4)

式中，B=HD；L1范数在此起到了稀疏诱导(inducing)的作用。

式(3)和(4)是目前最流行的成像逆问题表示模型，其求解方法是近年来图像处理领域研究的热点之一。

二、成像逆问题(3)和(4)的解法

成像逆问题问题(3)和(4)的传统求解方法主要有内点法(interior point)[10]、梯度投影方法(gradient projection)[11]、LASSO方法[12]等。为追求更快、更精确处理成像逆问题，近年来一些新方法被提出，其中最著名的、最具代表性的是快速迭代收缩阈值法(FISTA)[13]和交替方向乘子法(ADMM)[2]。

FISTA由A. Beck等人提出，作为Nesterov优化梯度方法[14]的变体，它以如下方法分别处理成像逆问题(3)和(4)：

ADMM最早由R. Glowinski等人[15]提出，M. Afonso等人将其用于处理式(3)和(4)中的成像逆问题，其处理方法分别如下：

其中，步骤6所示最小化问题的解为著名的软阈值函数(soft-thresholding)[16]。

三、仿真实验

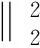
(a)

(b) (c)图1 清晰图像和质量退化图像(a) 清晰图像；(b) 模糊图像； (c) 损坏图像

(a) (b)

(c) (d)图2 模糊图像复原结果(a) FISTA-TV获得的结果 (ISNR=8.58dB)； (b) FISTA-L1获得的结果 (ISNR=7.73dB)； (c) ADMM-TV获得的结果 (ISNR=7.97dB)； (d) ADMM-L1获得的结果 (ISNR=7.70dB)

(a) (b)图3 损坏图像复原结果(a) FISTA-TV获得的结果 (ISNR=18.90db)； (b) ADMM-TV获得的结果 (ISNR=18.60dB)

结论

本文研究了数字图像处理课程中一类重要问题——成像逆问题，对该类问题当前最流行的解法进行了初步探讨，通过实验展示了FISTA和ADMM两种方法的复原效果。针对目前数字图像处理课程在成像逆问题方面的内容不够全面、不够新颖，本文研究的内容可作为日常教学的一个参考和补充，通过本文对相关内容的介绍和讨论可加深学生对成像逆问题的理解，激发其进行更深入探讨的兴趣。

[1]阮秋琦. 数字图像处理学 [M]. 第3版. 北京: 电子工业出版社, 2013.

[2]Afonso M V, Bioucas-Dias J M, Figueiredo M A T. Fast image recovery using variable splitting and constrained optimization[J]. IEEE Transactions on Image Processing, 2010, 19(9): 2345-2356.

[3]Chen Y, Pock T. Trainable nonlinear reaction diffusion: a flexible framework for fast and effective image restoration [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(6): 1256-1272.

[4]李博, 谢巍. 基于自适应分数阶微积分的图像去噪与增强算法 [J]. 系统工程与电子技术, 2016, 38(1): 185-192.

[5]Ruzic T, Pizurica A. Context-aware patch-based image inpainting using Markov random field modeling [J]. IEEE Transactions on Image Processing, 2015, 24(1): 444-456.

[6]张路寅, 张玉海, 钱坤明. 关于不适定问题的迭代Tikhonov正则化方法[J]. 山东大学学报(理学版), 2011, 46(4): 29-33

[7]Needell D, Ward R. Stable image reconstruction using total variation minimization [J]. SIAM Journal on Imaging Sciences, 2013, 6(2): 1035-1058.

[8]Rudin L I, Osher S. Total variation based image restoration with free local constraints [J]. Proceedings of the IEEE International Conference Image Processing (ICIP), Austin, TX, USA, 1994(1): 31-35.

[9]邓承志. 图像稀疏表示理论及其应用研究 [D]. 武汉: 华中科技大学, 2008.

[10]Fu H, Ng M K, Nikolova M, Barlow J L. Efficient minimization methods of mixed l2-l1 and l1-l1 norms for image restoration [J]. SIAM Journal on scientific Computing, 2006, 27(6): 1881-1902.

[11]Yu G, Qi L, Dai Y. On nonmonotone Chambolle gradient projection algorithms for total variation image restoration [J]. Journal of Mathematical Imaging and Vision, 2009, 35(2): 143-154.

[12]Shen B, Hu W, Zhang Y, Zhang Y. Image inpainting via sparse representation [C]// Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 2009: 697-700.

[13]Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems [J]. SIAM journal on imaging sciences, 2009, 2(1): 183-202.

[14]Nesterov Y.IntroductoryLecturesonOptimization[M]. Netherlands: Kluwer Academic Publishers, 2004.

[15]Boyd S, Parikh N, Chu E, Peleato B, Eckstein J. Distributed optimization and statistical learning via the alternating direction method of multipliers [J]. Foundations and Trends in Machine Learning, 2011, 3(1):1-122.

[16]孙蕾, 谷德峰, 罗建书. 基于迭代方法的软阈值估计小波去噪 [J]. 系统工程与电子技术, 2009, 31(1): 36-39.

ClassNo.:G642:TP301DocumentMark：A

(责任编辑：宋瑞斌)

RegularizationofSolvingImagingInverseProblemsintheDigitalImageProcessing

Xiao Su

(School of Computer Science and Technology, Huaibei Normal University, Huaibei, Anhui 235000, China)

Imaging inverse problems, have been developed rapidly in recent years, are one of most important parts of digital image processing. However, in the existing textbooks the contents of imaging inverse problems are restricted in basic theory and methods, rather than recent advances. And some contents of imaging inverse problems are repeated as what the text-books say. Aiming at this, this paper first introduces the basis, the modeling and the advances of imaging inverse problems, then it preliminarily discusses the popular methods of solving imaging inverse problems, and finally the restored results of some methods are experimentally demonstrated. It is hoped that this paper is helpful to carrying out the teaching activity of imaging inverse problems and helps students deeply understand this course.

digital image processing; imaging inverse problems; teaching research; regularization approach

肖宿，博士，副教授，淮北师范大学。

安徽省自然科学基金项目(1608085QF150)。

2096-3874(2017)11-0038-04

G642：TP301

A