LSHBMRPK-means算法及其应用

罗 俊，李劲华

青岛大学 数据科学与软件工程学院，山东 青岛 266071

◎大数据与云计算◎

LSHBMRPK-means算法及其应用

罗 俊，李劲华

青岛大学 数据科学与软件工程学院，山东 青岛 266071

针对传统的k-means聚类算法在处理大数据时算法时间复杂度极高和聚类效果不佳的问题，提出了LSHBMRPK-means算法，即基于局部敏感哈希函数的MapReduce并行化的k-means聚类算法；针对推荐系统的可扩展性问题，将LSHBMRPK-means应用于基于聚类的协同过滤算法。此外，针对评分数据的稀疏性问题，使用LFM，即隐语义模型，对缺失值进行填充，进而提出了基于LFM的LSHBMRPK-means聚类算法。实验结果表明，LSHBMRPK-means聚类算法提高了聚类效率和质量，基于LFM的LSHBMRPK-means协同过滤算法具有较好的可扩展性，同时解决了因评分数据稀疏导致聚类质量不好的问题。

大数据；k-means；局部敏感哈希函数；MapReduce；推荐算法

1 引言

随着大数据时代的到来，数据的规模、种类和维度激增，同时要求处理的效率越来越高。单一机器节点的计算能力已不可能满足大数据的应用需求[1]。为了将算法应用到分布式并行计算平台，需要将其进行并行化改造。k-means聚类算法是一种基于原型的创建数据对象的单层划分聚类技术[2]。由于它简单、高效，特别是在应用于大数据时具有很好的可扩展性，因而广泛用于商务智能、基因学、信息检索、心理学和医学等领域。

海量高维数据的挖掘存在两大挑战：数据的规模问题和数据的高维度问题。k-means算法在数据集增大的同时，簇数k值也随之增大。k-means算法具有独立可拆分性，可以通过使用MapReduce编程模型[3]实现并行化改造。同时，k-means算法需要多次迭代，若数据集中的所有点都与中心点进行比较，将导致巨大的计算代价，并增加了节点间的通信开销。为减少数据量，传统的方法是采样。但是，采样的方式会导致聚类结果的准确率不高。局部敏感哈希算法[4]是一种应用于大规模高维数据的技术，它能够很快搜索到最近邻的数据。它的基本思想是：在原始数据空间中有若干数据点，将相邻的数据点进行相同的投影映射后，在投影的目标低维空间中，这些数据点以很高的概率聚集在一起。本文提出了LSHBMRPK-means算法，算法首先通过局部敏感哈希函数对数据集进行分区，选出代表点代表每个分区[5]，然后使用MapReduce并行化的k-means算法对代表点集进行聚类。LSHBMRPK-means算法具有很好的可扩展性，同时提高了聚类的效率。

推荐系统的核心思想是将用户和物品联系在一起，即帮助用户找到用户感兴趣的物品，同时将物品推荐给对它有兴趣的用户[6]。传统的推荐方法主要有基于内容的方法[7]、基于邻域的方法和混合的方法。现代的推荐方法有：上下文感知的方法、基于语义的方法、基于跨领域的方法、点到点的方法和跨语言的方法。从广义上来看，推荐技术属于数据挖掘与机器学习的范畴，一个好的推荐服务依赖于科学的推荐算法和大量的学习数据。面对大数据问题，现在的推荐算法还需要考虑是否能够处理海量高维数据，以及是否能够大规模并行化等问题。

协同过滤算法是推荐系统中经常被使用的技术，它分为：基于邻域的方法、基于模型的方法以及基于聚类的方法。基于邻域的方法又分为基于物品的方法和基于用户的方法。基于用户的方法首先找到与目标用户有共同兴趣的用户群，然后向目标用户推荐他们感兴趣的但其本身不知道的物品项；基于物品的方法通过在所有的用户历史行为中查找与目标用户兴趣度相似的其他物品，然后将它们推荐给目标用户；基于模型的方法是一种机器学习的方法，它利用目标用户的兴趣度自动对物品进行分类，然后向目标用户推荐其他可能感兴趣的物品。隐语义模型（Latent Factor Model，LFM）[8]是一种典型的基于模型的协同过滤算法，它是基于机器学习的算法，从相关理论知识发展而来。基于聚类的协同过滤算法，通过对评分数据集进行聚类，得到有相似评分的簇集。传统的基于聚类的协同过滤算法，往往由于评分数据比较稀疏，导致聚类效果较差[9]。本文提出了基于LFM的LSHBMRPK-means协同过滤算法，算法首先利用LFM的方法补全高维稀疏的评分数据集矩阵中的缺失值，从而得到一个完整的评分数据集矩阵，然后利用LSHBMRPK-means算法在没有缺失值的评分数据集上以用户为向量进行聚类，预测分析测试集上的用户的未知评分。该算法能有效解决因评分数据集的数据稀疏导致的推荐结果准确率不高的问题，此外，算法还可以进行离线计算处理，从而提高推荐系统的可扩展性，同时降低线上计算负担。

2LSHBMRPK-means算法

2.1 k-means算法及其应对海量高维数据的不足

k-means算法是一种基于原型的单层划分聚类技术。算法简单、高效，被广泛应用。它首先从所有点中按某种方式选出k个初始质心，其中k是用户期望的簇个数，然后将每个点分配到距离最近的质心，形成簇集，再重新计算质心。重复分配和更新步骤，直到k个簇的质心不发生变化，算法如算法1所示。

算法1基本的k-means聚类算法

步骤1 Initially choose k centroids to be centroids

步骤2 Repeat

步骤3 Find centroid to which point is closest

步骤4 Adjust the centroids of each cluster

步骤5 Until centroids do not change

在数列、生物学、多媒体以及推荐系统等应用领域，需要处理规模和维度都很大的数据。传统的基本k-means聚类算法在处理这些海量高维数据时遇到了困难，一方面是由于数据的稀疏性[10]，另一方面是因为高维数据的距离计算问题[11]。

Verleysen[12]提出了“维度灾难”的概念，Michael Steinbach和他的同事[13]指出“维度灾难”是对高维数据进行聚类的主要挑战。高维数据与低维数据的主要区别点在于高维数据比较稀疏[14]，以及高维空间中距离计算的不同。“高维灾难”主要体现在两个方面：在高维空间中，点间的距离相差不大，几乎任意两个点向量都成直角[15]。

海量高维数据给聚类带来了数据的规模问题和高维度问题，并给现有的数据挖掘技术带来了极大的挑战。k-means聚类算法对低维和高维数据都有很好的支持，但如果数据的规模越来越大，同时k-means算法需要进行多次迭代，数据集中的所有点都与k个质心进行比较将导致巨大的比较计算代价，尽管可以使用并行化的k-means聚类算法应对大数据的规模问题，当数据的维度很大时，每个点与中心点间的距离计算，也将产生很大的计算代价。针对大数据的高维度问题，一方面可以进行维约简从而降低数据的维度，另一方面可以通过减少聚类簇数k的规模来降低计算代价。

基于排序学习的推荐算法[16]，推高了推荐算法的性能和用户的满意度，但在处理大数据问题时遇到了困难；并行化的大规模分类数据聚类算法[17]，以及启发式流程挖掘算法[18]能够处理大数据带来的挑战，但不适用于推荐算法。

2.2 局部敏感哈希函数

局部敏感哈希算法是Piotr Indyk等[19-20]在研究依靠可用的数据量线性依赖关系寻找高维相似度模式中提出的一种新方法。它是一种基于概率的在高维空间中搜索最近邻的方法，基本思想是通过一组哈希函数将数据点进行哈希，使得在新空间中，距离比较近的数据点在原始空间中的相似度也比较高。局部敏感哈希的定义如定义1所示。

定义1一组函数集H={h:S→U}被称为对于距离度量函数D，(r1,r2,p1,p2)-敏感，若任意v,q∈S满足下面的条件：

（1）Ifv∈B(q,r1)then PrH[h(q)=h(v)]≥p1；

（2）Ifv∉B(q,r2)then PrH[h(q)=h(v)]≤p2。

为了使局部敏感哈希函数的集合有效，其参数必须满足不等式：p1＞p2和r1＜r2。

LSHBMRPK-means算法根据满足局部敏感哈希函数的条件确定最佳的哈希函数集。

2.3 LSHBMRPK-means算法的基本思想

海量高维数据面临两大挑战，分别是数据的规模问题和数据的高维度问题。当k-means处理海量高维数据时，簇数k值往往很大，k-means的迭代次数明显上升，单个数据点与中心点间的距离计算代价也很大。若共有n个数据点，k个中心点，数据的维度为d，k-means的中心点距离计算的代价为o(n×k×d)。为降低比较计算的复杂度，一方面可以降低数据的规模，另一方面可以对数据点进行降维处理。本文采用降低数据的规模的方法。传统的是采用统计方法对数据点进行采样，但采样会影响数据的质量，导致聚类的准确率不高。上一小节提到的局部敏感哈希算法在处理海量高维数据时有很好的效果，因此，将利用局部敏感哈希算法降低数据集的规模，之后，再进行聚类。进而，k-means的迭代次数和聚类簇数k值都会下降，k-means算法的总复杂度也就降低了。

另外，k-means算法对海量高维数据进行聚类时，如果每个点与中心点都进行距离计算再比较，计算量会很大。由于在局部敏感哈希算法中，原始空间中距离很近的点通过哈希函数映射出来的哈希值也是相近的，通过局部敏感哈希算法划分出来的点属于同一个分类。从而可以利用局部敏感哈希算法将距离较近的点分到一个类别中，并用一个代表点代表同一分类中的点[5]。通过局部敏感哈希算法生成代表点后，再针对这些含有代表点的数据集，使用MapReduce并行化的k-means聚类算法进行聚类，详见参考文献[21]。

本文提出的LSHBMRPK-means算法包含如下两个主要步骤：

步骤1利用局部敏感哈希函数生成代表点集。

步骤2使用MapReduce并行化的k-means算法对由局部敏感哈希函数生成的代表点集进行聚类操作。

算法流程图如图1所示。

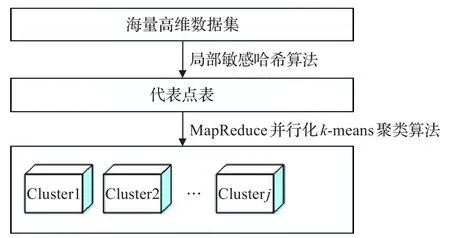
图1LSHBMRPK-means算法执行过程

2.4 LSHBMRPK-means算法描述

LSHBMRPK-means算法含有的子算法有：利用局部敏感哈希函数生成代表点集的算法和MapReduce并行化的k-means聚类算法。利用局部敏感哈希函数生成代表点集的算法如算法2所示。

算法2利用局部敏感哈希函数生成代表点集

步骤1 Select m hash functions

步骤2 Set hashArray←h1（point），h2（point），…，hm（point）

步骤3 for each hashValue of hashArray do

步骤4 Re-cluster the bucket，get a cluster and its center

步骤5Output（c1，point lists in the radius d）

步骤6 end for

算法2描述了通过局部敏感哈希算法产生出规模比较小的代表点集的方法。步骤1挑选出m个可用的局部敏感哈希函数，而且m比数据点的维度小很多。步骤2基于每个局部敏感哈希函数计算出各数据点相对于全部的哈希函数的哈希值，这些哈希值是全部数据点通过局部敏感哈希函数进行降维后得到的点。由于降维后，很多距离比较近的原始点降维后哈希值是相近的，所以，步骤3至步骤6中对每个由相同哈希值组成的桶（数据集）进行聚类。具有相同哈希值组的点聚集在一起，代表点的半径用参数d表示。由于具有相同哈希值组的点距离也都比较近，也还有很少的点可能距离不是很近，因而使用k-means聚类算法对这些点进行聚类，聚类的簇数为1，从而产生代表点代表由相同哈希值组成的桶。进而，得到一个降低规模的代表点集，此代表点集是通过对原始数据集进行局部敏感哈希操作得来的，它能够有效代表原始数据集。然后使用MapReduce编程模型对基本的k-means聚类算法进行并行化改造，使其能够处理大数据问题，且算法将具有较好的可扩展性。然后，针对规模较小的数据集使用MapReduce并行化的k-means聚类算法，所需时间比在原数据集上执行MapReduce并行化的k-means算法要少，同时随着集群规模的增大，在一定范围内，算法的执行效率也逐渐提高。另外，通过选取代表点的方式能够防止彼此距离比较近的两个点同时被当作初始中心点的问题。同时，由于数据规模的减少以及k-means的质心更新次数的降低，能有效降低集群的网络开销。

3 基于LFM的LSHBMRPK-means协同过滤算法

本文将LSHBMRPK-means算法应用到基于聚类的协同过滤算法中，同时利用LFM补全稀疏的评分数据集，提出了基于LFM的LSHBMRPK-means协同过滤算法，算法的具体算法步骤如下：

步骤1利用评分数据集，生成用户-项目评分矩阵。由于数据量很大，很多评分数据是缺失的，因而得到的用户-项目评分矩阵是比较稀疏的。

步骤2使用LFM填充稀疏的评分矩阵。利用用户的历史评分数据中提供训练用的用户-项目评分数据集，计算用户u会给物品i打几分。在填补完所有训练用户的缺失评分后，得到一个完整的用户-项目评分矩阵 R′。

步骤3使用LSHBMRPK-means算法聚类分析完整的用户-项目评分数据集R′。采用LSHBMRPK-means算法以用户为向量对评分矩阵进行聚类分析，通过聚类，获得相近的用户类别：U1,U2,…,Uj，通过多次实验结果获得聚类类别的最优个数 j。

步骤4预测用户评分。一个用户a使用推荐系统时，通过分析该测试用户的历史评分数据来计算用户a与每个聚类类别中心的距离，随后把用户分配到相应的聚类类别Um(m∈[1,j])中去。

通过搜索测试用户的聚类类别Um来计算与它相似的其他用户。这种方式，不仅使推荐系统算法具备了可扩展性，同时也极大地提高了计算效率。

用户a与b之间的相似度Sim(a,b)用公式（1）表示。

通过在目标用户a所在的聚类簇Um中查找它的最近邻集合来预测用户评分，提高算法的执行效率和可扩展性。然后使用公式（2）计算用户的未知评分项。

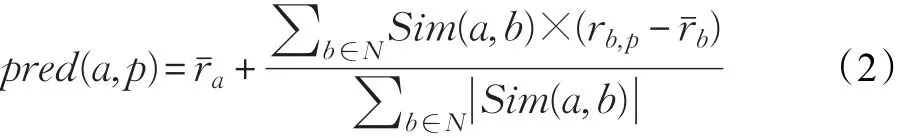
本算法的流程图如图2所示。

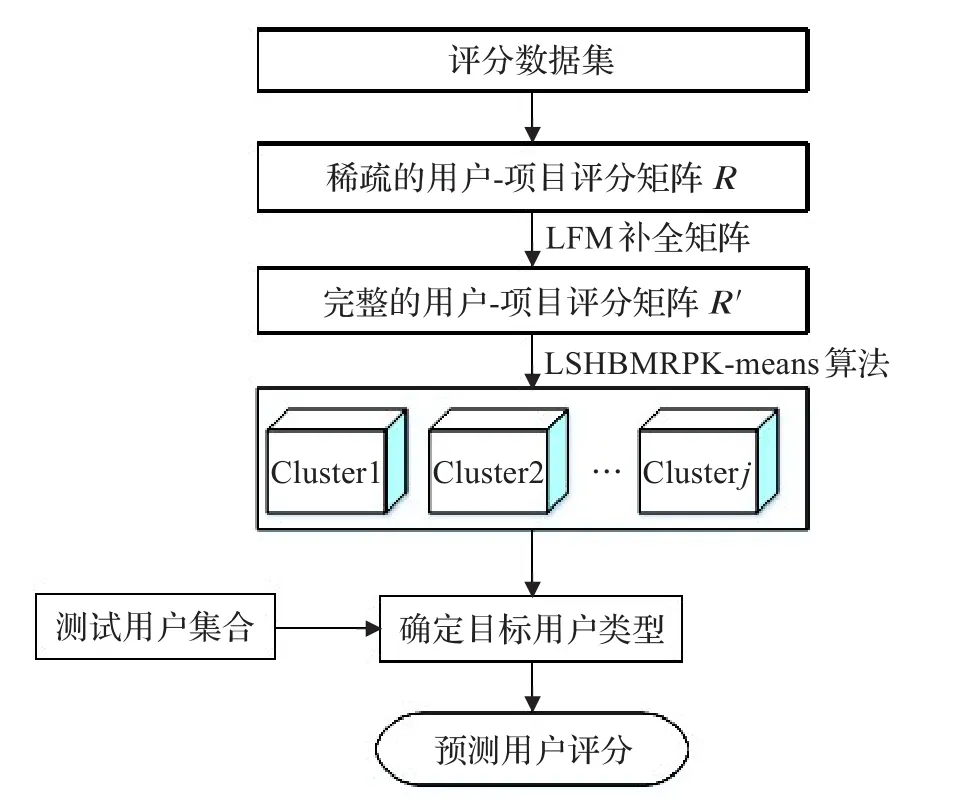
图2 基于LFM的LSHBMRPK-means协同过滤算法流程图

4 实验设计与结果分析

4.1 实验环境与实验数据集

实验环境中Hadoop集群共有三个节点，有一个主节点，两个从节点。

实验集群是由搭建在ESXI 5.5上的三台Linux虚拟机组成，各节点所使用的Hadoop版本均为2.7.1。各节点的配置信息均为，CPU：10个2.13 GHz主频的单元，内存：40 GB，磁盘：300 GB。

本文采用GroupLens小组提供的MovieLens数据集（http：//grouplens.org/datasets/movielens/20m/.）对推荐算法进行测评。实验选用的数据集包含了138 493个用户对27 278部电影的评分数据，总的评分数据达20 000 263条。该数据集是公开的，具有较高的可靠性。评分等级由0.5～5.0，增量是0.5，表示用户对电影的喜欢程度越来越高。

数据集由4个文件组成：links.csv、movies.csv、ratings.csv和tags.csv。所有的评分数据都在ratings.csv文件中，文件格式为：userId、movieId、ratings、timestamp。Movies.csv收集了movieId、title和genres信息。

4.2 实验设计

实验内容包括：LSHBMRPK-means算法和基于LFM的LSHBMRPK-means协同过滤算法。针对LSHBMRPK-means算法，选择的评价指标为聚类簇的个数、算法执行时间和局部敏感哈希函数的有效性；针对基于LFM的LSHBMRPK-means协同过滤算法，选择的评估指标有：聚类的簇数与推荐性能的关系。推荐系统的离线实验只需收集用户的历史评分数据，不需要搭建系统，也无需用户参与。离线实验可以很方便地对很多推荐算法进行测试。本实验步骤设计如下：

步骤1将所有的评分数据随机均匀的分成M(M=10)份，取其中一份作测试数据集，M-1份训练数据。

步骤2用训练数据集生成稀疏的用户-项目评分矩阵。

步骤3使用LFM补全用户-项目评分矩阵，得到完整的评分数据。

步骤4使用LSHBMRPK-means算法对完整的用户-项目评分数据进行聚类。

步骤5将目标用户与各聚类中心进行比较，找出目标用户的所属分类。

步骤6在相似度较高的各簇中查找最近邻居，生成推荐。

步骤7对推荐结果进行分析和测评。

4.3 确定正确的聚类算法的簇个数

确定正确的簇的个数。将误差的平方和SSE（公式（3））作为度量聚类质量的函数。

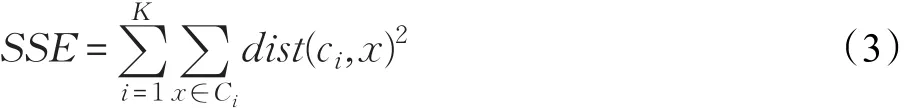
其中x代表对象，K是簇的个数，Ci表示第i个簇，ci是簇Ci的质心。dist是两个对象之间的欧几里得距离。SSE的值越小，表明聚类效果就越好。但簇个数不能过大，同时也不能过小，因而选择合适的簇个数对聚类的结果很关键。通过选取不同的初始簇个数，计算出相应的误差平方和，得到簇个数的SSE曲线，如图3所示。

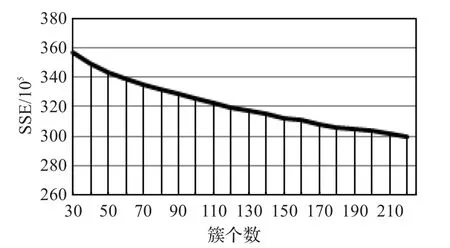
图3 簇个数的SSE曲线

图3 中，横坐标表示簇的个数，纵坐标是对应的误差平方和。从图可以看出，当簇个数为160时，SSE曲线下降的比其他点要多些，之后随着簇个数的增加，SSE的值变化减少。因此本实验的簇数选为160。

4.4 测试LSHBMRPK-means算法的执行时间

分别在不同集群规模环境下对LSHBMRPK-means算法进行测试，并对实验结果进行分析。测试MapReduce并行化的算法的有效性，和节点数对并行化算法的影响。

对同一数据集，不同节点数对应的算法执行时间如图4所示。

图4 不同节点数与执行时间测试结果

从图4看到不同的节点数对应的算法执行时间。测试结果可以看出，多个节点环境相比于单个节点环境，算法的执行效率得到了极大提高。在集群环境下，随着节点数的不断增加，LSHBMRPK-means算法生成聚类结果的时间也会减少。此外，实验结果说明LSHBMRPK-means算法有很好的扩展性和加速比。

4.5 测试局部敏感哈希算法的有效性

通过局部敏感哈希函数生成的代表点，相比于原始的数据集，规模要减少很多，同时，代表点集的数据质量比较高，能够很好地代表原始数据集，在降低数据规模的同时，也能提高聚类的质量。本实验内容是将基于局部敏感哈希函数的MapReduce并行化的k-means聚类算法与未经过局部敏感哈希函数处理的MapReduce并行化的k-means聚类算法的性能进行比较，通过分析两者的执行时间，以测试局部敏感哈希函数的有效性。

对同一数据集和相同节点数，基于局部敏感哈希函数的MapReduce并行化的k-means聚类算法与没有经过局部敏感哈希函数处理的MapReduce并行化的k-means聚类算法的执行时间进行比较，测试结果如图5所示。

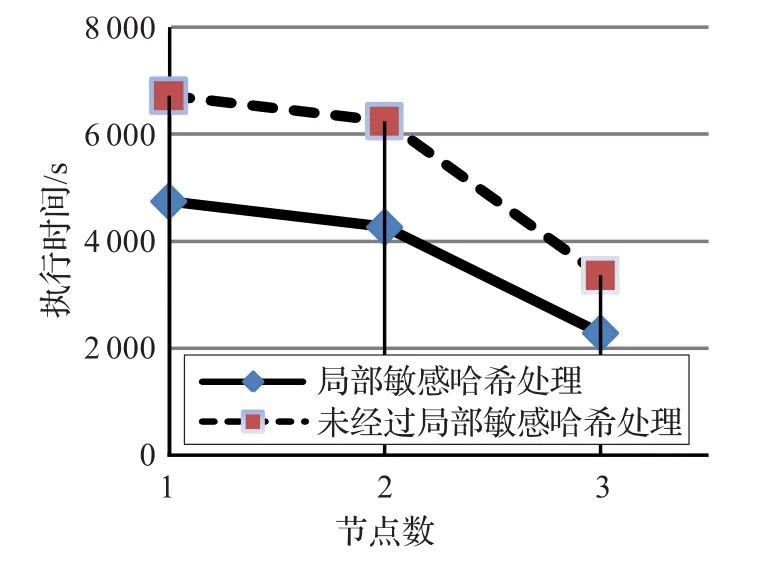
图5 算法执行时间测试结果

从两者的测试结果可以看出，由于局部敏感哈希降低了数据的规模，基于局部敏感哈希的MapReduce并行化k-means聚类算法在处理海量高维数据时具有很好的执行效率，同时也说明了通过局部敏感哈希函数生成的代表点集能够有效的代表原始数据集。

4.6 测试不同聚类个数对推荐性能的影响

使用LFM对评分矩阵进行填充补全后，使用LSHBMRPK-means算法对评分数据以用户为向量进行聚类操作。通过实验，记录了推荐性能与聚类个数的关系如图6所示。

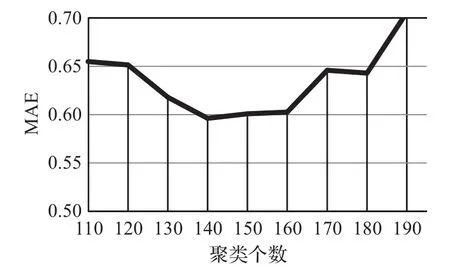
图6 推荐性能与聚类个数关系图

图6 中，横坐标表示聚类个数，纵坐标是其对应的平均绝对误差（MAE）。从聚类个数与MAE的关系曲线可以看出，随着聚类个数的增长，MAE先减少，后又上升，在聚类个数为140左右时，MAE达到最低点，此时，推荐质量最高。

5 结束语

本文针对基本的k-means聚类算法在处理大数据时的不足，提出了LSHBMRPK-means算法。实验证明LSHBMRPK-means算法具有较好的可扩展性，且局部敏感哈希函数能够有效降低数据的规模，提高计算效率。并将LSHBMRPK-means算法应用到基于聚类的推荐算法中，解决推荐算法的可扩展性问题。同时针对评分数据的稀疏性问题，本文使用LFM方法对评分数据集中的缺失值进行填充。通过实验证明基于LFM的LSHBMRPK-means协同过滤算法具有较好的可扩展性，同时解决了因评分数据稀疏导致推荐准确率不高的问题。

[1]孟小峰，慈祥.大数据管理：概念，技术与挑战[J].计算机研究与发展，2013，50（1）：146-169.

[2]Tan P N，Steinbach M，Kumar V.数据挖掘导论[M].北京：人民邮电出版社，2006.

[3]Dean J，Ghemawat S.MapReduce：simplified data processing on large clusters[J].Communications of the ACM，2008，51（1）：107-113.

[4]Datar M，Immorlica N，Indyk P，et al.Locality-sensitive hashing scheme based on p-stable distributions[C]//Proceedings of the Twentieth Annual Symposium on Computational Geometry.ACM，2004：253-262.

[5]李秋虹.基于MapReduce的大规模数据挖掘技术研究[D].上海：复旦大学，2013.

[6]项亮.推荐系统实战[M].北京：人民邮电出版社，2012：1-2.

[7]Balabanovic M，Shoham Y.Learning information retrieval agents：Experiments with automated web browsing[C]//On-line Working Notes of the AAAI Spring Symposium Series on Information Gathering from Distributed，Heterogeneous Environments，1995：13-18.

[8]Golub G H，Reinsch C.Singular value decomposition and least squares solutions[J].Numerische Mathematik，1970，14（5）：403-420.

[9]夏培勇.个性化推荐技术中的协同过滤算法研究[D].山东青岛：中国海洋大学，2011.

[10]Aggarwal C C，Yu P S.Finding generalized projected clusters in high dimensional spaces[C]//ACM Sigmod International Conference on Management of Data，2000，29（2）：70-81.

[11]Aggarwal C C，Hinneburg A，Keim D A.On the surprising behavior of distance metrics in high dimensional space[M].Berlin Heidelberg：Springer，2001.

[12]Verleysen M.Learning high-dimensional data[J].Nato Science Series Sub Series III Computer and Systems Sciences，2003，186：141-162.

[13]Steinbach M，Ertöz L，Kumar V.The challenges of clustering high dimensional data[M]//New directions in statistical physics.Berlin Heidelberg：Springer，2004：273-309.

[14]Donoho D L.High-dimensional data analysis：The curses and blessings of dimensionality[J].AMS Math Challenges Lecture，2000：1-32.

[15]Rajaraman A，Ullman J D.Mining of massive datasets[M].Cambridge：Cambridge University Press，2012.

[16]黄震华，张佳雯，田春岐，等.基于排序学习的推荐算法研究综述[J].软件学报，2016，27（3）：691-713.

[17]丁祥武，郭涛，王梅，等.一种大规模分类数据聚类算法及其并行实现[J].计算机研究与发展，2016，53（5）.

[18]鲁法明，曾庆田，段华，等.一种并行化的启发式流程挖掘算法[J].软件学报，2015，26（3）：533-549.

[19]Har-Peled S，Indyk P，Motwani R.Approximate nearest neighbor：Towards removing the curse of dimensionality[J].Theory of Computing，2012，8（1）：321-350.

[20]Indyk P，Motwani R.Approximate nearest neighbors：Towards removing the curse of dimensionality[C]//Proceedings of the Thirtieth Annual ACM Symposium on Theory of Computing.ACM，1998：604-613.

[21]Zhao Weizhong，Ma Huifang，He Qing.Parallel k-means clustering based on mapreduce[C]//International Conference on Cloud Computing，2009：674-679.

LUO Jun,LI Jinhua

College of Data Science and Software Engineering,Qingdao University,Qingdao,Shandong 266071,China

LSHBMRPK-means algorithm and its application.Computer Engineering and Applications.Computer Engineering and Applications,2017,53（21）：62-67.

To deal with the problems that time complexity is extremely high and the result of clustering ispoor when basic k-means algorithm is used to handle on big data issues,the paper proposes LSHBMRPK-means algorithm,locality sensitive hashing-based MapReduce parallelized k-means algorithm.Due to the scalability problem of recommendation system,the paper applies LSHBMRPK-means algorithm to cluster-based collaborative filtering algorithm.In addition,to handle on the issue of sparsity in the rating dataset,the paper uses the method of LFM to fill in the sparse rating dataset,and proposes LFM-based LSHBMRPK-means collaborative filtering algorithm.Primary experiments show that LSHBMRPK-means can improve the efficiency and quality of clustering,the proposed algorithm combined with the filtering algorithm has a good scalability,and at the same time it has solved the problem of poor clustering quality caused by the sparse rating dataset.

big data;k-means;locality sensitive hashing function;MapReduce;recommendation algorithm

A

TP311

10.3778/j.issn.1002-8331.1605-0227

罗俊（1989—），男，硕士研究生，研究领域为软件开发方法与技术；李劲华（1963—），通讯作者，男，博士，教授，研究领域为软件工程、软件理论、数据科学，E-mail：lijh@qdu.edu.cn。

2016-05-18

2016-10-11

1002-8331（2017）21-0062-06

CNKI网络优先出版：2016-12-02,http://www.cnki.net/kcms/detail/11.2127.TP.20161202.1503.030.html