小学数学运算技能教学的三个层次
钟建林

《〈义务教育数学课程标准(2011年版)〉解读》提出:“能够按照一定的程序与步骤进行运算,称为运算技能。”[1]学生对运算程序和步骤的理解、掌握是一个漫长且不断发展的过程。从运算对象看,先是小学低年级的整数四则运算,然后逐步发展到小数、分数的四则运算,再到初中阶段的有理数运算、乘方和开方等运算,是从低到高、从具体到抽象的过程;从学生心理发展看,学生在学习不同运算内容时处于不同的年龄发展阶段,具有同样的发展脉络;从数学发展历程看,人类对运算技能的掌握是遵循着一定层次发展的过程。
布鲁纳建构了“经验之塔”,并坚持“教学的过程首先应从直接经验入手,然后是经验的映象性表象,再过渡到经验的符号性表象”的观点。他将各种教学活动归纳为动作性、映像性和抽象性活动三个类别,塔的最下层是动作性学习,包括各种直接的、参与性的学习活动,必须亲身经历,获得真实的感受;塔的中间层次是映像性学习,指用直观表象操作代替实物操作的学习,包括各种形象直观、声音直观等可用多媒体技术表现出的视听材料的学习;顶层是抽象性学习,它包括“经验之塔”中最上面两层所涉及的学习媒介[2]。
运算技能的发展也呈现出从动作性思维向映像性思维到抽象性思维发展的过程。笔者认为,学生的运算能力发展整体上呈现的是这样的态势——从低级到高级、从具象到抽象、从简单到复杂,要经历实物操作、图示理解、符号表达的过程,符合从动作性到映像性再到抽象性的学习规律。虽然这些不同层面的学习活动在某些内容的学习中会交织在一起共同发挥作用,但不同阶段的学习仍然呈现明显的阶段性特征。
一、借助实物,进行动作性学习
动作性学习,指通过动作(操作活动)进行运算技能的感知、理解和掌握。张兴华老师在《儿童学习心理学与小学数学教学》一书中介绍了他们进行的一项观察实验,从另一个侧面验证了皮亚杰的理论“智慧自动作发端”[3]。
实验的过程是这样的:在孩子们面前摆上一堆积木,然后观察他们的反应。孩子们并没有如人们想象的那样静下心来认真地进行观察,也没有试图按积木的颜色、形状等对它们进行分类,以便抽象出某些积木的共同属性,直至形成相关概念。他们几乎都不自觉地伸手拿起积木,认真地把玩起来。有的将积木一块块叠起来,拼摆着什么;有的从中取出一些,不停地比划着;也有的用积木互相敲打着、碰撞着……原来,孩子们正是在这样一种“动手操作”的过程中积累起对客观事物的感性认识,并逐渐形成有关它们的数量关系及位置、大小等空间形式,从而获得对外部世界的最初认识。
课堂里的实践操作是一种特殊的认识活动。一方面,它须要协同手与眼的活动,动态地感知客观事物;另一方面,它要密切沟通手与脑的活动,是把借助肢体的外部活动内化为以内部语言为主要形态的智力活动。操作活动在推进学生内化知识意义、发展逻辑思维与空间观念、加强意义识记等方面发挥积极作用。因此,在小学低年级的运算教学中,让学生经历摆一摆、圈一圈、画一画、数一数等数学活动过程,是初始运算教学时应该遵循的基本规律。如教学“5减去2”时,教师可设计如下动作性层面的操作活动:伸出5根手指,扳回2根手指,还伸着3根手指;有5根小棒,拿走了2根,还剩3根;有5颗糖果,吃掉了2颗,还剩3颗;树上有5只小鸟,飞走了2只,树上还有3只小鸟;5颗珠子,取走2颗,还剩3颗珠子;等等。
动作层面的操作活动一般具有以下特点:一是动作性,能够用生活中原生态的动作表示;二是情境性,即有着特定的情境;三是独特性,也可以称之为单一性,即这一阶段的操作对象往往只代表自身。须要注意的是,借助实物操作常常具有一定的局限性:一方面并不是所有的运算过程都能借助实物操作体现;另一方面实物种类太少时,容易导致学生难以脱离具体的实物理解算理,形成对实物的依赖。
二、借助图示,进行映像性学习
映象性学习,即通过对图(图形、图例、图表、头脑中的思维图式等)的操作进行运算技能的感知、理解和掌握。这个层面是学生的运算从动作性思维到映像性思维的过渡和交织阶段,仍有许多操作,但操作的对象已从具体实物逐步转向数学对象,如从苹果、小棒等生活中的具象性物体向圆形、正方形、线段等图形或具有抽象意义的对象转变。
这时的学习活动,仍然具有明显的操作性学习特征,但是操作对象已经具有一定的虚拟性和抽象性,具有明显的结构性特征,蕴涵着操作中各种对象的数量以及不同动作之间的隐性关系。如同样是“5-2”的学习,图示层面的活动如图1:有5个圆片,从中划去2个。这时的活动,操作对象从实物变为图形,动作从拿走、吃掉、飞走等原生态的生活行为转变为具有抽象意义的“划去”,甚至可以转化为涂色。
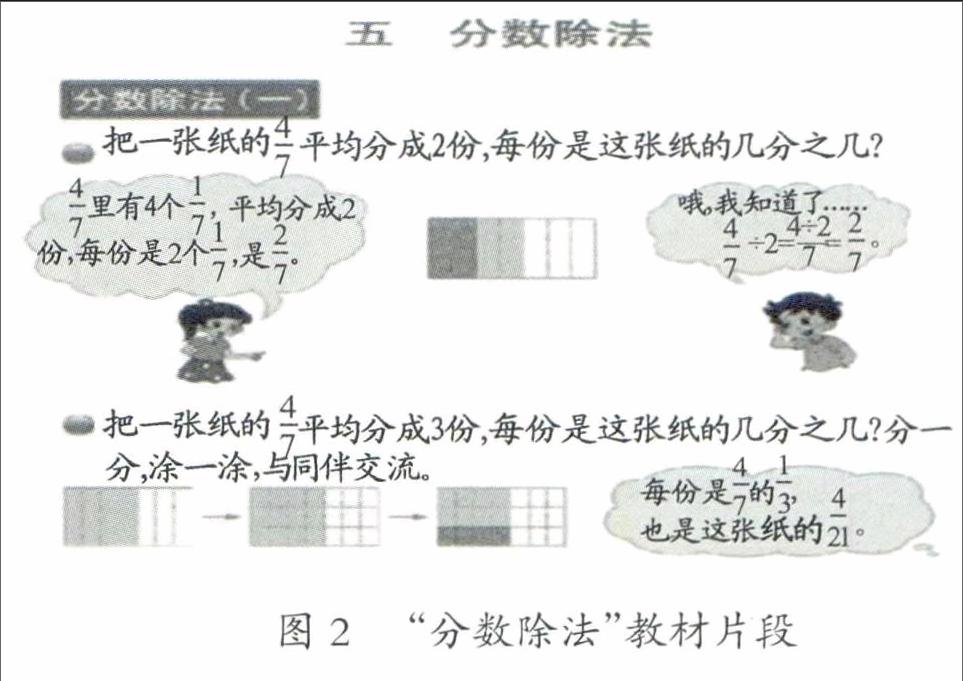
图示不仅能提炼动作性操作的思维含量,而且能化抽象为直观,使某些生活中较难找到实例或者较难用动作性学习完成的内容变得形象、直观。如北师大版的《数学》五年级下册“分数除法(一)”的教学[4](图2)。
三、借助符号,进行抽象性学习
抽象性学习,主要指借助数学符号等完成的运算。这里的符号,既包括数字1、2、3、4……也包括字母、运算符号等数学语言,如∑、≌、∞、∈、∮等。抽象性学习主要通过符号进行。如关于加法,《〈义务教育数学课程标准(2011年版)〉解读》给出这样的符号表达:“加法的定义:对于a,b∈N,规定运算a+b表示在a的后面增加b个的序数,如果这个序数为c,那么,称c为a与b的和。求和的运算叫做加法,记作:a+b=c”[1]。这显然超越了具体的动作性和映像性层面,进入了抽象性层面。这是完全基于抽象概念和逻辑的高级抽象性学习,小学生还无法适应,但是随着学生数学学习的深入,纯数学符号层面的运算内容逐渐地多起来,这是因为:一方面,学习的内容抽象程度越来越高,越来越需要超脱具体形象束缚的运算技能;另一方面,学生的年龄已经能够适应形式运算阶段的运算需要。
抽象性学习与抽象性有关,但也有着明显不同。一般来说,在运算技能教学中,抽象有三个层次:一是以抽象的物体表示具体的物体,如在低年级的运算学习过程中常常用小棒或者圆片表示动物、水果等;二是以抽象的数字或符号表示有形的物体或动作,如用1、2、3等表示数,用“+”“-”等表示运算,属于观念性、抽象性较强的操作;三是以抽象的符号表示某种关系或者规律,如y=kx(k不等于0),“-5”表示负5等。
映象性学习在动作性学习阶段的抽象和思维活动中已经存在。但是,抽象性学习主要指借助数学化程度较高的符号完成的思维含量较高的学习活动。在运算技能学习中,抽象性学习主要指脱离实物和具体情境进行的运算,如纯数字的计算、字母表示的运算规律等。
从动作性、映像性和抽象性的角度考虑,小学阶段的运算技能呈现出以下特点:一是阶段性递进的特点。总体趋势上,年级越低动作性技能越突出,年级越高抽象性技能越明显。二是多元并存的特点。用计算解决某种问题或探究某类运算规律时,通常存在不同层次的策略,如计算“9+几”时就同时存在这三个层次的策略。三是相互渗透性。学生对运算技能的掌握有不同层次,这三个层次内部存在着递进性和发展性,但相互间又不是完全割裂的,呈相互交织、螺旋上升的态势。
参考文献
[1] 教育部基础教育课程教材专家工作委员会.义务教育数学课程标准(2011年版)解读[M].北京:北京师范大学出版集团,2012.
[2] 孔凡哲,曾峥.数学学习心理学[M].北京:北京大学出版社,2009.
[3] 张兴华.小学数学教学心理学:儿童学习心理与小学数学教学[M].南京:江苏教育出版社,2011.
[4] 义务教育数学课程研制组.数学(五年级下册)[M].北京:北京师范大学出版社,2012.
[責任编辑:陈国庆]endprint

