时域物理光学后向散射近场线积分表达式

郭广滨 郭立新

(西安电子科技大学物理与光电工程学院,西安 710071)

时域物理光学后向散射近场线积分表达式

郭广滨 郭立新

(西安电子科技大学物理与光电工程学院,西安 710071)

提出了一种计算偶极子源照射时理想导体平板后向散射近场的时域物理光学(Time-Domain Physical-Optics, TDPO)线积分表达式．利用并矢分析中的面梯度定理和面散度定理,将TDPO面积分表达式化为线积分表达式．该表达式消除了积分中的奇异性,适用于偶极子天线处在任意位置处的情形．计算了导体平板和复杂目标的瞬态后向散射场,与其他方法结果吻合良好．数值结果表明,该方法在保证计算精度的前提下,可以大大提高计算效率．

时域物理光学法;后向散射;近场;线积分

引 言

随着短脉冲通信和超宽带雷达系统的广泛应用,采用时域方法来分析目标的瞬态电磁散射已成为计算电磁学中的热点之一．时域物理光学(Time-Domain Physical-Optics, TDPO)由于计算速度快、所需内存小,被广泛用于分析电大目标的瞬态电磁散射,尤其是目标的近场电磁散射特性越来越受到人们的重视．周晓[1]从时域Maxwell方程出发,推导出了时域电磁场面积分方程,进而获得了TDPO面积分表达式,采用数值积分技术,该表达式理论上可以计算任意分布源照射情况下,任意观察点处的目标散射场．然而,随着散射表面电尺寸的逐渐增大,数值积分技术的计算时间会急剧增加．为了减少计算时间,必须采用一些加速算法,目前主要有两种加速算法来处理近场散射问题,概括起来为:1)面元法;2)面积分退化为线积分．

面元法的思想是将积分面剖分成小面元,使得观察点位于每一个小面元的远场区,然后利用Gordon公式计算每一个小面元的散射场,进而得到散射总场．文献[1]把Legault基于面元远场近似的思想引入到时域近场计算,提出了一种基于面元局部格林函数近似的TDPO快速近场计算公式,给出了TDPO积分的近场闭合形式．虽然该方法在一定程度上可以提高计算速度,但由于其使用了远场近似,势必会损失一些精度,而且当观察点距离目标越近时,剖分面元的尺寸就会越小,这在一定程度上也会降低计算速度．

第2种方法又称为线积分技术,该方法把二维面积分降维成一维线积分,从而把计算时间从随电尺寸的平方关系变化加速到线性关系,经典的线积分技术——M-R(Maggi-Rubinowicz)变换[2-6]早在几十年前就被提出．Johansen and Breinbjerg利用M-R变换推导了偶极子波照射下理想导体的物理光学散射场[6],Fan根据Asvestas的频域推导过程[5],推导出了M-R变换的时域表达式[7],给出了偶极子照射下理想导体的TDPO散射场表达式．然而,这些根据M-R变换所推导出的线积分表达式不适用于观察点和源点处于同一位置处的情况．Fan改进了Gordon的工作[8],引入矢量定理,提出了一种计算后向散射(观察点和源点处于同一位置)的频域物理光学线积分表达式[9]．

本文基于TDPO面积分表达式,根据文献[9]中的方法,推导了其时域线积分表达式,给出了偶极子天线辐射下理想导体平板后向散射近场的线积分表达式．

1 线积分公式的推导

根据文献[1]中的时域电磁场面积分表达式,可以得到理想导体的TDPO散射场表达式为:

(1)

(2)

以电偶极子辐射为例,如图1所示,位于r处的电偶极子的时域辐射磁场为[10]

(3)

式中:p(t)为激励脉冲信号;“*”代表卷积;α为偶极矩;ρ=r′-r;δ(t)是冲击函数;c为波速．

图1 偶极子照射导体平板空间参数几何示意图

为了求解方便,本文以散射磁场Hs(r,t)的面积分表达式为例,推导其线积分表达式．将式(3)代入到式(2)中,可以得到电偶极子辐射时,理想导体的后向(R=-ρ)散射磁场为

(4)

当S′为金属平板时,散射磁场可以写为

[I1(r,t)+R⊥I2(r,t)]×α,

(5)

(6)

(7)

1) 面梯度定理

∬S‖

(8)

2) 面散度定理

∬S‖

(9)

图2 单位矢量空间几何示意图

令

(10)

(11)

则式(6)～(7)可以写为:

I1(r,t)=∬Sf(t,R)dS′;

(12)

I2(r,t)=∬S·F(t,R)dS′．

(13)

对式(12)利用面梯度定理,对式(13)利用面散度定理,可以获得其线积分表达式为:

(14)

(15)

2 奇异点处理

1)由于R≠0,所以I1(r,t)不存在奇异性．

2)当观察点(天线位置)与平板处于同一平面内时,满足R⊥=0,R‖≠0,I2(r,t)取式(15)下面那一项,不存在奇异性．

(16)

式中:

3 数值算例

本节分别采用面积分表达式和本文提出的线积分表达式来计算目标的后向瞬态散射场,给出两个算例来说明本文提出的线积分表达式的正确性与高效性．为了定量地说明线积分表达式的计算精度,分别采用式(17)和式(18)计算两种结果的绝对误差和平均相对误差:

εA(ti)=|Hsi(ti)-Hli(ti)|;

(17)

(18)

式中:Nt为采样时间点总数;ti为第i个采样时间点;Hli为线积分计算结果;Hsi为面积分计算结果．

3.1导体平板后向散射

(19)

式中:τ=4/fb;t0=τ．高斯调制脉冲时域波形如图3所示．

图3 高斯调制脉冲时域波形

表1给出了两种积分表达式所需的剖分数N和计算时间(CPU频率为3.2 GHz),线积分和面积分的剖分数比为1∶500,计算时间比为1∶219．可以看出,相对于数值面积分方法,采用线积分技术不仅能保证计算精度,还可以大大减少计算时间．

图4 金属平板后向近场瞬态散射

(a) 早期散射场

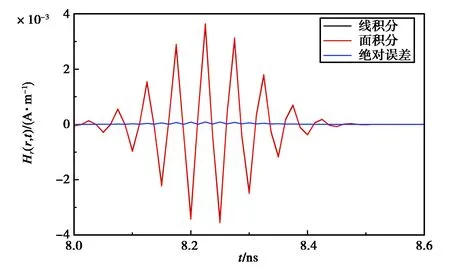
(b) 后期散射场图5 早期散射场和后期散射场的峰值区域

算法剖分数目计算时间/s线积分800055面积分400445012042

3.2复杂目标后向散射

图6 导弹几何模型

(a) Hr

(b) Hθ

(c) Hφ图7 导弹后向瞬态散射磁场

4 结 论

本文利用面散度定理和面梯度定理将偶极子辐射时理想导体平面后向散射近场的物理光学面积分表达式转化为线积分表达式,并且消除了奇异性．与传统面积分表达式相比,该表达式既可以保证良好的计算精度,又能大大提高计算速度．值得注意的是,该表达式目前只适用于偶极子源照射的情形,因而有必要把这一工作拓展至任意源照射的情形,以获得适用于近场计算的快速物理光学方法,这将是本文作者下一步的研究工作．

[1] 周晓. 基于TD-FIT与TD-SBR的瞬态电磁场混合算法[D]. 南京: 东南大学, 2016.

ZHOU X. Hybrid algorithm of electromagnetic transient analysisbased on TD-FIT and TD-SBR[D]. Nanjing: Southeast University, 2016. (in Chinese)

[2] MAGGI G A. Sulla propagazione libera e perturbata delle onde luminose in un mezzo isotropo[J]. Annali di matematica pura ed applicata(1867-1897), 1888, 16(1): 21-48. (in Italian)

[3] RUBINOWICZ A. Die beugungswelle in der kirchhoffschen theorie der beugungserscheinungen[J]. Annalen der physik, 1917, 358(12):257-278. (in German)

[4] ASVESTAS J S. Line integrals and physical optics. part I. the transformation of the solid-angle surface integral to a line integral[J]. Journal of the optical society of America A, 1985, 2(6): 891-895.

[5] ASVESTAS J S. The physical optics fields of an aperture on a perfectly conducting screen in terms of line integrals[J]. IEEE transactions on antennas and propagation, 1986, 34(9):1155-1159.

[6] JOHANSEN P M, BREINBJERG O. An exact line integral representation of the physical optics scattered field: the case of a perfectly conducting polyhedral structure illuminated by electric Hertzian dipoles[J]. IEEE transactions on antennas and propagation, 1995, 43(7): 689-696.

[7] FAN T T, ZHOU X, YU W M, et al. Time-domain line-integral representations of physical-optics scattered fields[J]. IEEE transactions on antennas and propagation, 2017, 65(1): 309-318.

[8] GORDON W B. Contour integral representation for near field backscatter from a flat plate[J]. IEEE transactions on antennas and propagation, 2012, 60(5): 2587-2589.

[9] FAN T T, ZHOU X, CUI T J. Singularity-free contour-integral representations for physical-optics near-field backscattering problem[J]. IEEE transactions on antennas and propagation, 2017, 65(2): 805-811.

[10] ERGIN A A, KARACA S. An exact time domain evaluation for radiated fields from a Hertz dipole[C]//2010 Mediterranean Microwave Symposium. Guzelyurt: IEEE, August 25-27, 2010.

[11] CHEN-TO T. Vector analysis on surface[M]//General vector and dyadic analysis: applied mathematics in field theory. Wiley-IEEE Press, 1997: 99-115.

郭广滨(1993—),男,山东人,西安电子科技大学博士生,研究方向为电磁散射、计算电磁学．

郭立新(1968—),男,陕西人,西安电子科技大学物理与光电工程学院教授,博士生导师,主要从事复杂目标与地、海环境电磁散射特性、随机介质中的电波传播特性、天线理论设计与微波技术研究工作．

Time-domainphysical-opticsline-integralrepresentationsofbackscatterednear-fields

GUOGuangbinGUOLixin

(SchoolofPhysicsandOptoeletronicEngineering,XidianUniversity,Xi’an710071,China)

A time-domain physical-optics(TDPO) line-integral representation is developed for the backscattered near-fields from a perfectly conducting surface illuminated by a dipole resource. The proposed representation is derived from time-domain physical-optics(TDPO) surface-integral representation by introducing two theorems: surface gradient theorem and surface divergence theorem. The proposed representation is free from singularities for all the source/observer positions in which the dipole antenna is located. The transient backscattered magnetic fields of metal plate and a complex object are computed. The results are in good agreement with those obtained by other methods. Numerical results show that the method can not only ensure the calculation accuracy, but also greatly improve the calculation speed.

time-domain physical-optics method; backscattering; near-field; line-integral

郭广滨, 郭立新. 时域物理光学后向散射近场线积分表达式[J]. 电波科学学报,2017,32(4):385-390.

10.13443/j.cjors.2017062201

GUO G B, GUO L X. Time-domain physical-optics line-integral representations of back scattered near-fields [J]. Chinese journal of radio science,2017,32(4):385-390. (in Chinese). DOI: 10.13443/j.cjors.2017062201

TN011

A

1005-0388(2017)04-0385-06

DOI10.13443/j.cjors.2017062201

2017-06-22

国家自然科学基金创新研究群体科学基金(61621005)；国家自然科学基金(41406201)

联系人： 郭广滨 E-mail: 726758809@qq.com