弱太阳闪烁对深空电波传播影响的预测模型
徐冠军 宋朝晖
(华东师范大学信息科学技术学院,上海 200241)
弱太阳闪烁对深空电波传播影响的预测模型
徐冠军 宋朝晖
(华东师范大学信息科学技术学院,上海 200241)
针对上合期间太阳风湍涡不规则性对穿过日冕区无线电波所引发的太阳闪烁问题,基于弱闪烁理论提出一种幅度起伏、相位起伏和到达角起伏的预测模型.该模型充分考虑了上合期间通信链路的几何模型、日冕背景参数和太阳风湍涡谱模型. 仿真结果指出,太阳风湍涡外尺度、湍涡谱指数对太阳闪烁有较大的影响. 太阳闪烁对无线电波的影响随日径距离的增大而逐渐减小,且随无线电波工作频率的提高而减小. 与实测数据的对比结果进一步表明,所提预测模型具有较高的精度,且其准确性随电波工作频率的增大而提高. 因此,提出的太阳闪烁预测模型可对未来的深空探测活动提供参考依据.
深空通信;无线电波;太阳闪烁;湍涡不规则性;日径距离
引 言
对宇宙空间的探索是人类探索宇宙起源、拓展生存空间的必由之路,而构建可靠的深空通信链路是未来深空探测的重要保障. 继20世纪50年代的探月计划后,目前包括美国国家宇航局(NationalAeronautics and Space Administration, NASA)、欧洲空间局(European Space Agency, ESA)、日本航天署(Japan Aerospace Exploration Agency, JAXA)和中国航空局(China National Space Administration, CNSA)在内的各研究机构纷纷推出规模宏大的深空探测计划[1-3]. 在深空探测中,无线电波需面对远距离通信带来的大传输延迟、大路径损耗,以及由此所引发的数据传输速率受限、接收端信噪比较低等问题. 此外,上合期间复杂日冕环境所引起的信号失真、链路中断等问题也给深空通信提出了极大的挑战[4-5]. 目前,为克服传输速率低所提出的通信策略已十分丰富,具体包括增大天线口径、提高通信频率、采用中继通信等,但对无线电波在日冕环境所受影响的研究却刚刚起步. 随着未来深空探测任务的逐渐增多,对无线电波受太阳风湍涡不规则性影响的研究变得日益紧迫.
行星聚合期间会出现太阳介于地球和行星探测器之间的情形,称之为上合[4]. 此时,往返于地球和探测器间的无线电波会穿过太阳日冕区,该区域太阳风湍涡的不均匀性将引起媒质介电特性的变化,进而使得链路无线信号出现散射、折射和传播路径的变化,并最终导致无线电波幅度和相位的快速变化. 此外,太阳风湍涡的不规则性也会引起无线电波波阵面的倾斜,使得接收端到达角出现起伏变化. 日冕区太阳风对穿过其中无线电波的幅度、相位和到达角等所引起的起伏变化称为太阳闪烁[6],太阳闪烁会影响接收端的跟踪能力,并引发信号失锁,该现象随无线链路逐渐接近太阳而变得越发明显. 根据闪烁强度的大小通常将其分为弱太阳闪烁和强太阳闪烁. 弱太阳闪烁时,电波幅度、相位和到达角的变化将引起通信误码率增大,而在持续的强太阳闪烁期间,无线链路会出现长时间的中断,严重危及通信链路的正常运行[7-8]. 为避免强太阳闪烁时电波传播的复杂性及求解的困难性,目前,相关学者依据Cassini号探测器在2000年的上合通信特点开展了弱太阳闪烁对电波传播影响的研究[9-10],并提出相应的编码方案以提高链路的通信质量[4, 9-11].
太阳闪烁对深空通信的影响虽已引起各研究机构的注意,但研究结果仍不完整,且并未提出统一的幅度起伏、相位起伏和到达角起伏预测模型. 为简化日冕区电波传播问题,本文仅考虑日径距离大于1个太阳半径时的弱太阳闪烁问题,并利用Rytov近似理论建立弱太阳闪烁下的幅度起伏、相位起伏和到达角起伏预测模型. 在此基础上,分析了日冕背景参数对太阳闪烁的影响,并定量分析了太阳闪烁的影响程度以及预测模型的准确性.
1 背景模型与日冕结构特性
1.1上合期间的几何模型与太阳风等离子体密度
在上合期间,往返于地球观测站和深空探测器间的无线电波会依次穿过地球大气层、地球电离层(含磁层)、行星际空间以及太阳日冕并最终到达天线接收端. 由表1所给出的日冕扰动和电离层扰动分别对深空通信的影响可知,无线电波在距太阳4Rsun(Rsun为太阳半径)时所遭受的影响要远大于电离层的影响. 此外,考虑到电离层等离子体密度(1×109~1×1012/m3)远小于日冕区太阳风等离子体密度(1×1012~1×1016/m3),且深空通信无线电波通常工作在S、X和Ka波段,故电离层的等离子体频率远小于无线电波的工作频率.因此,本文忽略电离层的影响而仅考虑日冕区太阳风等离子体对无线电波的影响.
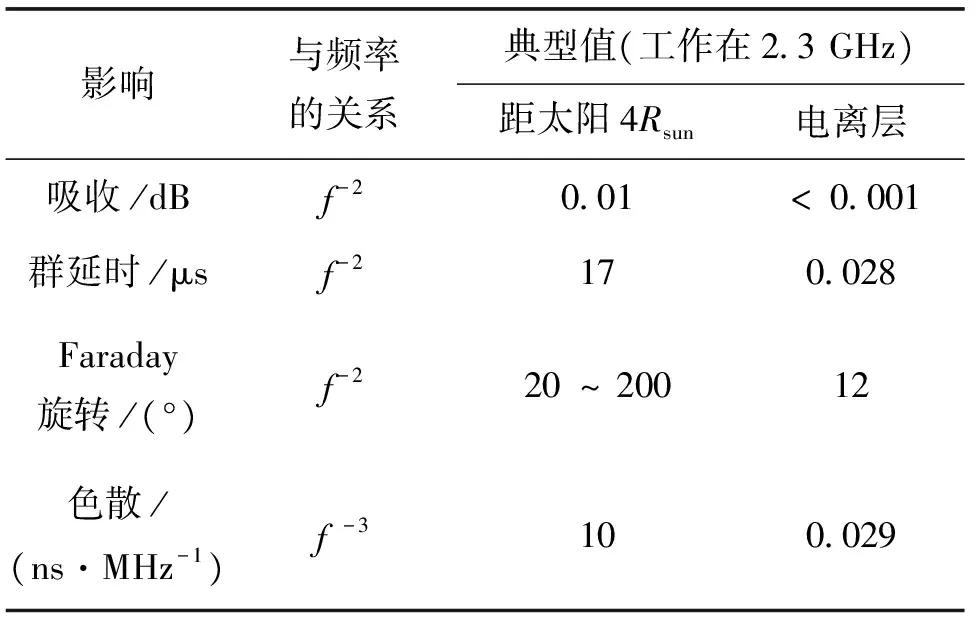
表1 日冕扰动和电离层扰动对深空通信的影响
图1给出了地球与探测器在上合期间的几何模型图.设太阳半径为Rsun(=6.96×108m),地球与太阳、探测器与太阳间的距离分别为Lse(=1.5×1011m)、Lsp.α和β分别表示太阳-地球-探测器(Sun-Earth-Probe,SEP)和太阳-探测器-地球(Sun-Probe-Earth,SPE)之间的夹角. 太阳与无线链路间的距离称为日径距离,且有r=Lsesinα,其通常以太阳半径Rsun为单位. 由图1所示的几何关系可知,地球与探测器间的距离L可表示为L=Lsecosα+Lspcosβ. 由图1还可知,SEP角随日径距离的减小而减小,在此过程中,无线电波受太阳风等离子体的影响将随之增大. 表2给出了2015年5月27日到2015年7月2日Rosetta号探测器在上合期间的几何特征.
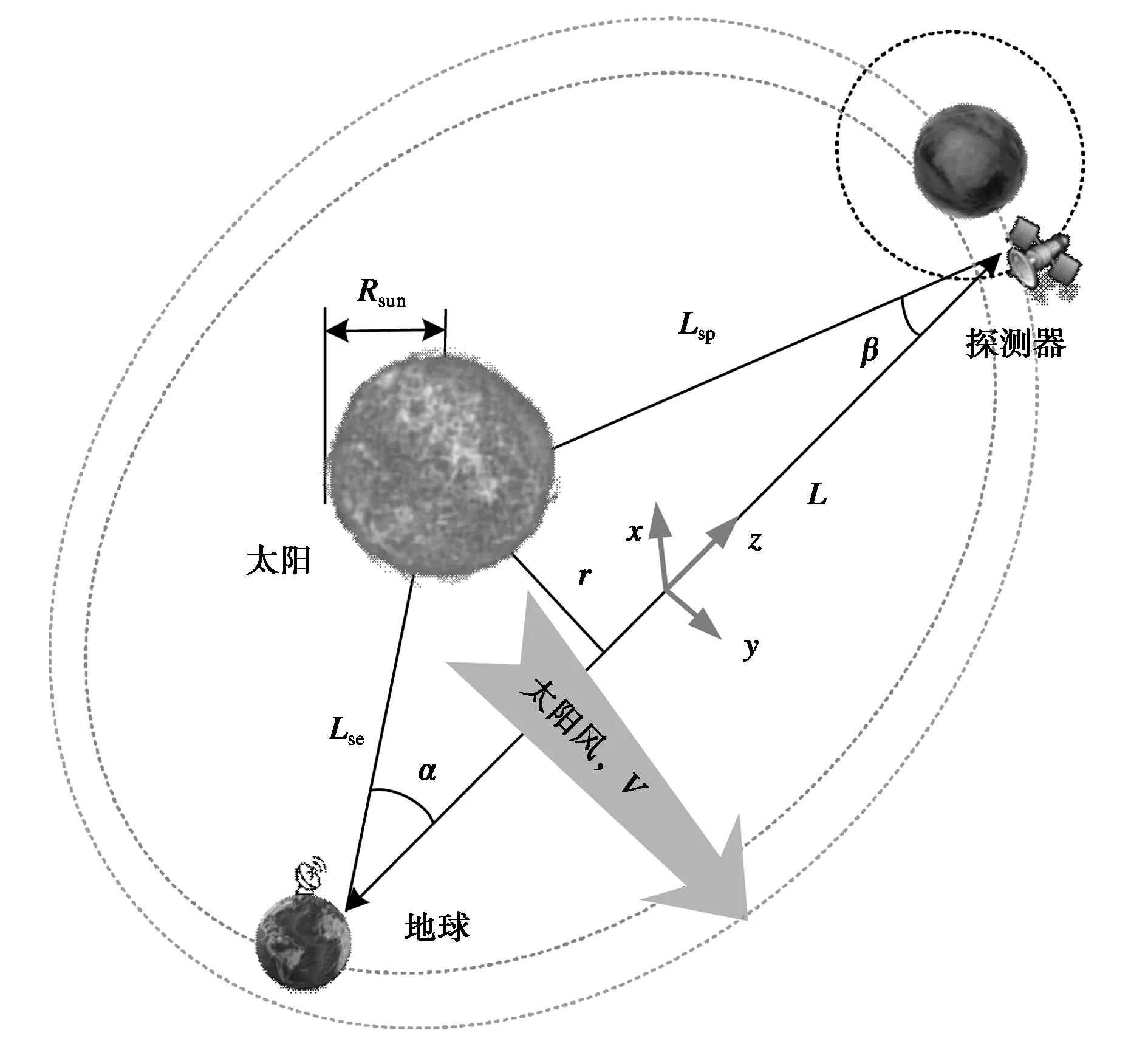
图1 上合通信的几何模型图

上合日期日径距离/RsunSEP角/(°)行星聚合动作2015⁃05⁃2712481进入上合2015⁃06⁃128079进入上合2015⁃06⁃143062进入上合2015⁃06⁃167079离开上合2015⁃07⁃0213506离开上合
太阳风湍涡沿太阳径向方向传输,并受诸如太阳热变化、太阳磁场、磁压以及太阳风加速等因素的影响而表现为湍涡的快速变化,其等离子体密度是一个连续的随机函数,在时间和空间尺度上快速起伏变化. 为简便起见,本文仅考虑太阳风等离子体在空间尺度上的变化. 天文研究者通过对日冕结构的长期观测和理论推导给出如下的太阳风等离子体密度模型[12]:
Ne(r,ξ)=Np(r)+[Ncs(r)-Np(r)]·
exp[-θ2/w2(r)]×106.
(1)
式中:ξ表示太阳磁场坐标系下日径距离r处的观测点与电流片的角距离[12];Np(r)和Ncs(r)分别为极区和电流片的等离子体密度;w(r)表示在太阳磁场坐标系下电流片的半角宽度[12].Np(r)、Ncs(r)、w(r)都是日径距离的函数,具体表达式为
(2)
1.2日冕区媒质介电特性
为简便起见,通常将太阳风等离子体密度表示为其背景均值部分和随机起伏部分δNe之和. 其中背景均值部分是引起无线电波群延迟、色散和Faraday旋转的主要原因,而随机起伏部分表征无线电波受太阳风湍涡不规则性所引起的随机变化,是导致太阳闪烁的主要因素. 根据Appleton-Hartree公式可知,太阳风等离子体密度的变化是引起其媒质介电特性变化的直接原因. 日冕区媒质电系数可表示为其均值量和起伏量的和,即
ε=〈ε0〉[1+δε(r)].
(3)
式中:〈ε0〉表示背景媒质介电常数在时间和空间变化下的系综均值;δε(r)为等离子体密度随机起伏所引起的相对介电常数的起伏变化量. 文献[7]指出,δε=reλ2δNe,其中,re是经典电子半径. 由上述公式可知,不同位置r和r′处相对介电常数起伏部分的相关函数可表示为

(4)
进一步由维纳辛钦定理可知,太阳风等离子体密度起伏量的空间相关函数与太阳风湍涡谱成傅里叶变换关系:
〈δNe(r)δNe(r′)〉= ∭d3κΦ(κ)
exp[iκ·(r-r′)].
(5)
式中,Φ(κ)是波矢量κ的三维空间谱. 为表征太阳风湍涡的功率谱密度,研究人员基于观测实验的基础提出了许多谱密度表达式并指出其为谱指数p的幂指数函数[13]. 为简便起见,本文仅考虑标量形式的波矢量κ和位置r,并引入广泛使用的Kolmogorov谱模型[9]:
(6)

exp[iκ·(r-r′)].
(7)
2 弱太阳闪烁下的闪烁预测模型
无线电波在随机媒质中的传播问题已受到广泛的研究[14-16],根据电波传播理论,太阳风等离子体不规则性将引起无线信号的散射与折射现象,进而导致幅度起伏、相位起伏和到达角起伏等. 考虑上合期间日径距离大于1Rsun的情形,此时穿过日冕区的链路折射角较小,太阳闪烁强度较弱,本部分将给出弱太阳闪烁下的幅度起伏、相位起伏和到达角起伏预测模型.
为求解方便,本文考虑以下假设[17]:1)日冕区太阳风湍涡不规则性的时间变化远比波的周期慢;2) 太阳风湍涡的特征尺度(外尺度)远大于电波波长. 因此,利用湍流统计理论中的“Taylor冻结理论”可以忽略湍涡媒质的时间变化量而仅考虑其空间变化.故,无线电波在太阳风湍涡中的波动方程可以表示为
(8)
式中,k=2π/λ是电波波数,λ为波长. 利用Rytov近似理论可求得该波动方程的迭代近似解,其电场强度可表示为无扰动的电场强度E0与其幂指数项exp(φ(r))的乘积. 根据上述弱闪烁下的假设条件,位置R处的电场强度可表示为[18]
E(R)=E0(R)exp-k2∭d3rδε(r)G(R,r).
(9)
为表述方便,本文仅考虑电场的标量形式,并使用对数幅度起伏χ=ln(E-E0)代替幅度起伏.考虑如下形式的电场强度表达式:
E(R)=A(R)exp{i[φ0+φ(R)]}.
(10)
式中:A(R)为电场强度值;φ0和φ(R)分别表示相位起伏均值及其起伏量. 故幅度起伏方差和相位起伏方差的系综均值可表示为[18]:
〈χ〉=-k2∭d3rδε(r)Re[G(R,r)].
(11)
〈φ〉=-k2∭d3rδε(r)Im[G(R,r)].
(12)
式中,Re[G(R,r)]和Im[G(R,r)]分别表示格林函数的实部和虚部. 考虑到幅度起伏、相位起伏和到达角起伏的均值为0,通常使用其方差量来表征其起伏大小. 因此,幅度起伏方差〈χ2〉和相位起伏方差〈φ2〉可分别表示为:

(13)

(14)
式中,A(R,r)=1-(4πz)cos[kr2-(2z)];B(R,r)=1-(4πz) sin[kr2-(2z)];z为链路长度. 式中幅度起伏和相位起伏的单位分别是Np和rad. 将式(7)分别代入到式(13)和(14)并进行三维积分变化,可得简化后的幅度起伏方差和相位起伏方差预测表达式为
(15)
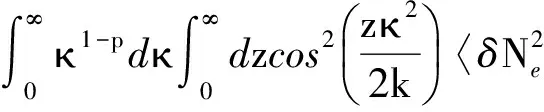
(16)
为进一步表征太阳闪烁对无线电波的影响,本文引入闪烁指数的概念,其定义为无线电波电场强度起伏的均方根值与其电场强度均值的比值,即归一化的幅度起伏方差.因此,闪烁指数可以表示为[18]

(17)
对式(15)和(16)进行傅里叶变换可得对应的幅度起伏谱和相位起伏谱函数. 文献[19]利用Tayler冻结理论指出,到达角起伏谱Wθ(ω)与相位起伏谱Wφ(ω)具有如下的函数关系:
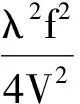
(18)
式中:V表示太阳风速度;ω是角频率. 因此,根据傅里叶逆变换可得简化后的到达角起伏方差预测公式为
(19)
式中,J1为一阶Bessel函数. 注意:推导所得的到达角起伏公式考虑了半径为ar的天线口径平滑效应的影响. 将公式(6)的太阳风湍涡谱模型代入到式(19)可进一步得到简化的到达角起伏公式. 由上述推导公式可知,幅度起伏、相位起伏和到达角起伏与太阳风湍涡不规则性〈δNe2〉、湍涡外尺度lo、湍涡谱指数p有关,且与电波波长的平方成正比例关系.
3 仿真讨论
3.1日冕背景参数对太阳闪烁的影响
本节将分析日冕背景参数(太阳风湍涡外尺度、谱指数)对太阳闪烁的影响. 研究表明太阳风速度是一个在时间和空间上快速变化的量,根据文献[20]的研究结果,本文取太阳风速度均值为400 km/s. 依据长期观测结果,太阳风湍涡谱指数主要分布于3.3~3.8,图2给出了不同探测器观测到的谱指数分布结果. 由图可知,谱指数与日径距离并无明显的联系. 相关文献[10, 13]指出,太阳风湍涡外尺度在1×103~1×106km. 依照NASA深空探测网的设计指标[21],设无线电波分别工作在S波段(2.3 GHz)和X波段(8.4 GHz),天线口径设置为35 m.
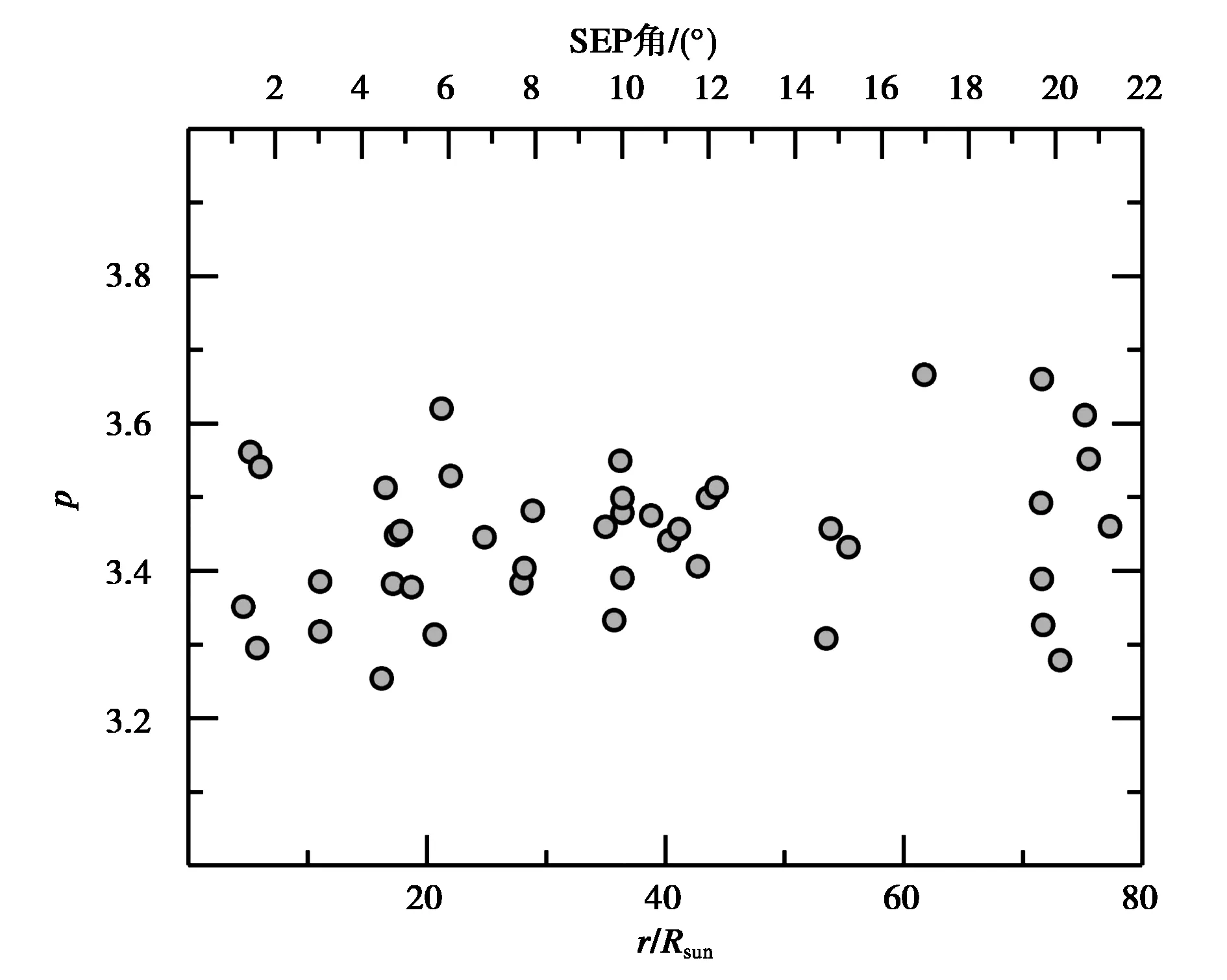
图2 不同探测器观测到的谱指数结果
图3、4和5分别给出了归一化的幅度起伏、相位起伏和到达角起伏随谱指数和太阳风湍涡外尺度变化的仿真结果.由图3、4可知,归一化的幅度起伏、相位起伏随湍涡外尺度的增加而减小,而在特定的谱指数下,图5中的到达角起伏几乎不随湍涡外尺度的变化而变化. 相对于湍涡外尺度的影响,谱指数对幅度、相位和到达角起伏的影响更为复杂. 由图4、5可知,相位起伏和到达角起伏随谱指数的增加而分别增大和减小. 当p=3.2时,图3中归一化的幅度起伏趋向于最大值,此后幅度起伏随谱指数的增加而逐渐减小,并在p=3.8时达到最小值. 上述现象主要是由于:无线电波随湍涡外尺度和谱指数的综合变化而逐渐进入湍涡惯性区,从而影响太阳闪烁的变化. 由上述分析可知,太阳风湍涡外尺度和谱指数对幅度、相位和到达角起伏有着较为复杂的影响,本文提出的太阳闪烁模型能在考虑太阳风湍涡外尺度和谱指数的影响下对幅度起伏、相位起伏和到达角起伏进行预测.
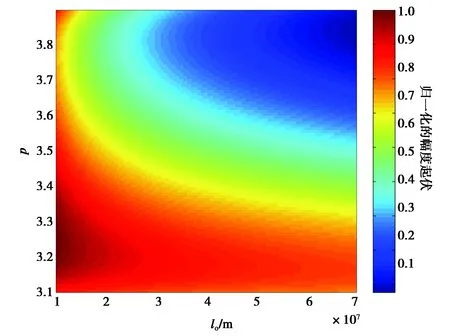
图3 归一化的幅度起伏随谱指数和湍涡外尺度的变化

图4 归一化的相位起伏随谱指数和湍涡外尺度的变化

图5 归一化的到达角起伏随谱指数和湍涡外尺度的变化
3.2太阳闪烁的定量分析
利用提出的闪烁指数模型,图6给出了工作在S和X波段下无线电波闪烁指数S4的预测值与实测数据的对比结果. 其中:谱指数p=11/3;图的横坐标正、负SEP角分别表示通信链路进入、离开上合阶段;实测数据来源于地面观测站对Mars Express号和Rosetta号分别在2004年9月和2006年9月飞行过程中所采集的数据[8].
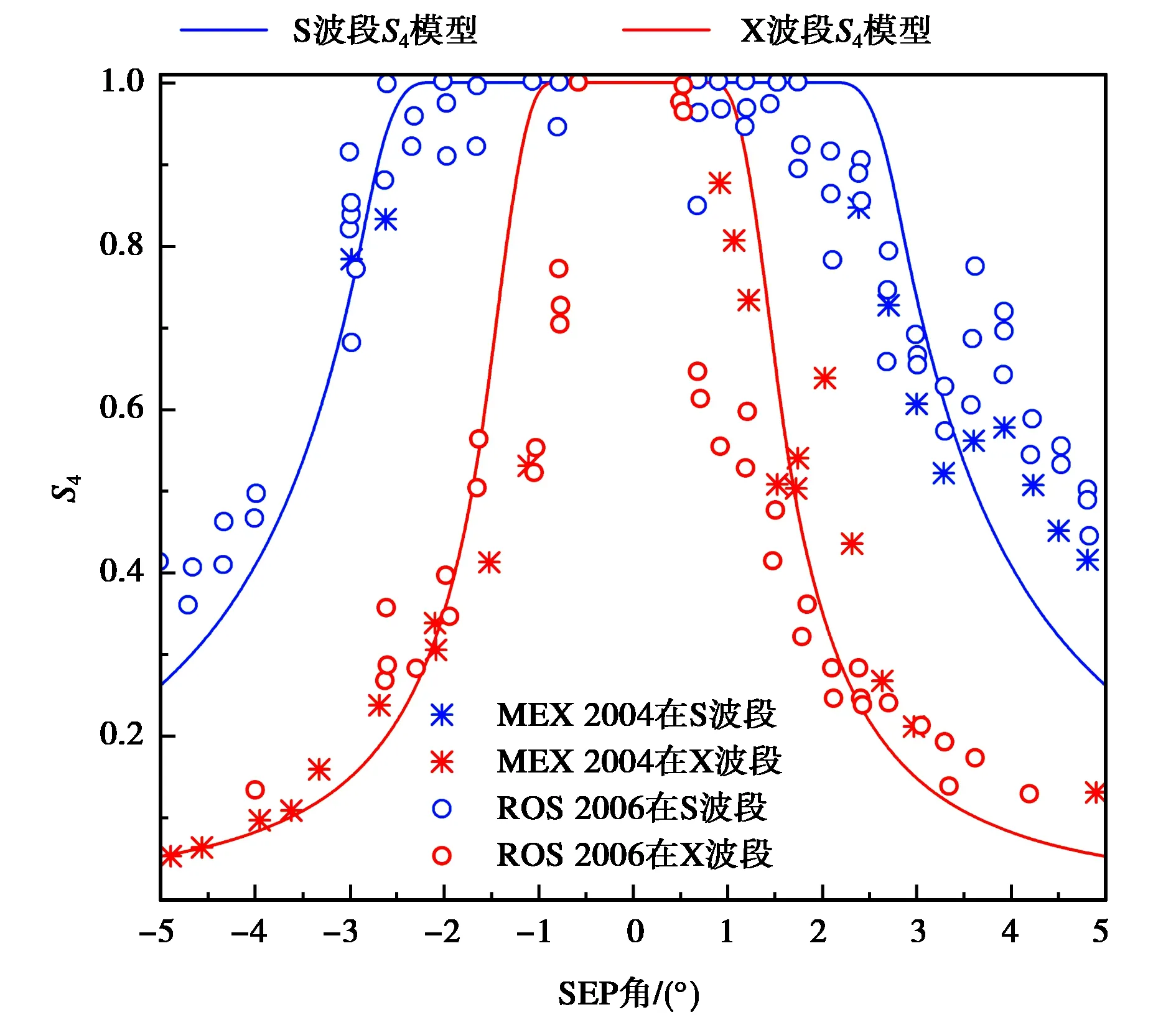
图6 所提闪烁指数预测模型与实测数据的对比图
由图6可知,闪烁指数随SEP角的减小而逐渐增大. 在相同的SEP角下,工作在X波段的无线电波相对于S波段具有更小的闪烁指数值. 当SEP角为2.5°和1.5°时,工作在S波段和X波段的无线电波分别趋于饱和(S4=1). 此外,提出的闪烁指数预测模型与实测数据具有相同的变化趋势,与Mars Express号和Rosetta号的实测数据相对比可知,所提模型在S波段和X波段的准确率分别为85%和92%. 上述结果表明,当无线电波工作在X波段时能有效降低闪烁指数的影响,且提出的闪烁指数预测模型在X波段具有更高的准确性.
图7给出了工作在S和X波段无线电波的相位起伏预测结果,其中实线表示预测值,符号标记为观测数据.可以看出,相位起伏随SEP角的减小而增大. 当SEP角为4°时,无线电波在S波段的相位起伏值为62 rad,而在X波段的相位起伏值仅为17 rad. 因此,提高无线电波工作频率可有效减小上合期间的相位起伏. 与文献[22]给出的X波段下不同SEP角的相位起伏观测结果相对比可知,提出的相位起伏预测模型在X波段的准确率为89%,且其准确性随SEP角的增大而提高.
图8给出了工作在S和X波段下无线电波的到达角起伏预测值随日径距离的变化.由图可知:到达角起伏随着日径距离的增大而逐渐减小;相比于S波段,工作在X波段的无线电波具有更小的到达角起伏值. 这意味着将无线电波工作频率提高到X波段能极大减小到达角起伏的影响.
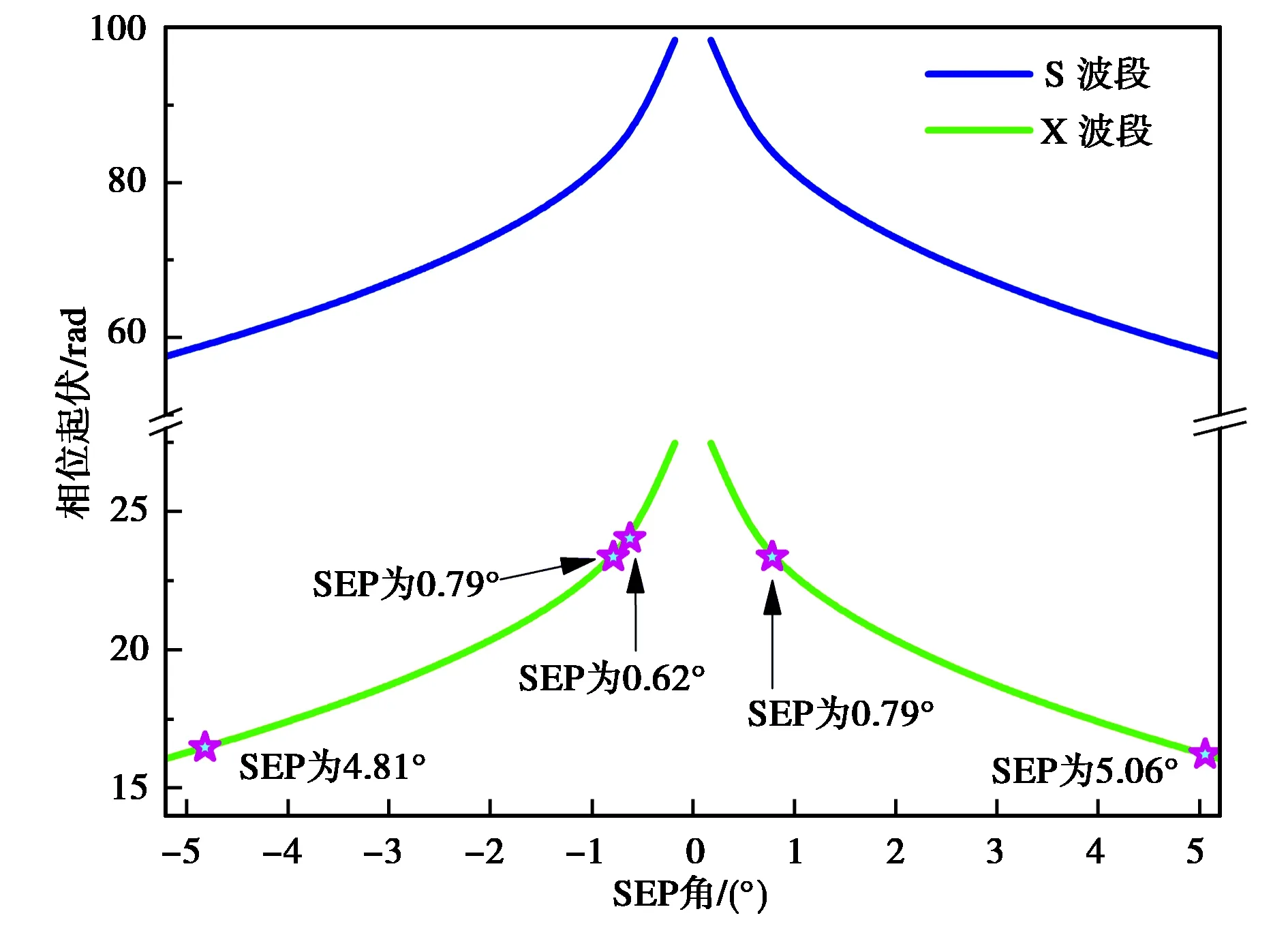
图7 工作在S和X波段下无线电波的相位起伏预测值 与实测数据的对比
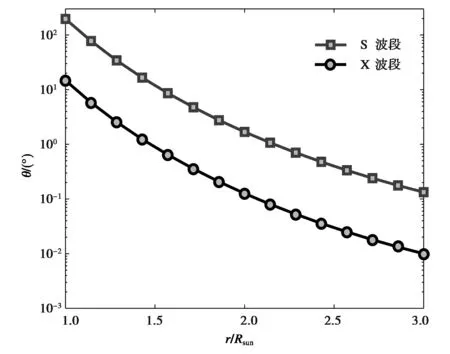
图8 工作在S和X波段下无线电波到达角起伏 随日径距离变化的关系图
由公式(15)、(16)和(19)可知,提出的幅度起伏、相位起伏和到达角起伏的预测模型是f-2的函数. 因此,增大无线电波工作频率可有效减小太阳闪烁的影响. 与实测数据的对比结果进一步表明,本文提出的太阳闪烁预测模型可有效预测未来深空探测活动中无线电波的幅度起伏、相位起伏和到达角起伏,从而为深空探测活动提供参考依据.
4 结 论
结合上合期间通信链路的几何模型和日冕背景参数特点,本文分别给出上合期间太阳风湍涡不规则性对无线电波幅度起伏、相位起伏和到达角起伏的预测模型. 通过引入具体的太阳风湍涡谱模型,本文探讨了湍涡外尺度和湍涡谱指数对太阳闪烁的影响. 仿真表明,提出的太阳闪烁预测模型与实测数据具有相同的变化趋势,且其预测精度随电波工作频率的增大而提高. 进一步分析可知,在未来探测活动中可通过增大无线电波工作频率来减小日冕区太阳风等离子体对电波信号幅度、相位和到达角起伏的影响.
[1] RAWSON S, FORNAROLI M, BOZZI M, et al. Future architectures for ESA deep space ground stations antennas[C]//The 5th European Conference on Antennas and Propagation. Rome:IEEE, April 11-15, 2011.
[2] WU W R, LIU W W, QIAO D, et al. Investigation on the development of deep space exploration [J]. Science China technological sciences, 2012, 55(4): 1086-1091.
[3] 张乃通, 李晖, 张钦宇. 深空探测通信技术发展趋势及思考[J]. 宇航学报, 2007, 28(4): 786-793.
ZHANG N T, LI H, ZHANG Q Y. Thought and developing trend in deep space exploration and communication[J]. Journal of astronautics, 2007, 28(4): 786-793. (in Chinese)
[4] LI Q, YIN L, LU J. Performance study of a deep space communications system with low-density parity-check coding under solar scintillation[J]. International journal of communications, 2012, 6(1): 1-9.
[5] 陆建华, 葛宁, 杜冰. 复杂性与不确定性: 无线通信面临的双重挑战[J]. 中国科学: 信息科学, 2013, 43(12): 1563-1577.
LU J H, GE N, DU B. Complexity and uncertainty: wireless communications face dual challenges[J]. Scientia sinica informationis, 2013, 43(12): 1563-1577. (in Chinese)
[6] XU G, SONG Z. A new model of amplitude fluctuations for radio propagation in solar corona during superior solar conjunction[J]. Radio science, 2016, 51(2): RS005769.
[7] HO C M, MORABITO D D, WOO R. Using phase scintillation spectral measurements to determine angle-of-arrival fluctuations during solar superior conjunction [J]. Radio science, 2010, 45(3): RS3005.
[8] MADDE R, MORLEY T, LANUCARA M, et al. A common receiver architecture for ESA radio science and delta-DOR support[J]. Proceedings of the IEEE, 2007, 95(11): 2215-2223.
[9] EFIMOV A I, SAMOZNAEV L N, BIRD M K, et al. Solar wind turbulence during the solar cycle deduced from Galileo coronal radio-sounding experiments[J]. Advances in space research, 2008, 42(1): 117-123.
[10] BISI M M, FALLOWS R A, BREEN A R, et al. Interplanetary scintillation observations of stream interaction regions in the solar wind[J]. Solar Physics, 2010, 261(1): 149-172.
[11] 吴桐, 闫毅, 李永成, 等. 太阳闪烁下深空信道建模与电波传播特性分析[J]. 电波科学学报, 2015, 30(3): 417-422.
WU T, YAN Y, LI Y C, et al. Deep space channel modeling and the analysis of wave propagation environment characteristics under solar scintillation[J]. Chinese journal of radio science, 2015, 30(3): 417-422.(in Chinese)
[12] THEJAPPA G, MACDOWALL R J. Effects of scattering on radio emission from the quiet Sun at low frequencies [J]. The astrophysical journal, 2008, 676(2): 1338.
[13] BASTIAN T S. Radio interferometric observations of scattering phenomena in the outer solar corona[C]//The 9th European Meeting on Solar Physics, Florence, 1999.
[14] KULIZHSKY A V. Uniform integral representation for the fluctuating field propagating through the multi-scale media[J]. Waves in random and complex media, 2016: 1-19. DOI: 10.1080-17455030.2016.1229874
[15] GRIMA C, BLANKENSHIP D D, SCHROEDER D M. Radar signal propagation through the ionosphere of Europa[J]. Planetary and space science, 2015, 117: 421-428.
[16] RINO C L, CARRANO C S. The application of numerical simulations in Beacon scintillation analysis and modeling[J]. Radio science, 2011, 46(3): RS004563.
[17] XU Z W, WU J, WU S, et al. Solution for the fourth moment equation of waves in random continuum under strong fluctuations: general theory and plane wave solution[J]. IEEE transactions on antennas and propagation, 2007, 55(6): 1613-1621.
[18] HO C M, WHEELON A. Amplitude scintillation due to atmospheric turbulence for the deep space network Ka-band downlink[R]. Pasadena: Jet Propulsion Laboratory, 2004.
[19] VILAR E, SMITH H. A theoretical and experimental study of angular scintillations in earth space paths[J]. IEEE transactions on antennas and propagation, 1986, 34(1): 2-10.
[20] MANOHARAN P K. Three-dimensional evolution of solar wind during solar cycles 22-24[J]. The astrophysical journal, 2012, 751(2): 128.
[21] NETWORK D S. DSN telecommunications link design handbook[R]. Pasadena: Jet Propulsion Laboratory, 2014.
[22] CALVÉS G M, POGREBENKO S V, CIMG, et al. Observations and analysis of phase scintillation of spacecraft signal on the interplanetary plasma[J]. Astronomy and astrophysics, 2014, 564(A4): 1-7.
徐冠军(1988—),男,安徽人,博士,主要从事深空通信、电波传播方向的研究.
宋朝晖(1970—),男,黑龙江人,博士,教授,主要研究方向为空间通信中电波传播理论、射频识别系统理论与技术、微波毫米波系统.
WeakensolarscintillationpredictionmodelforEMwavepropagationindeepspace
XUGuanjunSONGZhaohui
(SchoolofInformationScienceandTechnology,EastChinaNormalUniversity,Shanghai200241,China)
Electromagnetic(EM) waves propagating through the solar corona irregularities suffer solar scintillation during superior solar conjunction. Considering the geometric of the communication model, the corona structure and the turbulence spectral model, a prediction model for both amplitude fluctuations, phase fluctuations and angle-of-arrival fluctuations is proposed with the weaken scintillation theory. The simulation results demonstrate that the solar corona parameters, such as the spectral index and the turbulence outer scale have a tremendous impact on the fluctuations. Besides, solar scintillation increases with the decreasing of the heliocentric distance and its impact can be reduced by enhancing the EM waves frequency. Furthermore, the proposed model shows great agreement with the observed data and its accuracy increases when the radio frequency gets larger. Therefore, our solar scintillation prediction model can be effectively applied in the future deep space exploration.
deep space communication; electromagnetic waves; solar scintillation; turbulence irregularities; heliocentric distance
徐冠军, 宋朝晖. 弱太阳闪烁对深空电波传播影响的预测模型[J]. 电波科学学报,2017,32(4):377-384.
10.13443/j.cjors.2017072601
XU G J, SONG Z H. Weaken solar scintillation prediction model for EM wave propagation in deep space [J]. Chinese journal of radio science,2017,32(4):377-384. (in Chinese). DOI: 10.13443/j.cjors.2017072601
TN927
A
1005-0388(2017)04-0377-08
DOI10.13443/j.cjors.2017072601
2017-07-26
联系人: 宋朝晖 E-mail: zhsong@ce.ecnu.edu.cn

