磁化电离层等离子体异常吸收效应研究
满莉 马广林 车海琴
(中国电波传播研究所 电波环境特性及模化技术重点实验室,青岛 266107)
磁化电离层等离子体异常吸收效应研究
满莉 马广林 车海琴
(中国电波传播研究所 电波环境特性及模化技术重点实验室,青岛 266107)
研究了电离层加热中的异常吸收效应.采用动力学理论,从弗拉索夫方程出发,结合磁化等离子体中电波色散关系与地磁场中泵波电场作用于电子与离子形成的位移电流,详细推导了加热形成的沿磁场分布电子密度不均匀体扰动所引起的电波幅度异常吸收系数.利用异常吸收系数解析表达式模拟计算了吸收系数随地磁倾角的变化,结果表明:随着地磁倾角的增加,异常吸收系数增大,在地磁倾角约70°以后缓慢下降;在考虑了地磁场对高频电导率影响后,异常吸收系数降低,而且地磁倾角越大系数下降越明显.
电离层加热;异常吸收系数;磁化等离子体;动力学理论;地磁倾角
引 言
入射到电离层的大功率高频无线电波(称之为泵波)与电离层中等离子体相互作用,可引起局部电离层特性的变化,称之为电离层加热或电离层的人工变态[1].自“卢森堡效应”发现以来,电离层加热成为等离子体物理研究领域的热点之一,并基于在中纬与高纬地区所建立的多个加热装置,开展了大量实验与理论研究工作,观测到丰富的电离层非线性现象[2],如形成的沿磁场方向分布的电子密度不均匀体实现对HF/VHF/UHF信号的沿场散射,调制电离层电流形成“虚拟天线”实现VLF/ELF信号辐射与远距离接收,参量不稳定性形成的高频静电波通过波模变换产生丰富的受激电磁辐射现象,加热或加速电子与中性成分碰撞产生人工气辉辐射等,对实验现象的研究大大促进了等离子体非线性理论的发展.
异常吸收是最早观测到的电离层加热实验现象之一,是指除了欧姆吸收之外的吸收,表现为经过加热扰动区域的大功率泵波或接近泵波频率的小功率HF诊断波出现回波幅度的下降.早在1970年Cohen等[3]基于Platteville加热站观测到反射信号幅度的下降,该现象在多个加热站均得到复现[2,4-5].在电离层加热试验中,发现存在两种类型的异常吸收:第一种只出现在大功率O模泵波,其发生时间在毫秒量级;第二种在大功率O模电磁波和低功率诊断波均会出现[6].一般认为第一种异常吸收与参量衰变不稳定性 (Parametric Decay Instability,PDI)有关,第二种异常吸收则与热参量不稳定性(Thermal Parametric Instability,TPI)形成的人工不均匀体有关,大功率高频电波在电离层上混杂共振高度附近激发共振不稳定性与热参量不稳定性,从而形成人工沿磁场分布不均匀体,受人工沿磁场分布不均匀体影响入射到该区域的大功率高频电波与小功率的高频诊断波经波模转化过程形成被人工沿磁场分布不均匀体俘获的上混杂本征波,从而引起通过上混杂共振区域的高频电波幅度的异常吸收效应.Dawson与 Oberman[7-8]指出非热电离层不均匀体会显著提高等离子体电导率与阻抗.根据这一理论并结合Minkoff[9]实验测量的雷达后向散射系数,Graham等[10]提出O波异常吸收是入射的电磁波被加热形成的人工不均匀体散射转化为静电波引起的,并采用动理论方法得出异常吸收系数,但未考虑地磁场对位移电流的影响.Robinson等[11]结合实验测量结果反演获得人工不均匀体横向尺度与密度扰动信息.除了O波异常吸收外,后期实验观测到X波的异常吸收现象[12],为此,Zabotin等发展了中尺度电离层不均匀体X波多重散射异常吸收理论[13-14].Vas’kov等[15]数值计算了电子密度耗空的圆柱状沿磁场分布不均匀体引起的O波异常吸收效应,并考虑电子密度扰动对激发的冷Z模传播及其向高频静电波的转化效应,获得了激发的等离子体波通量.Eliasson等[16]数值计算了不均匀体尺度、电子密度扰动强度等对O模电磁波异常吸收效应影响.Mishin等[17]基于对欧洲非相干散射联合会(Europe Incoherent SCAtter, EISCAT)与美国高频主动极光研究项目(High Frequency Active Auroral Research Program,HAARP)实验中激发的等离子体湍流与下降“电离”层的特征分析,研究得出在加热频率远离电子回旋谐波频率时异常吸收效应减弱,并在上混杂共振区域同样产生强朗缪尔湍流.
本文研究第二种类型的由热参量不稳定性引起的异常吸收效应,在Graham等[10]等理论研究的基础上,采用动理论方法,结合磁化等离子体中电波色散关系和地磁场中电子运动引起的高频电导率的变化等,详细推导出更精确的O模电磁波异常吸收系数的表达式.模拟计算了异常吸收系数随地磁倾角的变化,并与文献[10]结果进行了比较.
1 磁化等离子体中异常吸收系数
1.1泵波电场作用下等离子体中的位移电流
当等离子体处于恒定外磁场B0中时,考虑在外加泵波电场E0eiω0t驱动下等离子体中的纵向振荡,ω0为泵波角频率.电离层中离子被认为是一组随机分布的离散点电荷,由于本文研究的异常吸收效应主要针对高电离层加热,与低电离层欧姆加热不同,在高电离层中电子碰撞频率相对较低,因此,电子的动力学过程可用无碰撞的弗拉索夫方程[18]描述,有
(1)
式中:F(r,v,t′)为位置为r、速度为v的电子在t′时刻的分布函数;Φ(r,t′)为电势,振荡电场Es=-Φ;e和me分别为电子的电荷和质量.对方程(1)作如下变量代换:
ρ=r+ξeiω0t,u=v+(ξ/(iω0))eiω0t,t=t′.
式中:ξ为处于磁场中的电子在驱动电场作用下的电位移矢量,
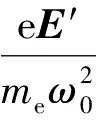
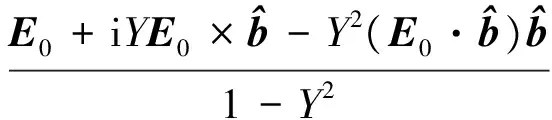
(2)
经过上述变量代换后,方程(1)可以写成
(3)
考虑电子分布函数偏离原平衡态的小扰动,即F=f0+f,Φ=0+φ,其中f0满足麦克斯韦分布,f为分布函数的一阶扰动,φ为电势的一阶扰动.参照Dawson和Oberman[8]处理方法,采用微扰法且仅保留一阶项对方程(3)进行线性化,并引入波矢k对f及φ进行空间傅里叶变换[8],得到如式(4)所示的扰动电势:
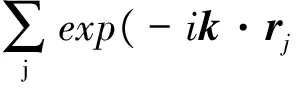
(4)
式中:k为波数,代表波矢的数值;rj表示粒子的位置;ε0为真空中的介电常数;D(k,ω)为等离子体介电函数.
等离子体中的电子和离子对外驱动电场的响应存在显著差异,电子的快速振荡使得慢离子能够“感受到”宏观等效电场,宏观电场Eie可以用扰动电势φk(t)表示:
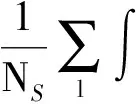
(5)
式中:NS=N0V为散射体积V内总电子数,N0为平均电子密度.散射体内电子密度起伏可写成如下形式:
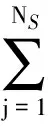
(6)
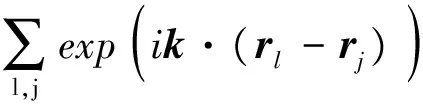
=NS〈exp(ik·(rl-rj))〉
=〈n(k,t+τ),n*(k,t)〉
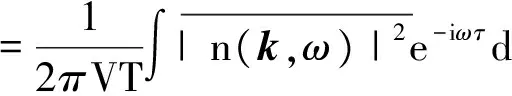
(7)
式中,T为扰动持续时间.
[10],相对等离子体密度起伏功率谱可写为
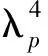
(8)
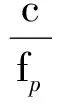

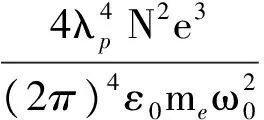
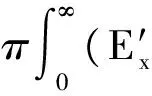
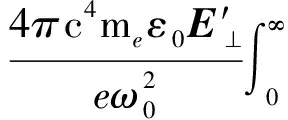
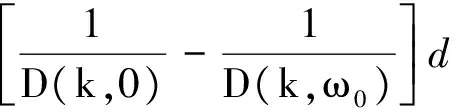
(9)
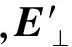
在外磁场中,等效电场力所产生的位移电流为
Jie=-eve
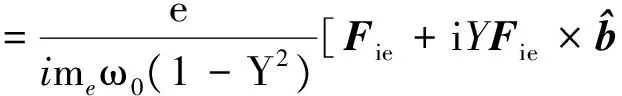
(10)
式中运动速度ve由运动方程确定.将式(9)代入(10),可得
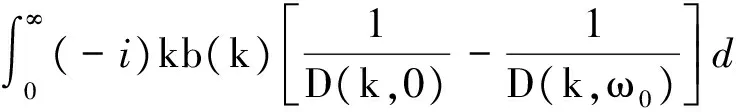
(11)
1.2单位路径上的电波能量损耗
对于外电场,沿波矢量方向的坡印亭矢量可以表示为
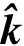
(12)
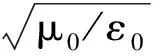
(13)
式中:
F12=(RL-PS)2sin4θ+4P2D2cos2θ,
R=1-X/(1+Y),
L=1-X/(1-Y),
S=(R+L)/2,
D=(R-L)/2,
P=1-X;
A=Ssin2θ+Pcos2θ;
B=RLsin2θ+PS(1+cos2θ);
C=PRL.
利用所建立的坐标系,外电场E0=(E0x,E0y,E0z),假定波矢量和与地磁场的夹角为θ,即k=(ksinθcosφ,ksinθsinφ,kcosθ).在上述坐标系下,电磁波的偏振关系[20]如公式(14)所示:
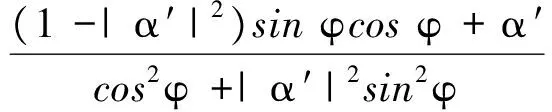
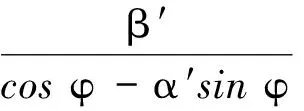
(14)
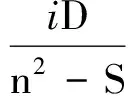
利用式(14)偏振关系,沿波矢方向的电场分量如
(15)
所示.另外,
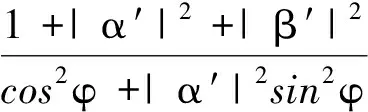
(16)
将式(15)代入式(12),可得沿波矢量方向的平均能流密度为
(17)
将式(16)代入式(17)可得
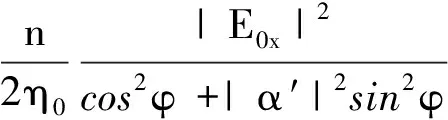
[cos2θ+|α′|2+|β′|2sin2θ-
2|β′|sinθcosθ].
(18)
在磁化等离子体中,等离子体纵向振荡的色散关系[21]可以用公式(19)表示:
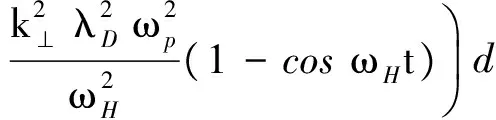
(19)
式中:λD为电子德拜长度;ωp为电离层等离子体共振频率.对于沿垂直于外磁场方向传播的静电上混杂波,色散关系可以近似表示为
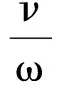
(20)
式中:ν为电子有效碰撞频率;D(k,0)为纯实数,D(k,ω)=Dr(k,ω)+iDi(k,ω).在碰撞频率ν足够低时,色散关系式(20)相当于以kω0为中心的δ函数,kω0为式(21),其中vth为电子热速度,
(21)
将公式(11)中积分项可写成如下的实部和虚部形式:
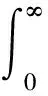
=Ir+iIi.
(22)
由异常吸收所导致的单位体积内的电波能量损耗Qloss可以表示为
Qloss=
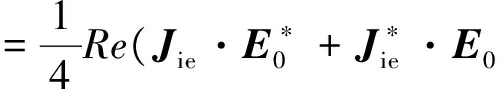
(23)
将位移电流表达式(11)、E0=(E0x,E0y,E0z)的偏振关系式(14)代入公式(23).另外,由于
=|E0x|2(α-α*)
=i2|E0x|2Im(α)
为纯虚数,因此有
[(1+Y2)|E0⊥|2-4Y|E0x|2Im(α)],
又由于Jie*·E0=(Jie·E0*)*,可以得到
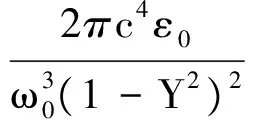
[(1+Y2)|E0⊥|2-4Y|E0x|2Im(α)].
(24)
利用偏振关系式(14),式(24)可以改写为
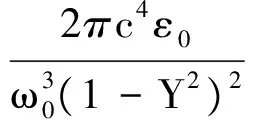
(25)
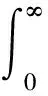
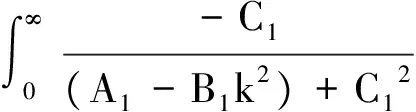
(26)
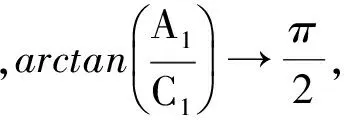

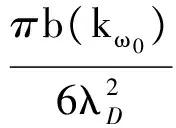
(27)
将式(27)代入式(25),有
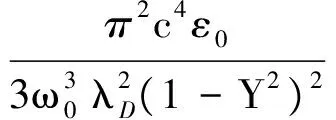
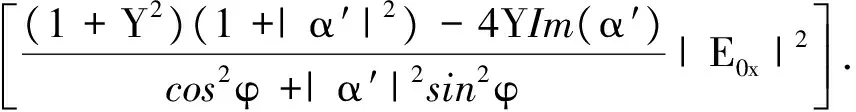
(28)
1.3异常吸收系数
利用式(18)和(28),可以给出单位路径上的损耗
(29)
因此,异常吸收系数为
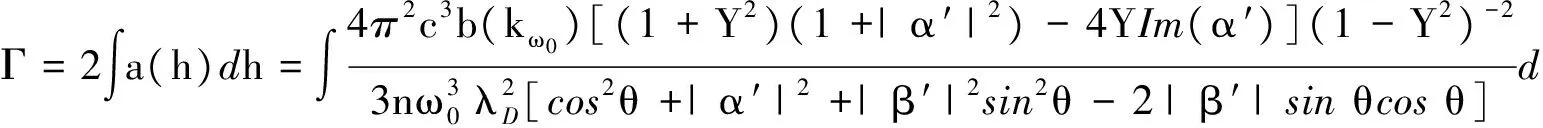
(30)
至此,推导出了磁化等离子体中异常吸收系数表达式,如果将公式中与磁场有关的项Y取为0,则得到与文献[10]相一致的异常吸收系数表达式.
利用式(30)可进一步得到异常吸收系数的解析表达式.根据电离层加热理论,式(30)中积分的贡献主要来自于上混杂共振高度,因此,b(kω0)可以看作是δ函数b(kω0)=b0δ(h-huh).式(30)可写成如下形式:
(31)
式中
(32)
参考文献[9],人工不均匀体密度均方数可以用后向散射系数表示:
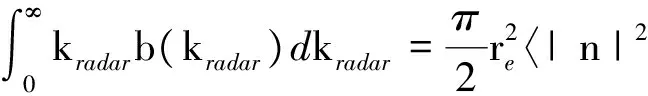
(33)
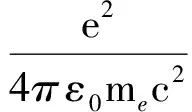
(34)
2 吸收系数随地磁倾角变化
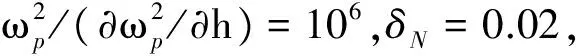
从图1可以看出,本文计算结果与文献[10]具有相同的变化趋势,随着地磁倾角的增加异常吸收系数增大,在地磁倾角约70°后,异常吸收系数略有下降.与文献[10]相比,在考虑地磁场对电子运动影响后,本文计算的异常吸收系数相对偏低,且随着地磁倾角的增加其差值不断增大,最大接近2 dB.
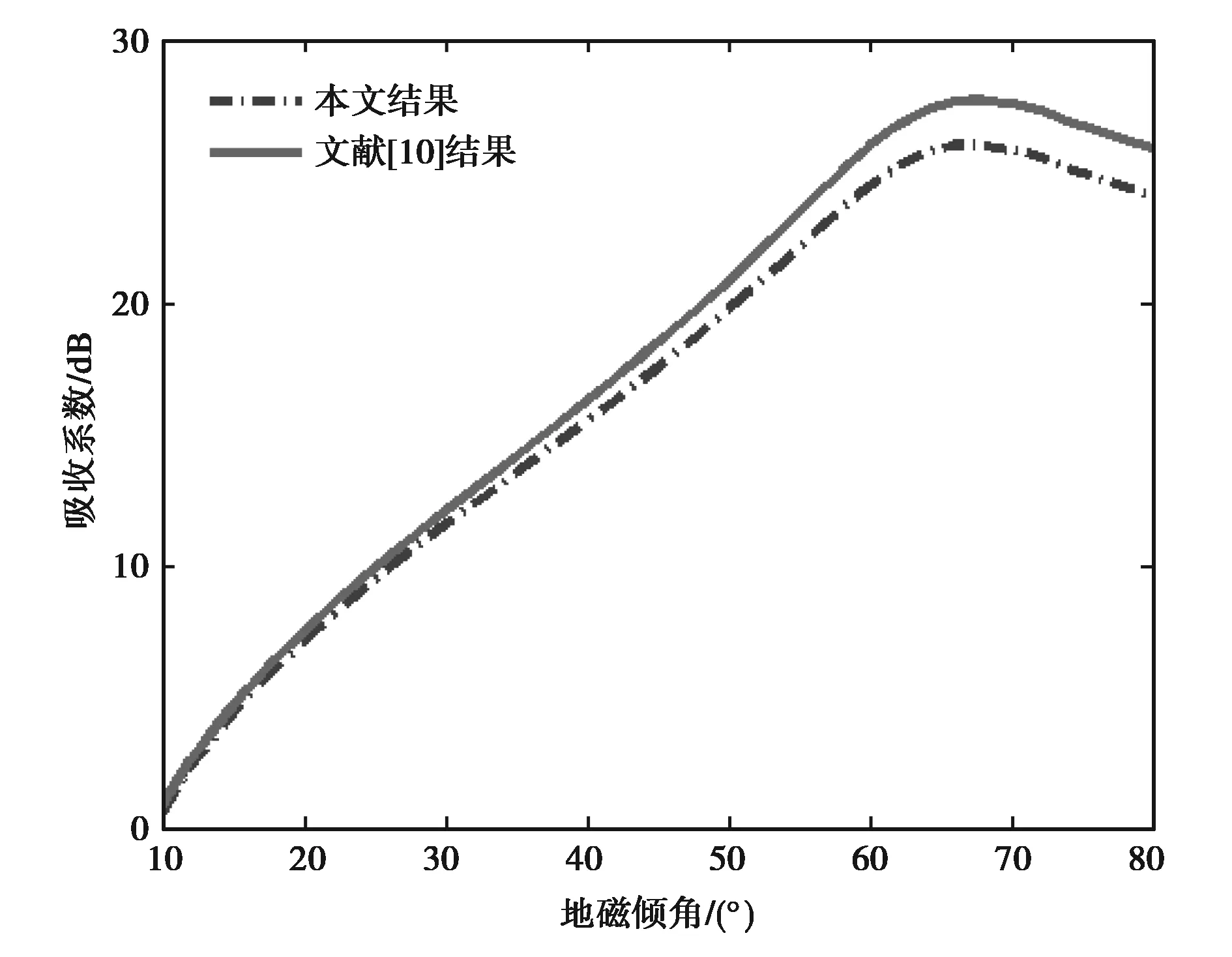
图1 异常吸收系数随地磁倾角的变化
3 结论和讨论
受电离层加热激发人工沿磁场分布不均匀体影响,入射到该区域的大功率高频电波与小功率的高频诊断波经波模转化过程形成上混杂本征波,从而引起电波幅度的异常吸收效应.异常吸收是重要的电离层加热效应之一,直接反映着泵波能量转化效率.在以往异常吸收系数计算中往往忽略了地磁场对电子运动的影响.本文利用动理论方法,从弗拉索夫运动方程出发,考虑磁化等离子体中电波色散关系和泵波电场形成的位移电流,详细推导出更精确的异常吸收系数的表达式.并模拟计算了异常吸收系数随地磁倾角的变化,结果表明随着地磁倾角的增加,异常吸收系数增加,在约70°后缓慢下降.与文献[10]结果比较表明,在考虑了地磁场对电子运动的影响后,异常吸收系数相对降低,且随地磁倾角增大,影响越明显.
本文主要研究O模电磁波异常吸收情形,下一步将开展X模电磁波情况及利用异常吸收反演人工不均匀体尺度的方法研究.
参考文献
[1] 黄文耿, 古士芬, 龚建村. 大功率高频无线电波加热电离层[J]. 电波科学学报, 2004, 19(3):296-301.
HUANG W G, GU S F, GONG J C. Ionospheric heating by powerful high-frequency radio waves[J]. Chinese journal of radio science, 2004, 19(3): 296-301. (in Chinese)
[2] KUO S P. Ionospheric modifications in high frequency heating experiments[J]. Physics of plasmas, 2015, 22:012901. DOI: 10.1063/1.4905519
[3] COHEN R, WHITEHEAD J D. Radio-reflectivity detection of artificial modification of the ionospheric F layer [J]. Journal of geophysical research, 1970, 75(31): 6439-6445.
[4] STUBBE P, KOPKA H, JONES T B, et al. Wide band attenuation of radio waves caused by powerful HF waves: saturation and dependence on ionospheric variability[J]. Journal of geophysical research, 1982, 87(A3): 1551-1555.
[5] STOCKER A J, ROBINSON T R, JONES T B. Observations of the effects of ionospheric heating on the amplitude of low-power diagnostic radio waves at Arecibo[J]. Journal of geophysical research, 1992, 97(A5): 6315-6322.
[6] ERUKHIMOV L M, METELEV S A, MYASNIKOV E N, et al. Artificial ionospheric turbulence [J]. Radiophysics and quantum electronics, 1987, 30(2): 208-225.
[7] DAWSON J, OBERMAN C. High-frequency conductivity and the emission and absorption coefficients of a fully ionized plasma [J]. The physics of fluids, 1962, 5(5): 517-524.
[8] DAWSON J, OBERMAN C. Effect of ion correlations on high-frequency plasma conductivity [J]. The physics of fluids, 1963, 6(3): 394-397.
[9] MINKOFF J. Radio frequency scattering from a heated ionospheric volume, 3, cross section calculations[J]. Radio science, 1974, 9(11): 997-1004.
[10] GRAHAM K N, FEJER J A. Anomalous radio wave absorption due to ionospheric heating effects[J]. Radio science, 1976, 11(12):1057-1063.
[11] ROBINSON T R. The heating of the high latitude ionosphere by high power radio waves[R]. Physics Reports, 1989(2/3): 79-209.
[12] FROLOV V L, CHUGURIN V V, KOMRAKOV G P, et al. Study of large-scale irregularities generated in the ionospheric F-region by high-power HF waves [J]. Radio physics and quantum electronics, 2000, 43(6): 497-519.
[13] ZABOTIN N A, BRONIN A G, ZHBANKOV G A, et al. Anomalous attenuation of extraordinary waves in ionosphere heating experiments [J]. Radio science, 2002, 37(6): 1102.
[14] ZABOTIN N A, WRIGHT J W, KOVALENKO E S. Multiple scattering effects in ionospheric radio sounding [J]. Radio science, 2004, 39: RS002953.
[15] VAS’KOV V V, RYABOVA N A. Anomalous absorption of radiowaves by small-scale cylindrical irregularities stretched along the magnetic field[J]. Plasma physics reports, 2007, 33(10): 850-858.
[16] ELIASSON B, PAPADOPOULOS K. Numerical study of anomalous absorption of O mode waves on magnetic field-aligned striations [J]. Geophysical research letters, 2015, 42: 2603-2611.
[17] MISHIN E, WATKINS B, LEHTINEN N, et al. Artificial ionospheric layers driven by high frequency radiowaves: an assessment[J].Journal of geophysical research: space physics, 2016, 121: 3497-3524.
[18] CLEMMOV P N, DOUGHERTY J P. Electrodynamics of particles and plasmas[M]. Massachusetts: Addison-Wesley, 1969.
[19] STIX T H. The theory of plasma waves[M]. New York: McGraw-Hill, 1962.
[20] AKHIEZER A I. Plasma electrodynamics[M]. Oxford: Pregamon Press, 1975.
[21] BERNSTEIN I B. Waves in plasma in a magnetic field [J]. Physical review, 1958, 109(1):10-21.
满莉(1984—),女,山东人,中国电波传播研究所工程师,硕士,主要研究方向为电离层物理等.
马广林(1984—),男,河南人,中国电波传播研究所工程师,硕士,主要研究方向为电离层加热理论仿真.
车海琴(1982—),女,湖北人,中国电波传播研究所工程师,硕士,主要研究方向为电离层物理、等离子体技术等.
Anomalousabsorptioneffectonmagnetizedplasmainducedbyionosphericmodification
MANLiMAGuanglinCHEHaiqin
(NationalKeyLaboratoryofElectromagneticEnvironment,ChinaResearchInstituteofRadiowavePropagation,Qingdao266107,China)
The amplitude anomalous absorption of an O-mode low-power diagnostic radio wave passing through the perturbed region in ionospheric modification is investigated. Kinetic theory and Vlasov equation describing electron dynamics are employed to derive the coefficient of anomalous absorption caused by artificial field-aligned irregularities, considering effects of a magnetic field on the dispersion relationship of EM waves and on motions of electrons in calculations of the displacement current density. With analytical expressions, variations of the anomalous absorption coefficient with the geomagnetic dip are calculated. It is shown that the coefficient increases with the geomagnetic dip until 70o, and then drops off slowly. With consideration of the geomagnetic field when calculating the HF conductivity, the coefficient is decreased and more obvious at high geomagnetic dip.
ionospheric modification; anomalous absorption; magnetized plasma; Kinetic theory; geomagnetic dip
满莉, 马广林, 车海琴. 磁化电离层等离子体异常吸收效应研究[J]. 电波科学学报,2017,32(4):434-440.
10.13443/j.cjors.2017021301
MAN L, MA G L, CHE H Q. Anomalous absorption effect on magnetized plasma induced by ionospheric modification[J]. Chinese journal of radio science,2017,32(4):434-440. (in Chinese). DOI: 10.13443/j.cjors.2017021301
P352.3
A
1005-0388(2017)04-0434-07
DOI10.13443/j.cjors.2017021301
2017-02-13
中国电科技术创新基金(KJ1602004)
联系人: 满莉 E-mail: manlionly@qq.com

