振动发电机的系统建模与频率特性分析
王志华, 张少鹏, 姚 涛, 吕殿利, 张惠娟
(1.电磁场与电器可靠性省部共建重点实验室,河北工业大学电气工程学院, 天津 300130;2.河北工业大学机械工程学院, 天津 300130)
振动发电机的系统建模与频率特性分析
王志华1, 张少鹏1, 姚 涛2, 吕殿利1, 张惠娟1
(1.电磁场与电器可靠性省部共建重点实验室,河北工业大学电气工程学院, 天津 300130;2.河北工业大学机械工程学院, 天津 300130)
采用两自由度振动模型对振动发电机进行描述,由于非线性磁力的影响,该模型表明电磁式振动发电机是非线性非自治系统。基于该模型,对正弦振动激励下的系统响应进行仿真分析,结果表明,动子与定子的相对位移响应出现了明显的倍频现象,而输出电动势的频率分布更加复杂,不但有对应激励频率的主振动解和亚谐振动解,而且还有对应固有频率的亚谐振动解和超谐振动解,表明系统具有较强的非线性,且随着输入振动能量增大,系统的非线性特征更加明显。在10Hz正弦振动激励下的测试发现,输出电动势的幅频特性在10Hz、20Hz和30Hz处出现峰值,表明输出电动势出现了明显的倍频信号,实验结果与仿真结果的频率特性一致。
两自由度模型; 系统响应; 非线性; 频率特性; 振动发电
1 引言
无线传感器网络、便携式电子设备等发展迅速,而电源有限的容量严重制约了它们的使用寿命。振动能源是环保的可再生能源,在这些电子设备的工作环境中广泛存在,利用永磁振动发电技术为其供电得到国内外研究人员的广泛研究。
拾振效率直接决定了振动发电机的机电转换效率,学者对多种拾振机构形式进行了研究。由于永磁弹簧具有非接触性、适于低至几赫兹的低频振动等优点,在用于人体振动等条件下的振动发电机上得到了应用[1,2]。为了提高拾振机构在微弱激励下的响应振幅,实现双稳态振动,采用变刚度拾振机构,对比单一刚度拾振机构,增大了响应振幅,拓宽了频带,提高了发电功率[3]。
要深入掌握电磁式振动发电机的机电耦合规律,需要对其机电转换规律进行研究。文献[4]对圆柱形电磁式振动发电机进行了数学分析,研究表明磁铁尺寸、气隙、线圈匝数都对其结果有影响。类似结构的圆柱形永磁发电机可以用于波浪发电[5,6]。采用弹簧-质量-阻尼构建振动发电机系统模型,在机电耦合仿真过程中将非线性磁力进行多项式拟合,研究表明该数学模型可以描述电磁式振动发电机的机电转换规律[7]。
为了提高发电效率,感应线圈结构的设计也得到学者的重视。通过在悬臂结构注入多层螺旋线圈可降低振动发电机的固有频率,提高输出功率[8]。
实现电能的高效管理和输出也很重要,这需要在电路元器件的高度集成和低电压电源的电能高效处理等方面进行研究[9-11]。从当前储能技术发展情况来看,一种储能技术很难同时满足这两种需求,需要同时采用多种储能技术,配置多元的储能电源,使其彼此间协调控制、综合规划,最大限度发挥储能电源的效用[12]。如果输出电能较多,可以采用超级电容和蓄电池混合储能技术[13]。在对超级电容充电过程中,为了提高系统的能量转换效率,采用半桥变换器和倍压器组合的电压均衡策略,结果表明,系统的能量转换效率明显提高,大约为90%[14]。在电池管理系统中,利用DC-DC 双向变换电路既可以工作在Buck 模式,也可以工作在Boost 模式,可以实现能量的双向流动用于蓄电池的充放电,以实现蓄电池的储能[15]。
由于实际振动环境的影响,振动发电机输出的电能为非正弦、非周期交流电,除了分析相关电信号的大小等基本参数外,还需要对其频率特性进行研究。由于在计算中需要采用数值分析,分析频率特性时主要采用离散傅里叶变换[16]、周期过零点插值原理等[17]。但是,要想从根本上提升振动发电机的能量转换效率,需要对振动发电机的频率特性进行深入研究。
本文将建立振动发电机的系统模型并对其进行机电耦合特性分析,对动子与定子相对位移、输出电动势等响应进行频率特性分析,同时制作样机进行实验研究。
2 振动发电机数学模型
2.1系统模型
对于电磁式振动发电机动态响应规律的分析需要掌握系统的阻尼、刚度特征,由于运动速度相对较小,认为系统的质量是不变的。下面对电磁式振动发电机的机电耦合模型中的关键问题进行剖析。
直线式电磁式振动发电机不同于传统的直线发电机,振动发电机用于车辆、桥梁等环境时,难以固定在一个静止不动的基础上,而是与用电设备在平台上一起振动,因此,在分析上有着明显不同。
对于直线式电磁式振动发电机,其动子的主要运动方向为轴向,在轴承等限位机构的作用下,其径向运动忽略不计。外界输入振动首先作用在发电机外壳上,然后通过拾振机构将振动能量传递到动子。因此,由等效系统的方法,可采用两自由度振动模型对其进行描述,根据振动发电机结构特征,可以建立相应的两自由度振动系统模型,如图1所示。
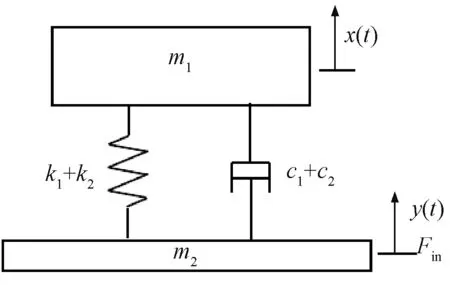
图1 电磁式振动发电机的两自由度模型Fig.1 Two freedom model of permanent magnet vibration-to-electrical generator
图1中,轴向的线性位移为广义坐标,x(t)为动子位移;y(t)为定子和外壳的位移,假设振动平台与外壳之间刚性连接,则振动平台的激励位移也是y(t);质块m1代表动子的质量;m2代表定子和外壳的总质量,这里认为定子和外壳之间刚性连接,具有相同的位移响应规律;动子上下两端均与外壳之间通过弹簧连接,k1和k2为拾振机构的等效弹簧刚度;c1和c2为阻尼系数;Fin为外界施加在外壳上的力。
有学者提出在二语习得中,影响语言迁移的社会因素有很多,主要包括学习者的文化传统、思维模式以及非语言交际等。本文从探讨影响语言迁移的社会因素出发,发现这些因素都会影响母语迁移的发生,这些因素可能对母语迁移产生正迁移,也可能对母语迁移产生负迁移。
当电磁式振动发电机在振动激励下工作时,一般情况下,其外壳受到的位移激励函数更容易确定。因此,这里的外壳和定子可以看作位移函数为y(t)的支撑体[18],则永磁振子会产生一个相应的位移响应x(t)。以动子m1和定子m2的静平衡位置为坐标原点,根据脱离体模型可得:
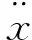
(1)
(2)
式中,Fma为无感应电流影响时定子对动子作用的磁力,与动子和定子的相对位移有关。根据有限元仿真结果,在不考虑感应电流产生磁场的条件下,磁场作用力Fma采用傅里叶级数进行拟合具有较好的精度。
令ceq=c1+c2,keq=k1+k2,则式(1)和式(2)可整理为矩阵形式:
(3)
式中
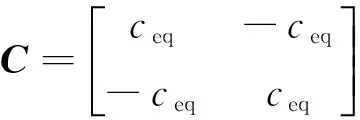
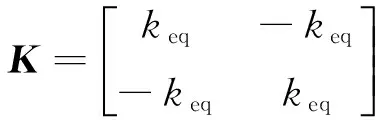
由于不考虑刚度和阻尼的非线性,使得阻尼矩阵和刚度矩阵均为对角矩阵,在求解时微分方程没有耦合问题。
上述系统模型表明,由于非线性磁场作用力的影响,使得电磁式振动发电机为非自治系统,可通过计算动子位移和速度的相轨迹判断系统的稳定性。
在进行感应电动势的计算中,主要考虑感应线圈中磁通的变化率,而磁通的变化率与动子和定子的相对位移变化有关,动子和定子相对位移函数可表示为z(t)=x(t)-y(t)。
根据法拉第电磁感应定律,感应线圈的输出电动势EMF为:
(4)
由式(4)可以看出,提高振动发电机的输出电动势,可通过下面两种方式入手:提高动子与定子的相对运动速度,增加磁链与动子和定子相对位移的变化率。
3 仿真分析
3.1系统稳定性分析
基于第2节理论结果,对一发电机模型进行仿真分析。发电机模型参数为:定子由E型硅钢片叠制而成,动子由圆柱永磁体和圆柱状非导磁材料制成,动子质量m1=0.95kg,定子质量m2=1kg;永磁体的材料为圆柱形钕铁硼,直径20mm,高10mm;弹簧的刚度k=1.5N/mm;动子通过轴承进行限位和润滑,给定轴承的阻尼为10N/(m/s)。基于有限元法计算振动发电机的磁场分布、感应线圈中的磁通和动子定子之间的磁场作用力。
考虑到非正弦的周期激励一般都可以分解为一系列正弦激励的叠加,因此下面对简谐振动下的电磁式振动发电机的振动情况进行分析。给定外界输入振动位移激励为y(t)=10sin(20πt)mm。
从振动发电机静平衡位置开始仿真,对64个激振周期的系统响应进行分析,分别以动子与定子的相对位移和相对速度为横坐标和纵坐标,绘制的相轨迹如图2所示。由图2可以看出,在非线性磁力的作用下,系统响应存在多周期的运动状态,但这些周期解均是稳定的。
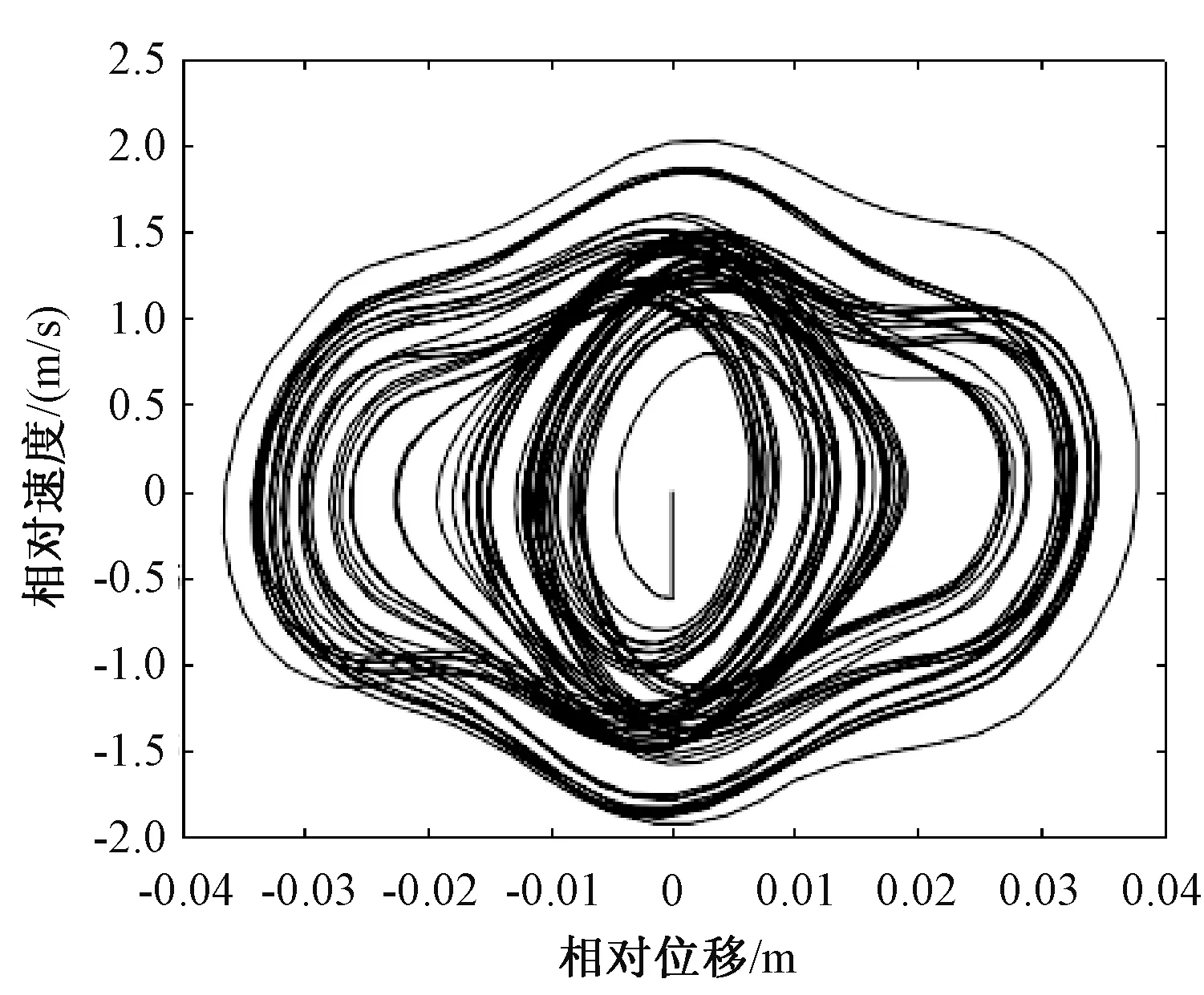
图2 动子与定子相对位移和相对速度的相轨迹曲线Fig.2 Phase trajectory curve about relative displacement and relative velocity of mover and stator
3.2频率特性分析
若位移振动的振幅设定为10mm,在激振频率为6Hz时,动子与定子的相对位移幅频特性曲线如图3(a)所示,发电机的输出电动势幅频特性曲线如图3(b)所示。
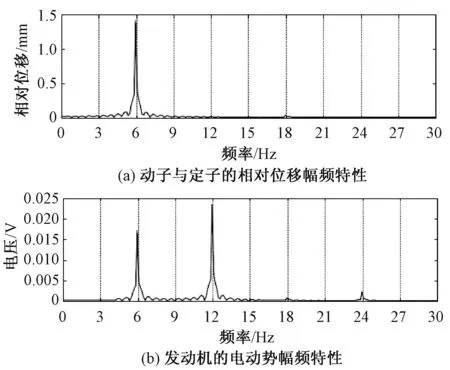
图3 6Hz时的相对位移和电动势幅频特性曲线Fig.3 Amplitude-frequency characteristic curve of relative displacement and EMF at 6Hz
图3(a)表明,由于激振频率与发电机的固有频率一致,因此动子与动子的相对位移频率均集中在6Hz。图3(b)的发电机输出电压则出现了明显的倍频现象,在6Hz和12Hz有两个较大的峰值点,3倍频之后的峰值点体现得不明显,说明经过振动发电机非线性系统的传递,系统的输出电压响应会含有明显的谐波分量。
在激振频率为10Hz时,动子与定子的相对位移幅频特性曲线如图4(a)所示,发电机的输出电动势幅频特性曲线如图4(b)所示。
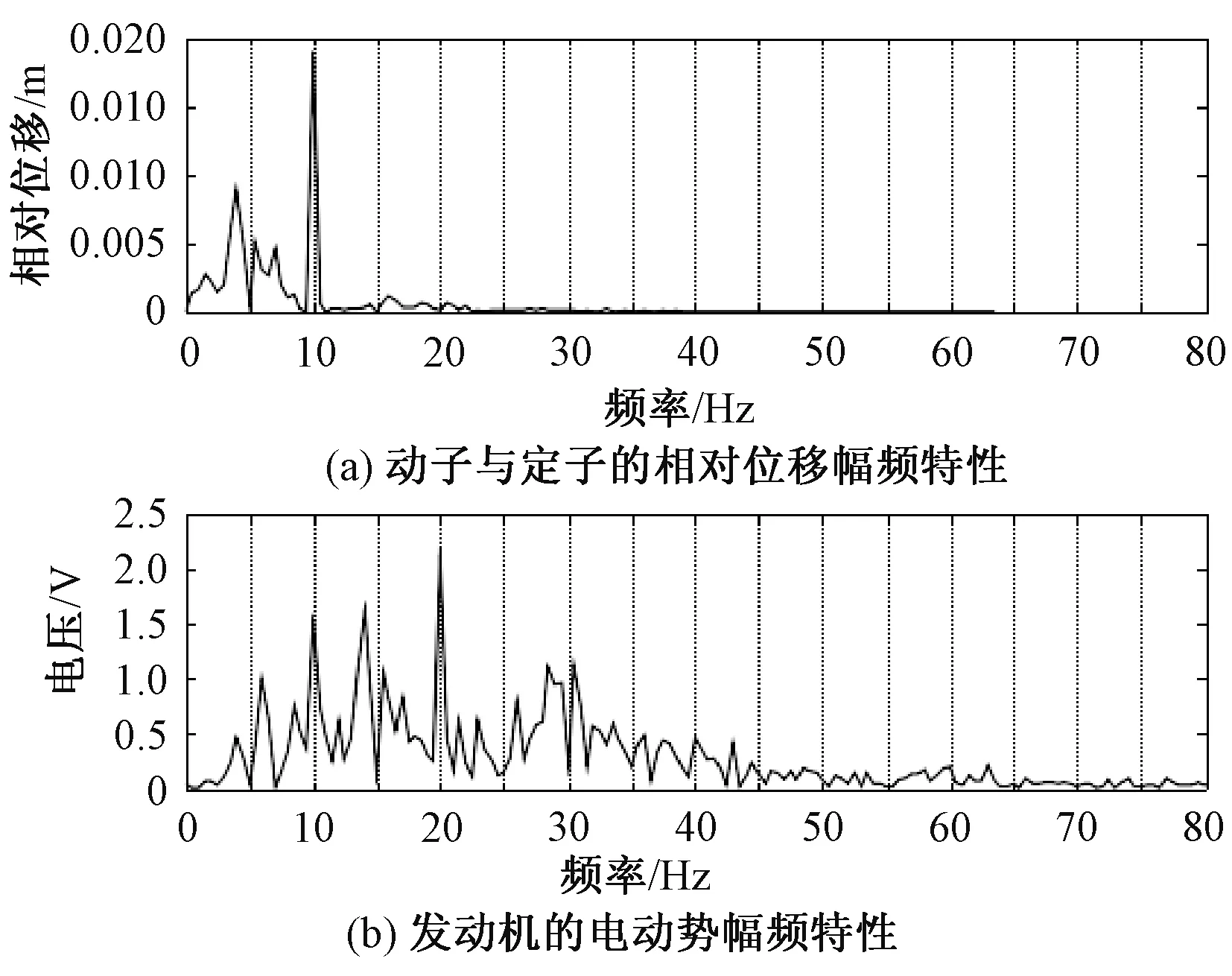
图4 10Hz时的相对位移和电动势幅频特性曲线Fig.4 Amplitude-frequency characteristic curve of relative displacement and EMF at 10Hz
由图4(a)可以看出,动子与定子的相对位移在10Hz出现最大峰值点,该频率与激振频率一致;而在4Hz出现第二大峰值点,且幅频特性在5Hz附近呈现带状分布,表明系统在此情况下出现明显的非线性特征,响应出现了多周期现象。图4(b)几个较大的峰值点依次出现在20Hz、14Hz、10Hz、6Hz、30Hz等,表明非线性磁场力的作用,使得系统在非线性强迫振动条件下不仅出现了与激励频率接近的主振动解和亚谐振动解,而且还有与固有频率接近的亚谐振动解和超谐振动解。
对比图3和图4可以发现,当激振频率较高时,输入振动能量增大,动子与定子的相对位移响应明显增大,磁力的非线性作用变得愈加明显,使系统出现明显的非线性非自治特征。但是,激振频率的增大使得系统的输出电能和效率得到明显提升,因此,考虑到实际的振动环境均为非固定频率的特征,理想意义上的共振状态难以实现,在设计电磁式振动发电机时应综合考虑系统的机电耦合规律,提高输出电能和发电效率。
4 实验研究
课题组制作了振动发电机进行测试,其磁轭采用硅钢片叠压而成,设计过程考虑到了硅钢片的饱和磁感应强度值。采用厚度为5mm的长方体永磁体。将振动发电机固定在电动式振动台上,动子采用轴承进行限位和润滑,动子上下两端均通过弹簧与上下端盖连接。线圈由漆包线绕制,共800匝。
在正弦位移振动激励下对振动发电机进行了测试,由于振动台的限制,在实验中振幅达不到10mm,实验中采用的振动频率和幅值分别为10Hz和4mm。输出电动势如图5所示。
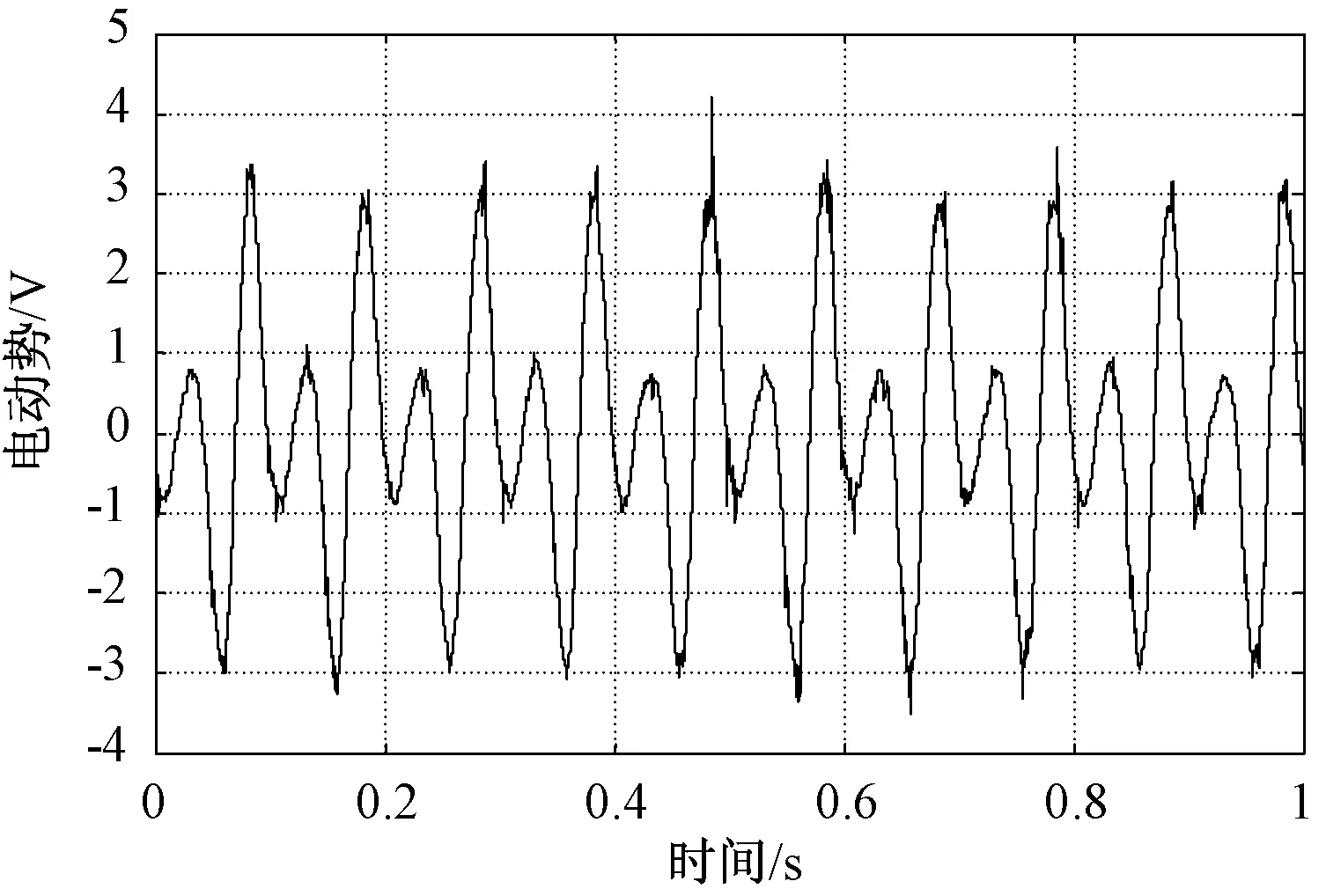
图5 正弦振动激励下的输出电动势实验结果Fig.5 Experimental result of output EMF on condition of sinusoidal vibration
图5中,所测得的发电机输出电动势的均方根值和峰峰值分别为1.60V和7.73V。输出电动势的波形出现了谐波信号。对该电动势进行傅立叶分析,得到的输出电动势的幅频特性曲线如图6所示。
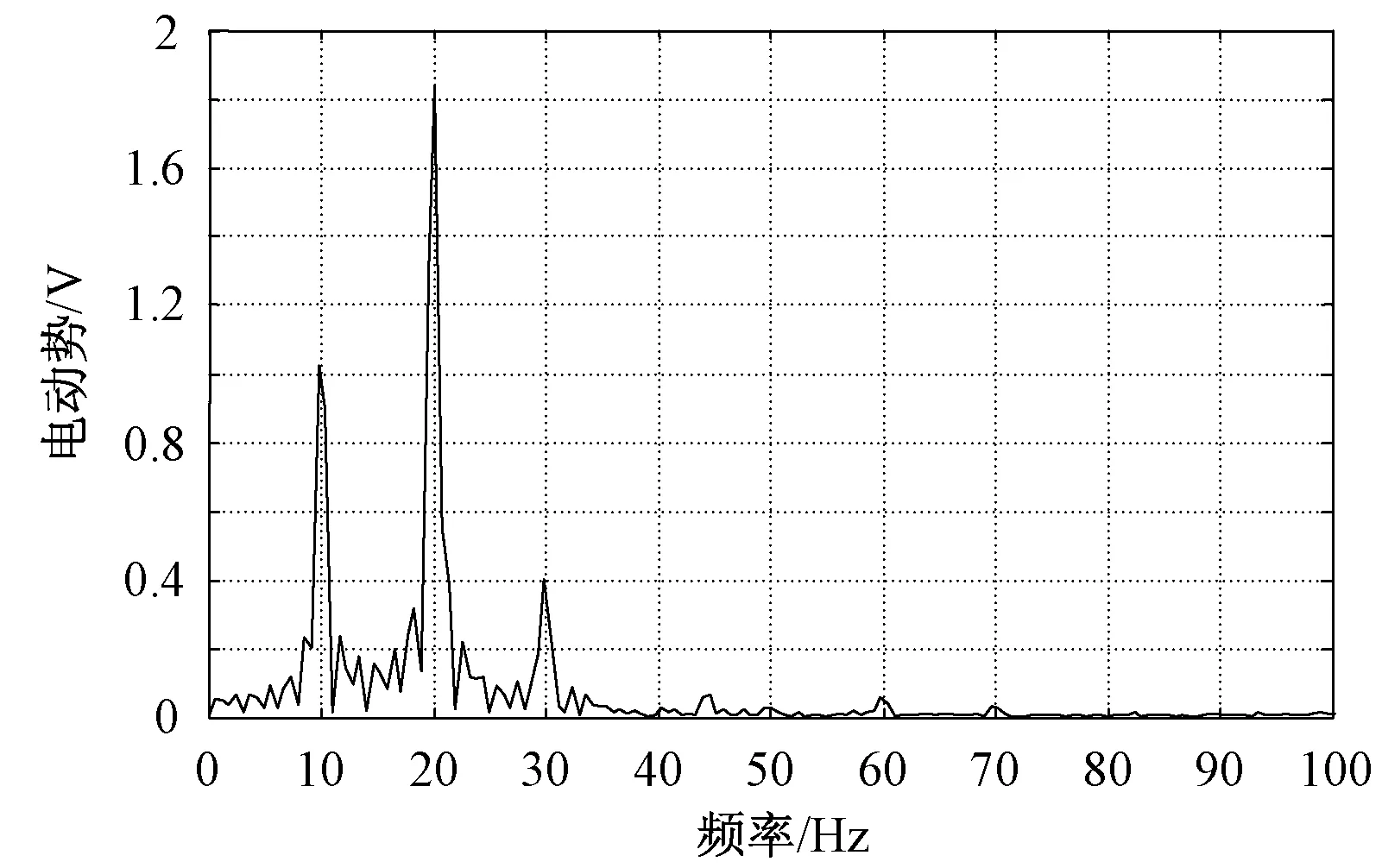
图6 输出电动势的幅频特性曲线Fig.6 Amplitude-frequency characteristic curve of EMF
由图6可以看出,输出电压在10Hz、20Hz和30Hz处出现了明显的峰值,表明输出电动势出现了明显的倍频信号,这与图3(b)和图4(b)的仿真结果具有类似的规律。但是,图4(b)所描述的电动势的信号更加复杂,不但有输入振动对应的倍频信号,还有固有频率对应的倍频信号。对比实验结果和仿真结果,当增大振动频率或振动幅值,使得动子与定子的相对位移较大时,磁力的非线性作用越明显,输出电动势中的谐波信号也愈加繁杂。
5 结论
对于电磁式振动发电机,构建了两自由度振动模型对其进行描述,由于磁力的非线性,使得系统表现出明显的非线性非自治特征。输出电动势与动子定子的相对运动速度成正比,与磁链和动子定子相对位移的变化率成正比。计算结果表明,非线性磁力的作用使得系统始终处于非线性强迫振动条件下,当动子与定子相对位移响应增大时,输出电动势中出现了主振动解、亚谐振动解等多周期信号。通过计算相轨迹,表明系统是稳定的。实验测试表明,在振动频率和幅值分别为10Hz和4mm的正弦振动激励下,输出电动势中有明显的倍频信号,与计算结果规律一致。
[ 1] Liu H C, Gudla S, Hassani F A, et al. Investigation of the nonlinear electromagnetic energy harvesters from hand shaking[J].IEEE Sensors Journal, 2015, 15(2):2356-2364.
[ 2] Zhang Q, Wang Y, Kim E S. Electromagnetic energy harvester with flexible coils and magnetic spring for 1~10Hz Resonance [J]. Journal of Microelectromechanical Systems, 2015, 24(4): 1193-1206.
[ 3] 朱沛, 梁义维, 赵利平(Zhu Pei,Liang Yiwei,Zhao Liping). 变刚度双稳态电磁式振动发电机的AMESim仿真分析(A Simulation and analysis of variable stiffness bistable electromagnetic vibration generator using AMESim)[J]. 微特电机(Small & Special Electrical Machines), 2013, 41(4):21-23.
[ 4] Morgado M L, Morgado L F, Morais N S R. Mathematical modelling of cylindrical electromagnetic vibration energy harvesters[J]. International Journal of Computer Mathematics, 2015, 92(1):101-109.
[ 5] 张静, 余海涛, 陈琦, 等(Zhang Jing, Yu Haitao, Chen Qi, et al.).一种海浪发电用永磁单相直线电机的工作特性与实验分析(Dynamic characteristics and experiment analysis of a single phase permanent magnet linear generator for wave energy conversion)[J]. 电工技术学报(Transactions of China Electrotechnical Society), 2013, 28(7):110-116.
[ 6] 黄磊, 胡敏强, 余海涛, 等(Huang Lei, Hu Minqiang, Yu Haitao, et al.).直驱式波浪发电用全超导初级励磁直线发电机的设计与分析(Design and analysis of a fully-superconducting primary-excitation linear generator for direct-driven wave energy generation)[J].电工技术学报(Transactions of China Electrotechnical Society), 2015, 30(2):80-86.
[ 7] 李恒, 王志华, 姚涛, 等(Li Heng,Wang Zhihua,Yao Tao, et al.).永磁振动发电机的机电耦合分析与实验研究(Electromechanical coupling analysis and experimental study of permanent magnet vibration-to-electrical generator)[J].微电机(Micromotors), 2015, 48(11):18-20.
[ 8] Chen S J, Feng Y Y, Liu S Y. Fabrication of a three dimensional cantilevered vibrational energy harvester using silver ink[A]. 2015 28th IEEE International Conference on Micro Electro Mechanical Systems (MEMS)[C]. 2015. 1075-1077.
[ 9] Liu H, Ji Z, Chen T, et al. An intermittent self-powered energy harvesting system from low-frequency hand shaking[J]. IEEE Sensors Journal, 2015, 15(9): 4782-4790.
[10] Ulus H, Gharehbaghi K, Zorlu O, el al. A fully integrated and battery-free interface for low-voltage electromagnetic energy harvesters[J]. IEEE Transactions on Power Electronics, 2015, 30(5): 3712-3719.
[11] 王志华, 李雨婷, 王莉, 等(Wang Zhihua, Li Yuting, Wang Li, et al.). 基于永磁振动发电的微功耗电能处理电路(A micro power consumption circuit based on permanent magnet vibration generator)[J]. 电工技术学报(Transactions of China Electrotechnical Society), 2015, 30(10): 39-43.
[12] 丛晶, 宋坤, 鲁海威,等(Cong Jing,Song Kun,Lu Haiwei, et al.). 新能源电力系统中的储能技术研究综述(Review of energy storage technology for new energy power system)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2014, 33(3): 53-59.
[13] 杨珺, 张建成, 周阳, 等(Yang Jun, Zhang Jiancheng, Zhou Yang, et al.).针对独立风光发电中混合储能容量优化配置研究(Research on capacity optimization of hybrid energy storage system in stand-alone wind/PV power generation system)[J]. 电力系统保护与控制(Power System Protection and Control), 2013, 41(4):38-44.
[14] 雷加智, 王珂, 成燕,等(Lei Jiazhi, Wang Ke, Cheng Yan, et al.). 一种蓄电池充电器的数字控制器优化设计(Digital controller designing and optimization based on new battery charger)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2014, 33(11):29-34.
[15] 汪玉凤, 周宏胭, 颜廷武,等(Wang Yufeng, Zhou Hongyan, Yan Tingwu, et al.). 基于半桥变换器和倍压器的超级电容均压策略(Voltage balancing strategy based on half-bridge inverter and voltage multiplier for supercapacitor)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2015, 34(1):17-22.
[16] 徐岩, 张晓明, 王瑜, 等(Xu Yan, Zhang Xiaoming, Wang Yu, et al.). 基于离散傅里叶变换的频谱分析新方法(A new method of spectrum analysis based on DFT)[J].电力系统保护与控制(Power System Protection and Control), 2011, 39(11):38-43.
[17] 肖朵艳, 谭卫斌, 张维(Xiao Duoyan, Tan Weibin, Zhang Wei).一种实用的电力系统频率实时测量方法(A practical method of real-time measurement for power system frequency)[J].电力系统保护与控制(Power System Protection and Control), 2014, 42(21):29-33.
[18] Kelly S G. Schaum’s outline of mechanical vibrations[M]. Business Expert Press, 2013.
Systemmodelingandfrequencycharacteristicsanalysisofvibration-to-electricalgenerator
WANG Zhi-hua1, ZHANG Shao-peng1, YAO Tao2, LV Dian-li1, ZHANG Hui-juan1
(1.Province-Ministry Joint Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability, Hebei University of Technology, Tianjin 300130, China; 2.School of Mechanical Engineering, Hebei University of Technology, Tianjin 300130, China)
A vibration model of two degrees of freedom is built for the vibration-to-electrical generator. The model shows that the generator is a nonlinear and non-autonomous system due to the nonlinear magnetic force. The system responses generated by sinusoidal vibrations are calculated on the basis of the model proposed above. The relative displacements between the mover and the stator have obvious frequency multiplication. On the other hand,the system has strong nonlinearity, because the output electromotive force (EMF) contains not only solutions to the main and sub-harmonic vibrations that correspond to vibration frequency, but also the sub-harmonic and the super harmonic vibration solutions that correspond to the nature frequency of the generator. The system will be more nonlinear with more vibration energy input. The tested results show that the amplitude-frequency characteristic of output EMF has obvious peak value at 10Hz, 20Hz and 30Hz under the 10Hz sinusoidal vibration. The output EMF has obvious frequency multiplication which is consistent with the calculated results.
two degrees of freedom model; system response; nonlinearity; frequency characteristics; vibration-to-electrical generator
2016-09-08
国家自然科学基金项目(51107030)、河北省自然科学基金项目(E2012202070)、国家留学基金项目(201506705007)
王志华(1982-), 男, 河南籍, 副教授, 博士, 研究方向为新能源发电技术、新型智能磁器件;
张少鹏(1990-), 男, 河北籍, 硕士研究生, 研究方向为新能源发电。
10.12067/ATEEE1609018
1003-3076(2017)11-0057-06
TM313

