穿新靴，走老路——谈数学高考题

申学勤 刘晓东 李 霞 翟金祥

(贵州省务川中学，贵州 遵义 564300)

穿新靴，走老路
——谈数学高考题

申学勤 刘晓东 李 霞 翟金祥

(贵州省务川中学，贵州 遵义 564300)

每年高考题都会出现一些新鲜、别致，有创新感的题.考生对这部分题感到束手无策，本文就这部分题进行了剖析，并指明了解题思路以及涉及的知识点.

穿新靴走老路；高考题

常言道：穿新靴，走老路是用来形容用旧办法、老套路去应对面临的新事物、新情况.靴是新的，代表人是新时代的人，路是老的，代表依然用旧的思想和办法去解决新问题.

我们以例子来加以剖析：

例1 在测量某物理量的过程中，因仪器和观察的误差，使得n次测量分别得到a1,a2,a3…,an共n个数据，我们规定所测量物理量的“最佳近似值”a是这样一个量，与各数据的差的平方和最小.依次规定，从a1,a2,a3…,an推出的a=____.

解说背景是测量学中的最佳近似值问题，既陌生又新颖，但实质上是常见的二次函数的最值问题，于新颖中见应用，用心良苦.此题的文字叙述，许多考生觉得难以理解，造成了普遍的失分.题目的一个目的就是考“阅读理解”，而认真理解题意，无非是初中的二次函数问题.

例2 是否存在常数a,b,c使得等式：

解说把一个新的情景纳入到“数学归纳法证题”的常规题，实质上是考数学归纳法，但“含而不露”.

例3 某班试用电子投票系统选举班干部候选人，全班k名同学都有选举权和被选举权.他们的编号分别为1,2，3…,k，同意的按“1”，不同意(含弃权)的按“0”.

A.a11+a12+…+a1k+a21+a22+…+a2k

B.a11+a21+…+ak1+a12+a22+…+ak2

C.a11a12+a21a22+···+ak1ak2

D.a11a21+a12a22+···+a1ka2k

解说本题具有高等数学知识背景，对于高中学生来说是新概念、新符号.但实际上为集合中“且”的概念.此高考题是所谓“高观点试题”就是具有高等数学知识背景的试题，主要表现为：或以新符号、新概念出现或以高等数学的概念、定理为依托.新符号如aij(i、j∈N*),新概念如函数的凹凸性，一致连续等符号

ai1,aj2(i=1,2,3……k,j=1,2,3…..k)作为元素可构成一个矩阵：

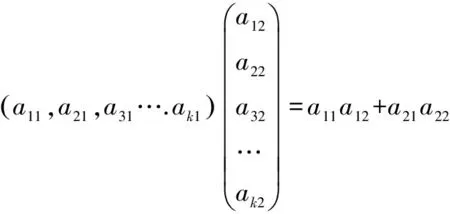
fλx1+1-λx2λf(x1)+1-λf(x2)

例4 如图所示，fi(x)(i=1,2,3,4)是定义在0,1上的四个函数.其中满足性质：“对0,1中任意的x1和x2，任意λ∈0,1，

A.f1(x)、f3(x) B.f2(x)

C.f2(x)、f3(x) D.f4(x)

解说打破常规思维，依题意，从左到右旋转每个号码至少要经过的步数分别为4、5、1、2、1，根据加法原理至少要4+5+1+1+2+1=14步.

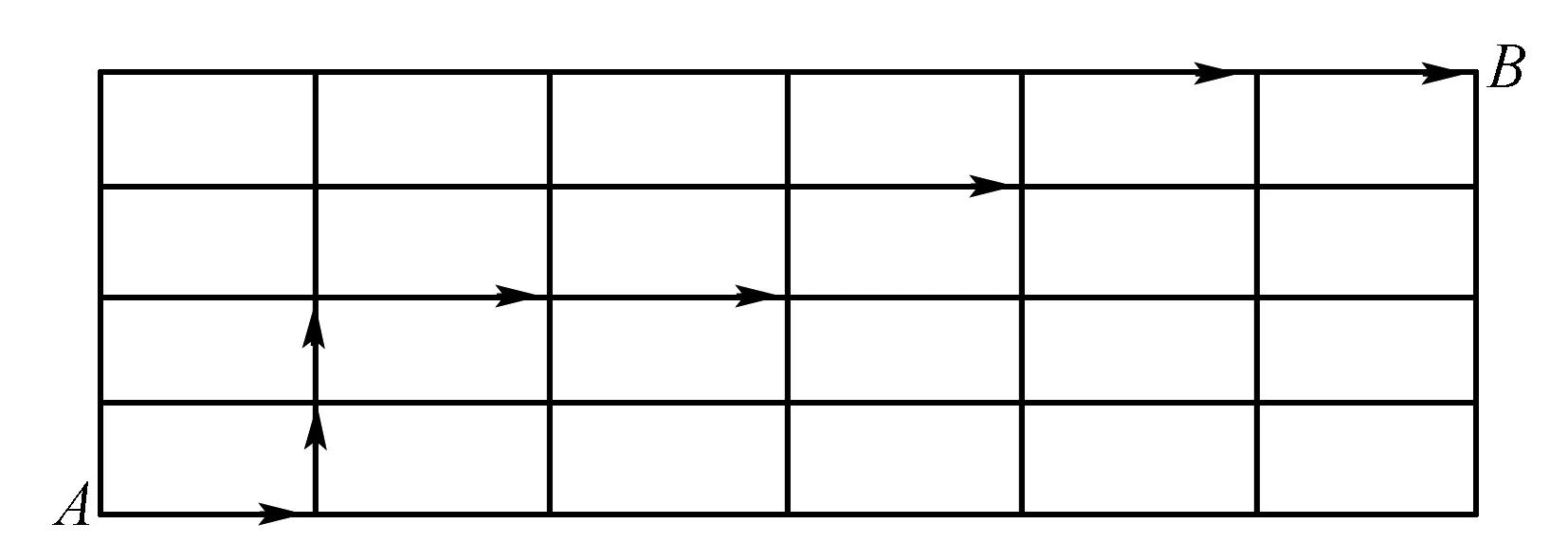
例7 如图，从A到B的路线(规定向上、向右)有多少？

(0重复了4次，1重复了6次)

例11 深夜，一辆马车被牵涉进一起交通事故.该城市有两家马车公司——蓝色和绿色.其中，绿色马车和蓝色马车公司分别占整个城市马车的85%和15%.据现场目击证人说，事故现场的马车是蓝色，现对证人的辨别能力作了测试，测试他的正确辨认率是80%，于是警察就认定蓝色马车具有较大的肇事嫌疑.由于证人的话具有较高的正确辨认能力，因此证人的话具有较大的可信度，试问警察的想法正确吗？

解说本题是概率问题，我们假设该城市共有1000辆马车，那么根据已知信息可得

蓝色：1000*15%*80%=120 绿色：1000*85%*20%=170

例12 (俄国大文豪托尔斯泰的一篇短篇小说《人需要很多土地吗？》)有一个人要卖地，他规定太阳一出来，来买地的人就可以开始跑，一天内跑路圈出来多大地方，这块地就属于他，价格是一千卢布，但太阳落山时必须回到出发地，否则一千卢布就白花了.

有一个叫巴霍姆的人去买地，太阳一出来他就开始跑，他先向前跑了十俄里，才开始向左直弯拐去，又跑了许多路，再向左拐第二个直弯，此时正值中午，烈日当空，饥渴难忍，巴霍姆又跑了两俄里，还有十五俄里赶近路，终于太阳落山时，回到了出发地，但随即倒地不省人事，当家人告诉他圈出的地方不值一千卢布时，巴霍姆立刻口吐鲜血而亡.

解说我们按小说的描述可以画出巴霍姆的路线图，通过案例分析，学生自然而然提出了“最佳路线”问题，即跑同样的路什么时候圈出的地面积最大？并提炼出下面的数学模型：设周长为L的单纯闭曲线C，C为何形状时面积最大，并证明你的结论？

讲解时，一开始学生感到茫然，为了引起学生兴趣，激发学生研究问题的欲望，我们可以创设“小步距”问题情境.

这里涉及两个问题：(1)周长L为定值的n边形中，以正n边形面积最大；(2)周长L为定值的单纯闭曲线中，以圆面积最大.这是从生活中的数学问题谈起，感受数学，沟通主观，数学与社会、周边生活的密切联系.

在上述的例子中我们就实际例题对数学文化的应用，矩阵思想和高中集合交集问题的结合，琴生不等式及拉格朗日中值定理在中学函数中的应用，排列组合思想，笛卡尔直角坐标系的应用，线性规划，概率思想的实际应用等方面作出了分析.由此可见，高中数学不再是简单的计算问题，更多的是实际应用问题，考察学生的综合能力，这与各地纷纷研究新课程改革不谋而合，而高考最根本的目的还是为高校选取真正适合自己的人才.

[1]人民教育出版社,课程教材研究所,中学数学课程教材研究开发中心. 普通高中课程标准实验教科书:数学必修[M]. 北京:人民教育出版社,2011.

[责任编辑：杨惠民]

2017-07-01

申学勤(1961-)，男，贵州省遵义人，本科，中学高级教师，从事高中数学教育与教学.

刘晓东(1976-)，男，贵州省人，本科，中学一级教师，从事高中数学教育教学.

李 霞(1973-)，女，贵州省人，本科，中学一级教师，从事高中数学教育教学.

翟金祥(1990-)，男，江苏省泰州人，本科，中学二级教师，从事高中数学教育教学.

G632

A

1008-0333(2017)28-0038-02