浅析导数定义及其运用

马晓杰

(山东省枣庄市第三中学,山东 枣庄 277102)

浅析导数定义及其运用

马晓杰

(山东省枣庄市第三中学,山东 枣庄 277102)

导数是高中阶段必学的数学知识之一，同样的也是高中数学学习中最难以理解和运用的知识点，至少对于笔者来说，导数的定义及导数运用是很难的.在第一次接触导数时，唯一能够掌握的是简单的运算，但是对于导数的定义是什么却难以理解，直到结合函数与几何知识后才明白了导数的含义，但实际运用中还是很难全面掌握.所以本文将对导数的定义及运用进行分析，希望能够为后来的学习者提供一些帮助.

导数定义；运动几何； 函数

前言导数的定义是导数学习的基础，但实际上高中阶段学生对导数定义很难做到真正理解.在我们学习过程中，老师都会先对导数的定义进行讲解，列举各种函数及其图象来帮助我们理解导数的含义，不过由于函数与导数的复杂性联系，有时候很难分辨清各种函数导数的不同，从而使概念复杂化.还有就是基本导数的运算并不难，但是运用就不简单，虽然能够根据题目列式分析，但实际运用却并不明白.本文是笔者鉴于自己学习导数的一些体会，结合他人对导数的定义及运用的看法，对导数定义及运用的一些个人见解，希望能对高中的同学们在学习导数这个知识时能有一点启发.

一、导数的定义

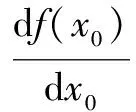
二、导数的运用

1.求函数斜率

就导函数的定义来看的，最基本的运用大概就是求函数在某一点处切线的斜率了，

分析要解题就要明白函数y=f(x)在(1，f(1))的斜率是指f′(1)，这样才能够解题，根据导函数的定义化解式子后，再代入就可以求解出函数在(1,f(1))处切线的斜率是1/2.

这类运用根据的是导数几何定义，这类运用在导数的基础学习中是比较常见的，不过并不是导数常见的运用，这种运用是基本的，难易程度应该是比较简单的.此外，还有用导数定义来求导的计算，这类计算虽然与斜率无关，不过也是比较简单的运用，有些导数的计算如果运用计算公式的话比较复杂，这时候利用定义计算的话就比较便利了.

2.在物理学中的运用

导数除了在数学的基本计算以外，还与物理学相关.

对于非均匀物体来说，质量对长度的导数为物体的线密度.可以说导数的定义对于物理学中的概念有很大的帮助，不仅能够加强对定义的理解，也能够便于计算.

3.求极限

这个可能会比较难以明白，导数的定义就是由极限来的，却又用来求极限，这主要是根据函数求导的限制来进行的.利用的是函数在某点可导与函数在某个领域内可导，及函数可导与不可导之间的关系，通过函数在某点可导的条件，对极限进行求解.

综上所述，导数的定义分为两类，求导过程大体上可以看成是求极限的过程，函数求导要注意定义域及其是否可导.导数定义的运用分为三个部分，除却在数学领域的运用，还有其在物理方面的运用，对于物理方面，指的是导数的物理意义，就像位移的导数是瞬间速度一样；对于数学方面的运用，基本是在求极限及求斜率方面，求斜率是导数的几何定义的运用；对于求极限，是其本质定义的运用.

[1]李庆娟.浅谈导数定义的应用[J].高校讲坛，2012.

[2]施荣权，孙红明.浅谈导数定义及其应用[J].河北能源职业技术学院学报，2015.

[责任编辑：杨惠民]

2017-07-01

马晓杰(2000-)，女，山东枣庄人，枣庄市第三中学2015级29班，在读生.

G632

A

1008-0333(2017)28-0003-02