三维位势问题Legendre级数基本解误差分析

于春肖， 任翠环， 郝雪景

(燕山大学 理学院 河北 秦皇岛 066004)

DOI: 10.13705/j.issn.1671-6841.2017049

三维位势问题Legendre级数基本解误差分析

于春肖， 任翠环， 郝雪景

(燕山大学 理学院 河北 秦皇岛 066004)

对三维位势及位势梯度Legendre级数基本解进行了研究.利用Legendre函数性质和近远场划分准则，推导出位势及位势梯度基本解的截断误差表达式，并分析了有关截断指标对计算精度和计算效率的影响.

Legendre级数； 基本解； 位势； 位势梯度； 截断误差

DOI: 10.13705/j.issn.1671-6841.2017049

0 引言

边界元法(BEM)是一种有效的工程数值计算方法，具有降维、精度高、灵活和速度快等特点.但因计算过程中形成的线性矩阵方程组的系数矩阵是非对称型满阵，边界元法对大规模的工程问题并不适用.基于BEM的上述问题，很多学者对其进行了深入的研究.文献[1]提出了快速多极展开法(FMM)，此算法是一种快速求解积分方程的算法.之后，文献[2]将FMM广义极小残余法(GMRES)结合边界积分方程，得到快速多极边界元(FM-BEM)，此方法使计算量和存储量降低到O(N)，在很大程度上提高了计算效率，被广泛应用到各个领域.文献[3]将快速多极展开技术用于高阶边界元法，降低了计算量和存储量.文献[4-5]对三维弹塑性摩擦接触多极边界元法进行了研究.并对三维轧制过程，建立了点面摩擦接触模型.近几年来，FM-BEM的应用更加广泛.文献[6]将有限元和FMM-BEM结合，来分析结构声学问题.文献[7]研究了FMM-BEM中基础Laplace方程非负解的存在性.

多极展开法[8]是一种近似方法，展开的阶数越多就越接近真实值.在实际中展开的阶数是有限的，也就是存在项数的截断.误差的估计方法有多种，如文献[9]提出了一种新的估计技巧.而本文依据勒让德函数的相关性质，对三维位势及位势梯度Legendre级数基本解展开的截断误差进行了推导，得出级数展开到p项时的误差估计式，从而得到控制精度的方法.

1 三维位势问题的边界积分方程

设有限域为Ω，其表面边界为Γ.已知位势表面为Γ1，已知位势梯度表面为Γ2，且Γ=Γ1+Γ2，则可得Poisson方程的边界积分方程为

其中：x为源点；y为边界Γ上的任意一点；ci为边界形状系数；式中所用到的基本解为u*(x,y)，

其中：q*(x,y)是u*(x,y)在y点处的外法线方向的导数；R为观测点和源点间的距离；n为边界Γ的外法矢.

位势基本解是1/R的函数.为适合多极展开法，将梯度表示为

(3)

其中：m=1、2、3；∂m表示关于xm的偏导数.

2 位势及位势梯度Legendre级数基本解截断误差

Legendre级数多极展开法是对位势问题基本解中的核函数1/R进行级数展开.其近似程度和展开的项数密切相关，展开的项数越多，就越接近真实值.但展开的项数过多，只是增加计算的时间，对提高精度影响不大，所以展开项数一般截断到某一项p，下面对多极展开中的截断误差进行分析.

2.1 位势基本解截断误差

设O为坐标原点,X(r,θ,φ)为场点,Xi(ρi,αi,βi)为源点，两点的相对距离为r/ρi，两点距离为

cosγ=cosθcosαi+sinθsinαicos(φ-βi).

定理1在极坐标中场点和源点的距离为R，则基本解基于Legendre级数展开的截断误差为

证明由公式(2)，可得

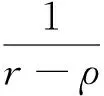
2.2 位势梯度基本解截断误差

定理2若球坐标系下源点为Xi(ρi,αi,βi)，场点为X(r,θ,φ)，且满足cosν=cosθcosα+sinθ·sinαcos(φ-β)，那么

证明要证式(4)，即证[cosθsinαcos(φ-β)-sinθcosα]2≤1-cos2ν.

由夹角间的关系得:

则有[cosθsinαcos(φ-β)-sinθcosα]2+cos2ν=cos2α+sin2αcos2(φ-β)≤1.

定理3若球坐标系下源点为Xi(ρi,αi,βi)，场点为X(r,θ,φ)，且满足cosν=cosθcosα+sinθ·sinαcos(φ-β)，那么

证明要证式(5)，即证1-cos2ν-sin2αsin2(φ-β)≥0.

由夹角间的关系得

定理4球坐标系下，位势梯度的各个分量的截断误差分别为ΔEpr、ΔEpθ、ΔEpφ，则

证明设位势梯度的截断误差为ΔEp，则

由Legendre函数的微商表示与连带的Legendre函数的微商间的关系可得[10]：

根据Legendre函数的正交性及远近场划分准则可得[11]

结合定理2，可得

结合定理3，可得

2.3 位势及位势梯度截断误差分析

由定理1可得三维位势基本解的截断误差式，截断项数p取不同的值时，将Ep*a看作一个整体，其截断误差结果如图1所示.由定理4可得位势梯度的截断误差.截断项数p取不同的值时，将‖ΔEp‖*a2看作一个整体，其截断误差结果如图2所示.

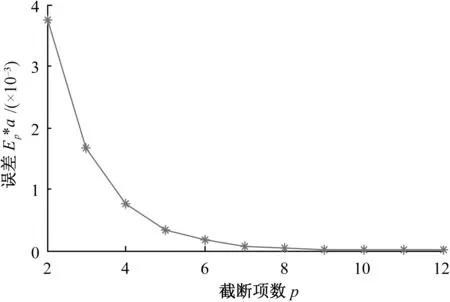
图1 位势的误差 (r/ρ=2)Fig.1 Error for potential

图2 位势梯度的误差(r/ρ=2)Fig.2 Error for potential gradient

从图1和图2中可以看出，当相对距离r/ρ一定时，随着截断项数p的增加，位势和位势梯度的截断误差都在逐渐缩小.

因此，截断项数p对多极展开的计算量、存储量以及求解精度具有重要的影响，适当地选取p值在实际工程计算中尤为重要.由文献[12]知，为了获得一个较高的精度，截断项数p应与log1/2(|)同阶.对于给定的精度要求，就可以用式p=[-log2|]+1([]代表取整),给出其所要求的截断项数.

3 结论

本文从三维位势问题位势基本解入手，对其Legendre级数展开进行详细分析，给出位势及位势梯度Legendre级数基本解的截断误差估计式，并给出一定精度时，截断项数p的选取表达式.研究结果进一步完善了Legendre级数FM-BEM的理论体系，为快速FM-BEM解决位势问题提供了强有力的理论依据.

[1] GREENGARD L，ROKHLIN V．A fast algorithm for particle simulations[J]．Journal of computational physics，1987，73(2)：325-348．

[2] ROKHLIN V．Rapid solution of integral equations of classical potential theory[J]．Journal of computational physics，1985，60(2)：187-207．

[3] 宁德志，滕斌，勾莹．快速多极子展开技术在高阶边界元方法中的实现[J]．计算力学学报，2005，22(6)：700-704．

[4] 刘德义．三维弹塑性摩擦接触多极边界元法和四辊轧机轧制模拟[D]．秦皇岛：燕山大学，2003．

[5] YU C，LIU D，ZHENG Y，et al．3-D rolling processing analysis by fast multipole boundary element method[J]．Engineering analysis with boundary elements，2016，70：72-79．

[6] WU F，LIU G R，LI G Y，et al．A coupled ES-BEM and FM-BEM for structural acoustic problems[J]．Noise control engineering journal，2014，62(4)：196-209．

[7] 李瑞．一类非局部(p,q)-Laplace方程非负解的存在性[J]．郑州大学学报(理学版)，2016，48(2)：5-10．

[8] ROKHLIN L G V．A new version of the fast multipole method for the Laplace equation in three dimensions[J]．Acta numerica，1996，6：229-269．[9] 孙淑珍，石翔宇．抛物型积分微分方程双线性元方法的新估计[J]．郑州大学学报(理学版)，2016，48(4)：6-9．

[10] 刘式适，刘式达．特殊函数[M]．北京：气象出版社，2002：326-361．

[11] SHEN G X，YU C X，LIU D Y．Fast multipole boundary element method in rolling engineering and its research progress[C]//Conference Computational Methods in Engineering. Nanjing，2009:18-20．

[12] GREENGARD L F．The rapid evaluation of potential fields in particle systems[M].Cambridge MA: Mit Press，2003：121-141．

(责任编辑：方惠敏)

ErrorAnalysisofFundamentalSolutionsinLegendreSeriesforThree-dimensionalPotentialProblems

YU Chunxiao, REN Cuihuan, HAO Xuejing

(CollegeofSciences,YanshanUniversity,Qinhuangdao066004,China)

Potential and potential gradient fundamental solutions in Legendre series were studied for three-dimensional potential problems. By using properties of Legendre function and the near-far field partition criterion, truncation error expressions were derived for the potential and potential gradient fundamental solutions. In addition, the influence of truncation index on the computational accuracy and efficiency was analyzed.

Legendre series； fundamental solution； potential； potential gradient； truncation error

2017-03-16

国家自然科学基金项目(11301459)；河北省自然科学基金项目(A2015203121).

于春肖(1977—)，女，河北平山人，教授，主要从事多极边界元法与应用研究，E-mail: chxy@ysu.edu.cn；通信作者：任翠环(1990—)，女，河北衡水人，主要从事多极边界元法及相关算法研究，E-mail: 18713510209@163.com.

O241

A

1671-6841(2017)04-0001-04