基于反预警的反拦截中段规避突防策略

周啟航，刘延芳，＊，齐乃明，闫俊丰，2

基于反预警的反拦截中段规避突防策略

周啟航1，刘延芳1，＊，齐乃明1，闫俊丰1，2

1．哈尔滨工业大学 航天学院，哈尔滨 150006
2．61906部队，廊坊 065000

为了充分挖掘多脉冲机动突防的潜力，提高弹道导弹中段机动突防能力，提出一种基于反预警的反拦截中段规避突防策略。首先，分别以脉冲点火点及点火间隔为搜索节点与步长，视敌方拦截系统为威胁源并转化为航迹规划中的约束条件，将多脉冲弹道的设计问题转化成无人机避障航迹的规划问题。然后，在综合考虑敌方探测系统延迟和拦截系统部署及性能的基础上，选取最优的脉冲点火参数。最后，研究了脉冲增量和探测系统延迟对多脉冲规划的影响。仿真结果表明：所提出的突防策略通过多脉冲机动增加敌方预测误差，使其不能收敛与准确预警，当敌方的预测误差收敛且准确预警时，导弹却处于其拦截范围之外，无法进行拦截；能根据获取的最新战场信息，在线下60s内设计出一条多脉冲突防弹道。此外，还能根据任务的需求，提高（降低）导弹的飞行高度、平均飞行速度，缩短（增加）20%～35%的飞行时间。

弹道导弹；多脉冲；威胁源；避障航迹规划；弹道设计；机动突防

随着导弹突防技术的发展与进步［1－2］，出现了跳跃突防［3］、滑翔弹突防［4］、变射面突防［5］以及多脉冲机动突防［6］等多种中段机动突防策略。多脉冲机动突防能快速地改变导弹的弹道与射程，大幅提高敌方防御系统的探测与拦截难度，有效弥补弹道导弹弹道容易被探测以致被拦截的缺点。相比其他突防策略，多脉冲机动突防对弹头的气动外形、再入角度和防护等要求低且工程上相对容易实现。鉴于此，此项技术受到了国内外学者的广泛关注，并取得了一系列的研究成果。

由于导弹对时间、突防和打击精度的特殊要求，在其他航天器上已经成熟应用的多脉冲变轨原理及方法对其并不适用，在此不再作过多的阐述［7－8］。导弹多脉冲机动突防的关键是在保证导弹能击中目标的前提下选取合适的脉冲点火参数，以使其突防能力最大。文献［9］提出了在弹道最高点通过单脉冲改变导弹射程与剩余飞行时间来进行突防的策略；文献［10］则将其推广到任意点火时刻，并基于遍历法对点火参数进行优化。但文献［9－10］只考虑了单次脉冲作用的情况，且采用的遍历法的计算量很大。文献［11－12］提出了利用多脉冲机动增加敌方预测误差的突防策略，但没有考虑机动后如何保证导弹打击精度的问题。文献［13－15］提出了利用敌方防御系统延迟进行突防的策略，并从同面及异面变轨的角度进行了分析。文献［16］研究了点火时刻对该突防策略的影响，分析了其与导弹射程、飞行时间之间的关系。文献［17］提出了利用拦截器点火空档进行智能规避的策略。但以上多脉冲机动突防策略还存在以下局限性：

1）导弹的突防策略可以分为反探测和反拦截两类。以上突防策略都只是针对其中某一方面，没有将两者综合起来考虑导弹的突防问题，无法充分挖掘多脉冲机动突防的潜力。

2）采用的弹道设计方法必须预先选取中间弹道的落地点，使弹道方程组封闭，但选取规则并没有给出。

3）不能依据战场上敌方防御系统的最新情报信息，快速且有针对性地设计突防弹道。导弹的突防潜力没能完全发挥且打击任务的灵活性不足。

针对以上问题，本文借鉴路径规划中节点搜索及避障规划的思想［18］，结合基于防御系统延迟的突防策略，提出了一种基于反预警的反拦截中段规避突防策略。综合考虑探测系统的延迟与拦截系统的部署、拦截能力，通过“欺骗＋躲避”的方式完成多脉冲机动突防。本文提出的突防策略主要有以下4个创新点：

1）研究导弹突防问题时，综合考虑敌方探测系统的延迟及拦截系统的性能与部署。使导弹具备反预警与反拦截的突防能力，提高其生存概率。

2）将拦截阵地视为障碍物，根据最新情报信息更新其位置、大小及威胁强度，最后将其变成路径规划中的多约束。导弹不是无目的程序式机动，而是有针对性地采用规避策略进行突防，以进一步提高其突防能力。

3）将规避弹道的设计问题转化为避障路径的规划问题，采用路径规划的方法设计弹道，不再需要预先指定中间弹道的落地点。该方法能根据最新的战场信息快速地设计一条突防能力高的弹道，提高导弹作战的灵活性。

4）将三维空间中弹道到拦截阵地的距离问题转换成二维平面内点到椭圆的距离问题，将问题予以简化。

1 多脉冲点火模型

1．1 基本定义

本文将地球视为不转动的匀质球体，采用轨道要素描述弹道。导弹点火时认为其直接获取一个固定幅值的速度增量ΔV，ΔV在弹道面内的投影与导弹速度vi（i＝0，1，…，n）（n为点火次数）的夹角为σi，与弹道平面的夹角为γi，点火点到地心的距离（即点火点的极半径）为ri。

防御系统延迟：导弹防御系统中的探测系统能够准确确定弹道所需的最短时间称为防御系统延迟τ［13］，文献［19］中为4～6min。

基于防御系统延迟的突防策略：导弹飞行过程中，每隔时间Ti（两次点火间隔间导弹的飞行时间）将机动变轨一次，且Ti≤τ。由于防御系统延迟，敌方无法在Ti时间内准确确定导弹的弹道并进行有效的拦截，使导弹突防成功［15］。

如图1（a）所示，定义如下坐标系：

参考坐标系（OXYZ）：以地心O为原点，地心与参考弹道的关机点的连线为Y轴，在参考弹道面内过球心且垂直Y轴指向实际目标点的直线为X轴，按照右手定则确定Z轴。

地心惯性坐标系（OXiYiZi）：以地心O为坐标原点，地心与第i次点火点连线为Yi轴，在当前弹道平面内过地心并且垂直Yi轴指向当前虚拟目标的直线为Xi轴，按照右手定则确定Zi轴；OX0Y0Z0的Y0轴为脉冲弹道的初始关机点与地心的连线。

参考弹道：借鉴文献［9－10］，人为给定一组符合实际情况的关机点参数，其射程大于、小于或等于打击目标所需的射程。通常为了充分利用多脉冲提高导弹射程的能力，选取射程小于打击目标所需射程的弹道作为参考弹道。不失一般性，本文选取由关机点到真实目标点之间的能量最省弹道为参考弹道，如图1（a）中虚线所示。其关机点的极半径、速度大小、弹道倾角和方位角记为（rr，vr，θr，ζr），同理多脉冲弹道的关机点参数记为（r0，v0，θ0，ζ0）。图1（a）中的实线部分为多脉冲弹道，1，2，…，n为脉冲点火点，。令二者在关机点处的极半径和速度等参数相同、弹道倾角与方位角等参数不同，即

式中：Δθ0和Δη0分别为多脉冲弹道与参考弹道在关机点处的弹道倾角差值和方位角差值。

多脉冲弹道初次关机时，其落地点为与真实目标有较大差距的虚拟目标；直到最后一次点火结束，导弹打击的目标才为真实目标。虚拟目标与真实目标之间的差距由Δθ0和Δη0决定。基于变射面的思想对Δθ0和Δη0进行优化，使虚拟目标与真实目标差距最大［5］，从而缩短敌方预警反应时间，提高导弹的突防能力。

图1（b）为子弹道示意图。如图1（b）中所示，相邻两次点火点（A、B分别为i次和第i＋1此点火点）之间的弹道为子弹道。导弹脉冲点火n次，则有n＋1段子弹道。导弹在i次点火后，以点火点A作为关机点，在坐标系OXiYiZi中按照开普勒轨道定律飞行。飞行到B点时，进行第i＋1次点火，此时点火点的极半径为ri＋1，该段弹道的射程角为Δfi＋1，飞行时间为Ti＋1，点火前后弹道面的夹角为Δηi＋1（即点火前后方位角差值）。从坐标系OXiYiZi到坐标系OXi＋1Yi＋1Zi＋1的转换矩阵［20］为

同理，可求得参考坐标系OXYZ到坐标系OX0Y0Z0的转换矩阵L0（Δ f0，Δη0），Δf0＝0°。

1．2 第i＋1次脉冲点火

本文设计的多脉冲弹道是由位于n＋1个共原点坐标系里的子弹道组成。在每个坐标系中将点火后的弹道参数作为关机点参数计算下次点火前的弹道参数。图2为导弹第i次点火后在坐标系OXiYiZi中的子弹道，其在XiOYi面内飞行，没有Zi方向上的速度与位移。直线CD表示点火点当地的水平线。令ri、vi和θi分别表示在该子弹道上关机点的极半径、速度大小和弹道倾角，（x，y，z）为导弹的空间位置，vx、vy和vz为沿各方向的速度分量，各变量的上标“－”和“＋”分别表示点火前和点火后，下标i表示在坐标系OXiYiZi中（下文同），则导弹i次点火后的弹道参数为

根据式（3）及文献［21］可得第i段弹道的轨道参数为

式中：μ 为地球引力系数；υk，i、vi、ei、pi、θi、ai、bi和ci分别为该轨道的能量参数、导弹速度大小、离心率、半通径、弹道倾角、长半轴、短半轴和焦距。

计算i次点火时的偏近点角Ei0及对应的真近点角

第i次点火完成并飞行Ti＋1时间后，导弹偏近点角为真近点角为则有

第i＋1次点火前的轨道参数［21］为

导弹的位置与速度大小分别为

式中：x－i＋1、y－i＋1、z－i＋1、v－x，i＋1、v－y，i＋1和v－z，i＋1为导弹第i＋1次点火前在坐标系OXiYiZi中的弹道参数。

第i＋1次点火时，脉冲速度增量为ΔVi＋1（大小为ΔVi＋1），方向角为σi＋1和γi＋1，则有

由式（10）可得

坐标系OXiYiZi到坐标系OXi＋1Yi＋1Zi＋1的转换矩阵为Li＋1（Δfi＋1，Δηi＋1），点火后导弹在坐标系OXi＋1Yi＋1Zi＋1中的位置与速度参数组成向量Si＋1。坐标系OXi＋1Yi＋1Zi＋1中的Yi＋1轴为点火点与地心的连线，Yi＋1轴垂直当地水平面即Xi＋1轴与当地水平面平行，所以点火后的弹道倾角为

在坐标系 OXi＋1Yi＋1Zi＋1中将Si＋1和θi＋1作为关机点参数计算第i＋1次点火前的弹道参数。

参考坐标系OXYZ 到坐标系OXi＋1Yi＋1Zi＋1的转换矩阵Ci＋1为

经过n次点火，导弹在坐标系OXYZ中的落地点坐标为（xtf，ytf，ztf）。

2 多脉冲机动弹道突防策略分析

2．1 突防策略分析

图3为节点航迹搜索示意图，图中从关机点到目标点之间有3条弹道，其中弹道1和弹道2为多脉冲弹道，弹道3为参考弹道。图3中有个威胁源；oj（j＝1，2，…，） 为威胁源的中心；Dj为每个威胁源的拦截范围；tmi（m＝1，2）为第m条弹道的第i次脉冲点火时刻；tmi＋τ为第m 条弹道在第i次点火后敌方探测系统能够准确确定弹道的最早时刻；dij（j＝1，2，…，） 为第i段子弹道与第j个威胁源中心的最短距离。此外，定义ti为任意弹道的第i次点火时刻。

弹道1为传统的无人机避障航迹。导弹没有穿过威胁源，而是从威胁源的边缘绕飞过去。最后从突防概率最高的方向进入威胁源，击中目标，称为机动方式1。

弹道2不同于传统无人机避障航迹规划，规划中考虑了导弹防御系统延迟τ这个因素。在满足一定条件的情况下，导弹可以穿过威胁源而不被拦截，称为机动方式2。具体情况如下：

1）ti＋1－ti≤τ

当子弹道的飞行时长小于防御系统延迟时，导弹无法被敌方防御系统确定并被拦截，因此是安全的。

2）ti＋1－ti＞τ

当子弹道的飞行时长大于防御系统延迟时，导弹在ti时刻点火，从ti＋τ到ti＋1之间的弹道到各个威胁源的最短距离dij大于对应威胁源的拦截范围Dj，那么这段子弹道是安全的。

当子弹道的飞行时长大于防御系统的延迟时，敌方防御系统有足够的时间来确定并拦截导弹。假如导弹在ti时刻机动，弹道发生了改变，由于系统延迟，敌方探测系统能够完全确定弹道的最早时刻是ti＋τ。假如ti＋τ时刻导弹在威胁源之外，那么导弹此时无法被拦截。假如从ti＋τ到ti＋1之间弹道处于所有威胁源之外，那么认为这段弹道是安全的。对于其他子弹道，可依此类推。以图3中的弹道2为例，t21＋τ与t22之间的弹道到威胁源j的最短距离为d11，威胁源1的拦截范围为D1（d11＞D1）。该段弹道与威胁源之间关系依次为：d12＞D2，…，d1j＞Dj，所以该段弹道是安全的。

通过以上两种机动方式，即可实现导弹中段的智能规避突防。

2．2 弹道设计问题转化

图4 中，（x0，y0，z0）和 （xt，yt，zt）分 别 为 给定的起点与终点位置。图4（a）表示无人机避障航迹规划中一条航迹链表，每个节点记录了航迹节点的空间坐标 （ux，i，uy，i，uz，i）（i＝0，1，…，n）及对应的状态变量Bi；（ux，t，uy，t，uz，t，Bt）为最终状态信息。Bi含有当前节点的以下信息：①节点满足航迹约束条件的情况；②该节点与下一个节点之间的航迹段是否可行；当且仅当航迹链表中所有节点与航迹段都可行时，航迹才可行。所以航迹集合中存在可行航迹及不可行航迹。在此基础上，利用评价函数对每一条航迹的进行评价，搜索得到最优航迹。

图4 （b）所展示的为多脉冲弹道Pj（j＝1，2，…）。将点火点作为规划的节点，第1个节点为初始关机点，最后1个节点为真实的目标点。节点个数固定，节点与节点之间的航迹不再是直线段，而是满足开普勒轨道方程的椭圆弹道。图4（b）用点火间隔Ti代替图4（a）中节点在空间中的位置。因为在已知Ti的情况下，通过开普勒方程可得到Ti时间后导弹的位置，即当前节点的空间坐标。在多脉冲弹道设计中，弹道链表的节点参数为 （Ti，σi，γi，Ni），当前节点的弹道参数Si、θi及Ti＋1共同决定了下个节点的空间位置。Ni为状态变量（N0和Nt分别为初态和终态），记录以下信息：①脉冲点满足弹道约束条件的情况；②当前点火点到下次点火点之间的子弹道是否可行；③该段子弹道与威胁源的关系。当Pj中所有节点及子弹道都可行时，弹道Pj才是可行的。

通过上述转换，可将多脉冲中段规避突防弹道的设计问题转化为无人机避障航迹的规划问题。在以有分析基础上，基于评价函数对弹道进行评价，再利用搜索算法可找到适应值最高的弹道。

2．3 子弹道与威胁源距离计算

计算子弹道与威胁源的距离采用以下步骤：

步骤1 将坐标系OXYZ中的威胁源Dj转换到子弹道所在坐标系OXiYiZi中，并投影到当前弹道平面内，得到投影g。

步骤2 视第i段子弹道为标准椭圆的一段，将其与g转换到标准椭圆所在的坐标系中。

步骤3 在标准椭圆坐标系中，利用椭圆参数方程计算g与子弹道的最短距离，得到威胁源j与第i段子弹道的距离。

通过上述方法，将三维空间中点与弹道的距离问题转换成二维平面内点到椭圆的距离问题。

如图5所示，过地心O以第i段椭圆弹道的近地点指向远地点的直线为Yc轴，在弹道平面内以过地心且垂直Yc轴的直线为Xc轴，建立直角坐标系XcΩOYc。以第i段椭圆弹道所在的标准椭圆的中心i（i＝1，2，…，n＋1）为Ω原点建立焦点在Y0轴上的直角坐标系X0iY0并建立辅助圆。

根据式（7）的定义可知，ti＋1、ti＋τ时刻导弹的偏近点角分别为和，根据式（2）和式（8）可得到从XcOYc到XiOYi的转换矩阵l （）为

在Ω标准椭圆参Ω数方程中，定义：ti＋τ时刻，导弹和Ωi的连线与ΩiX0的夹角为αi；ti＋1时刻，导弹与i的连线与iX0的夹角为βi。则有

根据式（4）给出Ω的椭圆参数，可知两时刻之间的弹道在平面X0iY0中用参数方程表示为

1）ti＋1－ti≤τ

第i段子弹道与第j个威胁源的距离为

式中：k为威胁源的距离常数。

为了使优化算法更快地收敛，根据威胁源拦截范围的不同对k作如下定义：

2）ti＋Ω1－ti＞τ

假设j在坐标系OXYZ 中的坐标为），在坐标系 OXiYiZi中的坐标为），在 当Ω 前 弹 道 平 面 内 的 投 影 为，则在 X0iY0面中的投影为

此时，子弹道到威胁源的距离为

3 弹道的搜索与评价

3．1 威胁源性能参数

本文选取SM－3作为威胁源分析。SM－3导弹包括Block 0、Block I和Block II系列。查阅文献［17］可知现役SM－3的最大射程为600km，最大拦截高度为160km。未来部署的Block II2A的射程可达1 200km，拦截高度为500km。多个SM－3拦截阵地可以相互通信，联合在一起。通过这种方式组成的“威胁网”的威胁程度大于导弹各自威胁程度之和。

3．2 弹道约束表达与分析

下文在讨论约束时，若无单独说明，均视为在当前子弹道所在的坐标系OXiYiZi中。

1）最小及最大航迹段长度

通过点火间隔Ti来控制子弹道的长短。

a）最小子弹道长度：导弹点火前需要一定的时间来调整弹体姿态及发动机喷嘴方向，假设其所需的调整时间为Tmin，则可将约束表示为

最后一次点火结束后，导弹按照传统弹道落地。如果打击目标在威胁源内，Tn＋1必须小于τ时才能突防成功，则有

b）最大子弹道长度：最大子弹道长度为导弹不点火，从关机点到落地点的飞行时间，设其为Tmax，约束表示为

2）最大拐弯角及最大爬升／下滑角

a）在弹道设计中，通过控制脉冲作用的角度来限制导弹最大（最小）的拐弯角及爬升角。为了使脉冲点火增加导弹的射程，要求点火时脉冲与导弹速度的夹角为锐角，即

b）为了迷惑敌方，由初始关机点决定的虚拟目标与实际目标的距离越远越好。在击中目标、满足距离与时间要求的前提下，多脉冲弹道与参考弹道在关机点的弹道倾角与方位角差值应满足：

3）最低飞行高度约束限制

本文中的最小高度约束为地球半径R，根据式（3）可得

4）端点约束

弹道设计中的端点约束为初始与终端约束。初始约束与参考弹道的关机点参数一致，

为了能击中目标，导弹需要满足的终端约束为

为了保证导弹的攻击效果，终端弹道参数还需要满足速度和落角约束，即

式中：vtf和θtf分别为导弹的落点速度与弹道倾角；vf为落点速度；θf为落地点弹道倾角；下标min和max分别表示相应物理量的最小值与最大值。

5）威胁指数

第i段子弹道受到第j个威胁源的威胁指数FTAJ由Ti和dij决定，即

3．3 性能指标的选取

本文设计多脉冲弹道是为了提高弹道导弹的突防能力。因此，除了考虑飞行时间最优外，还需考虑多脉冲弹道对敌方探测及防御系统的影响。

“虚拟落点”表示敌方探测系统依据点火前的弹道数据预测的导弹落地点。图6为多脉冲对弹道落点的影响示意图。如图所示，1，2，…，n为脉冲点火点，n＋1为最终落地点；2′，…，i′，n′为“虚拟落点”；R1，R2，…，Rn为相邻“虚拟落点”之间的距离。Ri的存在使得敌方在导弹点火后需要重新确定其落地点位置，其值越大对敌方的误导性也越大即导弹突防能力更高；所以在优化过程中，也将Ri作为优化指标之一。

考虑到以上因素，本文采用如下优化函数：

式中：Tt为总的飞行时间；w1，w2，m1，…，mn为权值，且都大于零；Rref为弹道落点差值的参考值，Tref为参考飞行时间，均用来对指标函数作无量纲处理。在实际弹道设计中，权值w1，w2，m1，…，mn依据敌方防御及探测系统的部署情况与能力的强弱来选取。

3．4 基于遗传算法的弹道设计

为了提高计算效率，采用实数编码的方式编写染色体｛Δθ，Δη，T1，…，Tn，γ1，…，γn，σ1，…，σn｝。

假设一共点火n次且有个威胁源，则每条染色体含有变量个数为3n＋2，每一条染色体Pj代表一条弹道。

优化中需要满足的不等式约束Ωi为

不考虑弹道终端的速度与角度约束，只考虑其位置约束。因此优化中需要满足的等式约束i：

基于以上分析，航迹评价函数为

式中：U为惩罚系数。

4 仿真实验算例

4．1 仿真参数

采用文献［15］中的仿真例子，假设敌方防御系统的延迟时间为4min，导弹需要4次点火，打击距离关机点4 666km外的目标。仿真中的参考弹道及拦截阵地的参数如表1和表2所示，表3仿真硬件环境参量。

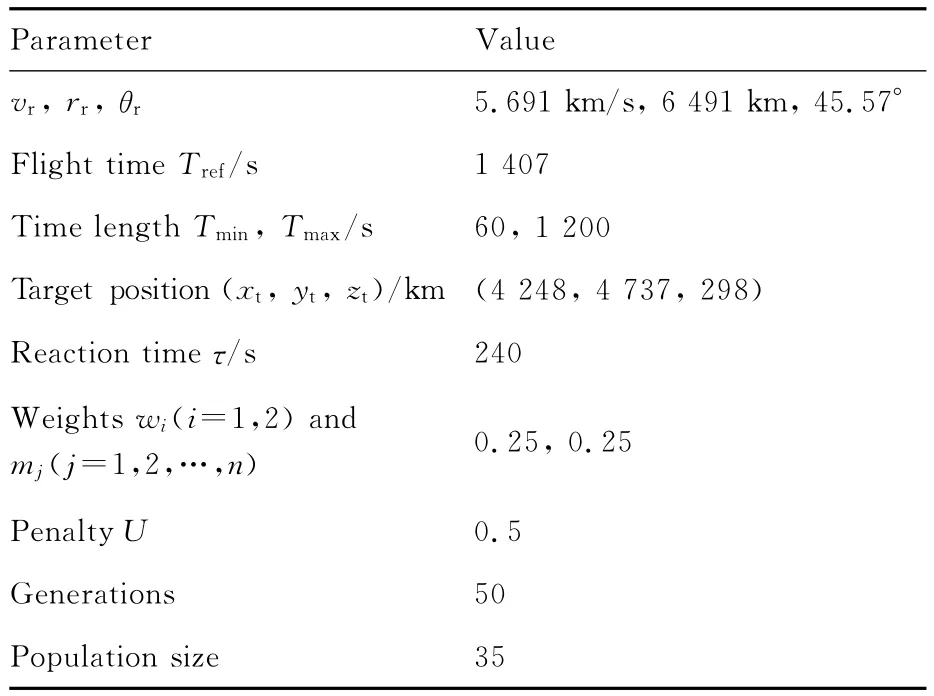
表1 仿真参数Table 1 Parameters of simulation

表2 威胁源参数Table 2 Parameters of threats

表3 硬件环境Table 3 Hardware environment

4．2 仿真分析

分析过程中，导弹点火时获取的速度增量大小ΔV 的取值范围为100～500m／s，每隔10m／s取一个值进行仿真分析。对于每个ΔV，成功优化30次后终止，取JGA值最小的一组弹道。选取ΔV＝250m／s、300m／s的例子对机动方式1进行仿真分析，优化结果见表4与表5。选取ΔV＝360m／s、410m／s例子对机动方式2进行仿真分析，其优化结果如表6与表7所示。表中：Tcost为优化所需的时间；ΔVx，ΔVy和ΔVz分别表示速度增量在3个方向上的分量；i表示第几次点火。

图7和图8分别为采用两种机动方式的多脉冲弹道与参考弹道在三维弹道、飞行高度h、飞行速度大小v 3个方面的对比（均在参考坐标系OXYZ中，下文同）。图7中，5条弹道从相同的关机点出发，经过若干时间的飞行，击中相同的目标。参考弹道不采取任何机动突防措施，将在威胁源1或3被敌方拦截。除参考弹道外，其余4条弹道都是由差异较大的5段异面子弹道组成。

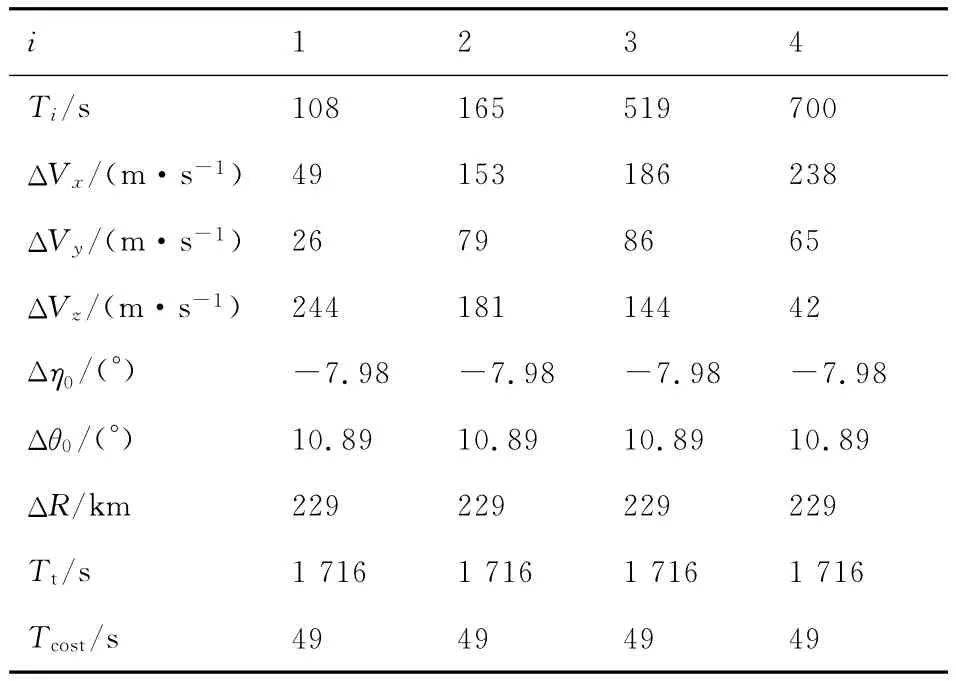
表4 机动方式1的仿真结果（V＝250m／s）Table 4 Simulation results of the first maneuver mode（V＝250m／s）

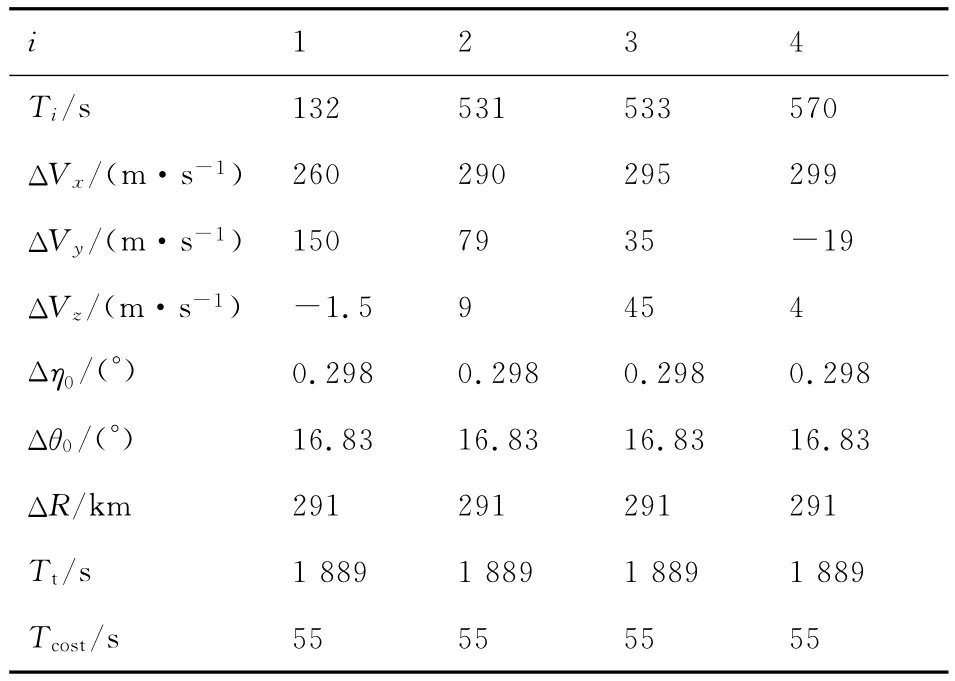
表5 机动方式1的仿真结果（V＝300m／s）Table 5 Simulation results of the first maneuver mode（V＝300m／s）

表6 机动方式2的仿真结果（V＝360m／s）Table 6 Simulation results of the second maneuver mode（V＝360m／s）

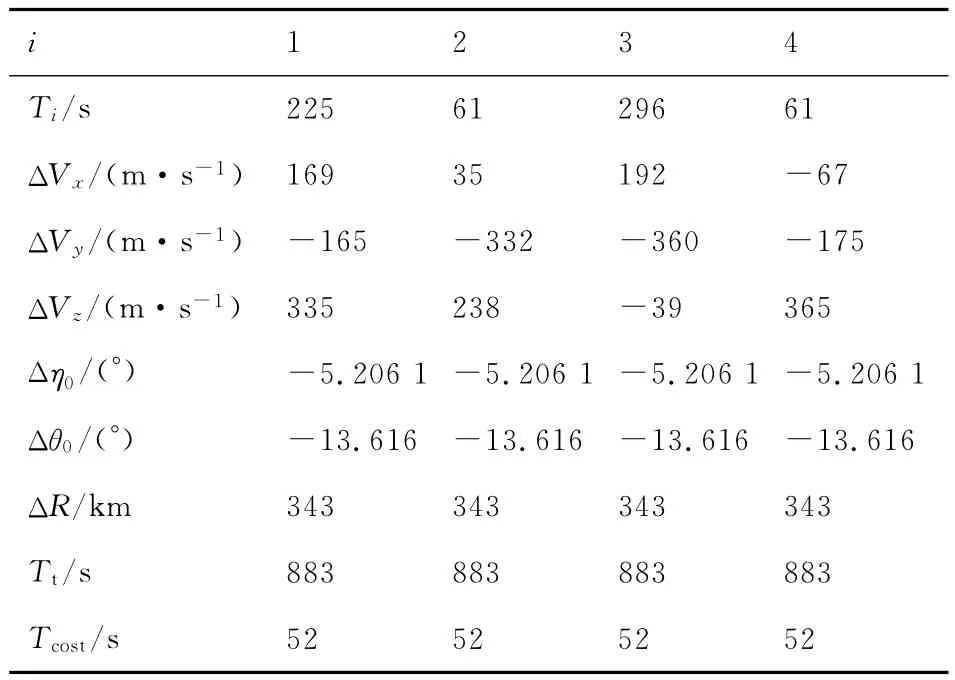
表7 机动方式2的仿真结果（V＝410m／s）Table 7 Simulation results of the second maneuver mode（V＝410m／s）

依据表4和表5中的数据，结合图7分析有如下结论：

1）ΔV＝250m／s、300m／s的弹道采用第1种机动方式，其与传统无人机避障航迹类似，飞越威胁源，最后击中目标，全程都处于威胁源外，敌方拦截系统无法进行拦截。

2）ΔV＝360m／s、410m／s的弹道采用第2种机动方式，弹道穿越威胁源。在敌方探测系统确定导弹弹道之前飞出威胁源，使敌方拦截系统无法拦截。

3）ΔR的范围为229～343km，说明敌方探测系统必须重新采集导弹点火后的数据并确定其新的落地点。所以，直到导弹最后一次点火结束，敌方才能确定其真实落点即敌方预警时间被大大缩短。

4）由表4和表5可知，设计及优化弹道所需的时间不超过60s。同时在蒙特卡罗打靶试验中，设计弹道所需时间也不超过60s。这说明本文提出的中段规避突防策略可以根据瞬息变化的战场情况，迅速地做出有针对性的反应，在很短时间内得到一条线下规划弹道，从而进一步提高导弹的突防能力。此外，导弹可以随时根据新的目标信息，在距发射前很短的时间内规划出最优弹道，提高了导弹打击任务的灵活性。

5）所有的多脉冲弹道最后都击中了目标，说明本文提出的中段突防策略能保证导弹的打击精度。

以上结论说明采用两种机动方式得到的突防弹道都可以使导弹成功规避敌方拦截系统，这也说明本文提出的中段规避突防策略是可行且有效的。

依据表4和表5中的数据，结合图8分析有如下结论：

1）在飞行高度、时间方面机动方式1大于参考弹道，参考弹道大于机动方式2。根据二体轨道理论，导弹要维持椭圆弹道，导弹的平均速度增加，会导致其飞行高度的降低，导弹的平均速度降低，其飞行高度会增加。

2）相比参考弹道：机动方式1的平均飞行速度降低，飞行时间延长了21．25%～36．67%；机动方式2平均飞行速度提高，飞行时间缩短了30．14%～37．24%。通过多脉冲机动可以调节导弹的飞行速度、时间、弹道高度，根据突防需求设计满足要求的弹道。

以上仿真分析结果说明，本文提出的中段规避突防策略可以有效地改变弹道参数，使敌方探测系统的探测数据失真，误导及迷惑敌方的探测系统，提高导弹的突防能力。

4．3 防御系统延迟对弹道规划的影响

为了研究系统延迟τ对弹道规划的影响，在其他参数不变的情况下，改变其大小，观察多脉冲突防弹道的变化情况。

仿真中，τ＝120～300s，间隔时间为5s，ΔV＝250m／s，其他仿真条件与4．1节一致。以τ＝180s和τ＝230s的情况进行举例分析，图9为突防弹道、导弹飞行高度及速度随防御系统延迟的变化而变化得关系，图10为穿越弹道的总飞行时间随系统延迟的变化关系。1）采用本文提出突防策略可以得到两种弹道：一种是从威胁源拦截范围上限飞过，为飞越弹道；另一种是从威胁源中穿过或从其拦截下限飞过，表现形式为穿越威胁源，为穿越弹道。

2）τ＝180s时，只有飞越威胁源的弹道，无穿越弹道。τ＝230s时，飞越及穿越威胁源的弹道同时存在，且都满足导弹的突防要求。但是两种弹道的飞行高度及飞行速度差别很大。

3）根据图9可知，飞越弹道的飞行高度高，飞行速度慢，飞行时间长；穿越弹道的飞行高度低，飞行速度快，飞行时间短。

4）当τ≥210s时，飞越及穿越弹道会同时存在，当τ＜210s时，只有飞越弹道。具体变化关系如图10所示，随着系统延迟的增加，导弹的飞行时间被缩短。所以，可以根据时间、距离及打击任务的要求增加约束，对弹道进行取舍。

5 结 论

1）多脉冲弹道设计问题可以转变成无人机避障航迹规划问题，并使问题得以简化。从而可以利用已经比较成熟的无人机避障航迹规划方法来解决多脉冲弹道设计问题。这样能在保证导弹打击精度前体下实现导弹的成功突防。

2）综合考虑敌方探测及防御系统，使导弹获得反预警及反拦截能力，确实能提高其突防能力。将敌方拦截系统视为障碍物，并处理成迹规划中的多约束是可行的。根据实时获取的敌方防御系统信息及时地改变规划中的约束条件，得到最优的线下规划弹道，从而提高导弹打击任务的灵活性。

3）本文提出的突防策略即可以获得平均飞行速度大、飞行时间短且弹道高度低的弹道，也可以获得平均飞行速度小、飞行时间长且弹道飞行高度高的弹道。根据具体突防需求选择最合适的机动方式。

4）防御系统延迟会影响多脉冲弹道的规划，要根据实际需要合理规划弹道，使弹道的突防能力最大。

5）在其他条件固定时，如何选取点火次数、点火次数增减的规则、点火次数对弹道规划的影响需要进一步进行深入的研究，也将是下一步研究的重点。

［1］ 鲜勇，李少朋，雷刚，等．弹道导弹中段机动突防技术研究综述［J］．飞航导弹，2015，18（9）：43－46．XIAN Y，LI S P，LEI G，et al．Discussion of ballistic missile penetrating missile defense system［J］．Aerodynamic Missile Journal，2015，18（9）：43－46（in Chinese）．

［2］ 周啟航，张刘，霍明英，等．弹道导弹中段突防弹道设计与验证［J］．光学精密工程，2015，36（9）：2645－2655．ZHOU Q H，ZHANG L，HUO M Y．et al．Ballistic missile midcourse penetration trajectory design and validation［J］．Optics and Precision Engineering，2015，36（9）：2645－2655（in Chinese）．

［3］ 鲜勇，李少朋，李振华，等．基于梯度粒子群算法的纵横向机动跳跃弹道设计及优化［J］．弹道学报，2015，27（3）：1－6．XIAN Y，LI S P，LI Z H，et al．Design and optimization of vertical wavy and crosswise maneuvering trajectory based on grads particle swarm algorithm［J］．Journal of Ballistics，2015，27（3）：1－6（in Chinese）．

［4］ 李广华，张洪波，汤国建．高超声速滑翔飞行器典型弹道特性分析［J］．宇航学报，2015，46（4）：397－403．LI G H，ZHANG H B，TANG G J．Typical trajectory characteristics of hypersonic glide vehicle［J］．Journal of Astronautics，2015，46（4）：397－403（in Chinese）．

［5］ 鲜勇，刘炳琪，王安民，等．变射面弹道横向转弯飞行程序的设计与优化［J］．弹道学报，2014，26（4）：30－35．XIAN Y，LIU B Q，WANG A M，et al．Design and optimization of lateral turning flight programon changeable launching plane trajectory［J］．Journal of Ballistics，2014，26（4）：30－35（in Chinese）．

［6］ 明超，孙瑞胜，白宏阳，等．基于hp自适应伪谱法的多脉冲导弹弹道优化设计［J］．固体火箭技术，2015，38（2）：151－155．MING C，SUN R S，BAI H Y，et al．Optimizing design of trajectory for multiple－pulse missiles based on hp－adaptive pseudo－spectral method［J］．Journal of Solid Rocket Technology，2015，38（2）：151－155（in Chinese）．

［7］ 邓逸凡，李超兵，王志刚．一种基于轨道要素形式终端约束的航天器空间变轨迭代制导算法［J］．航空学报，2015，36（6）：1975－1982．DENG Y F，LI C B，WANG Z G．An iterative guidance algorithm using orbit element as terminal constraints for spacecraft orbit transfer［J］．Acta Aeronautica et Astronautica Sinica，2015，36（6）：1975－1982（in Chinese）．

［8］ 冯令兵，葛致磊，李宪强，等．弹道导弹被动段最优脉冲变轨方法［J］．指挥控制与仿真，2014，36（2）：114－117．FENG L B，GE Z L，LI X Q，et al．A study on the ballistic missile’s optimal impulse orbit transfer in the passive ballistic curve［J］．Command Control Simulation，2014，36（2）：114－117（in Chinese）．

［9］ GILLIS M P I．Optimal mid－course modication of ballistic missile trajectories：Air Force Institute of Technology Re－port［R］．Washington，D．C．：Wright－Patterson Air Force Base，1975．

［10］ DRUCKMANN E，BENASHER J Z．Optimal in－flight trajectory modifications for ballistic missiles and free rockets［J］．Journal of Guidance，Control，and Dynamics，2012，35（2）：462－470．

［11］ GUO Y，YAO Y，WANG S，et al．Maneuver control strategies to maximize prediction errors in ballistic middle phase［J］．Journal of Guidance，Control，and Dynamics，2013，36（4）：1225－1234．

［12］ GUO Y，YAO Y，WANG S，et al．Maneuver strategy of evader considering detection system［C］／Proceedings of AIAA Guidance，Navigation，and Control Conference．Reston：AIAA，2011．

［13］ 张广明，高普云，唐乾刚．导弹在被动段突防的脉冲式异面变轨方法［J］．宇航学报，2008，29（1）：89－94．ZHANG G M，GAO P Y，TANG Q G．The method of the impulse trajectory transfer in a different plane for the ballistic missile penetrating missile defense system in the passive ballistic curve［J］．Journal of Astronautics，2008，29（1）：89－94（in Chinese）．

［14］ 高普云，张广明，唐乾刚，等．导弹在被动段突防的脉冲式轴 向 加 速 方 法 ［J］． 宇 航 学 报，2008，29（4）：1126－1130．GAO P Y，ZHANG G M，TANG Q G，et al．The method of increasing velocity along its original velocity direction by the impulse firing for the ballistic missile to penetrate the anti－missile system in the passive ballistic curve［J］．Journal of Astronautics，2008，29（4）：1126－1130（in Chinese）．

［15］ 高普云，张广明，冯志刚，等．基于脉冲点火弹头空间机动的被动段弹道设计方法和数值仿真［J］．宇航学报，2009，30（3）：884－889．GAO P Y，ZHANG G M，FENG Z G，et al．The method of the trajectory design and numerical stimulation of the missile maneuvers in space based on the impulse firing in the passive curve［J］．Journal of Astronautics，2009，30（3）：884－889（in Chinese）．

［16］ 张斌，任军学，王一白，等．导弹在被动段轴向加速变轨弹道设计与优化［J］．北京航空航天大学学报，2010，21（6）：650－653．ZHANG B，REN J X，WANG Y B．Design and optimization on trajectory of increasing velocity along its original velocity direction by impulse firing for ballistic missile to penetrate anti－missile system in passive ballistic curve［J］．Journal of Beijing University of Aeronautics and Astronautics，2010，21（6）：650－653（in Chinese）．

［17］ 赵秀娜．机动弹头的智能规避策略研究［D］．长沙：国防科学技术大学，2006：10－25．ZHAO X N．The intelligent evasive strategy of the ma－neuver missiles［D］．Changsha：National University of Defense Technology，2006：10－25（in Chinese）．

［18］ 丁明跃，郑昌文，周成平，等．无人飞行器航迹规划［M］．北京：电子工业出版社，2009：49－50．DING M Y，ZHENG C W，ZHOU C P，et al．Flight path planning for unmanned aerial vehicles［M］．Beijing：Electronics Industry Press，2009：49－50（in Chinese）．

［19］ 张广明，高普云，唐乾刚，等．弹道导弹在被动段突防的平面脉冲式变轨方法［J］．弹道学报，2008，34（3）：83－86．ZHANG G M，GAO P Y，TANG Q G，et al．The method of the impulse trajectory transfer in a plane for the ballistic missile breaking through a defense line in the passive ballistic curve［J］．Journal of Ballistics，2008，34（3）：83－86（in Chinese）．

［20］ 贾沛然，陈克俊，何力．远程火箭弹道学［M］．长沙：国防科技大学出版社，1993：173－199．JIA P R，CHEN K J，HE L．Long－range rocket ballistics［M］．Changsha：National University of Defense Technology Press，1993：173－199（in Chinese）．

［21］ 刘暾，赵钧．空间飞行器动力学［M］．哈尔滨：哈尔滨工业大学出版社，2003：62－68．LIU D，ZHAO J．Aero spacecraft dynamics［M］．Harbin：Harbin Institute of Technology Press，2003：62－68 （in Chinese）．

［22］ 赵钧．航天器轨道动力学［M］．哈尔滨：哈尔滨工业大学出版社，2011：42－87．ZHAO J．Orbital dynamics ofspacecraft［M］．Harbin：Harbin Institute of Technology Press，2011：42－87 （in Chinese）．

Anti－warning－based anti－interception avoiding penetration strategy in midcourse

ZHOU Qihang1，LIU Yanfang1，＊ ，QI Naiming1，YAN Junfeng1，2
1．School of Astronautics，Harbin Institute of Technology，Harbin 150006，China
2．61906Forces，Langfang 065000，China

An anti－warning－based anti－interception avoiding penetration strategy is proposed for fully exploiting potential of the multi－pulse maneuvering and improving the midcourse penetration ability of ballistic missiles．With the interception system being regarded as threats and transformed into the constraint conditions，the multi－pulse trajectory design is turned into an obstacle avoidance path planning for the unmanned aerial vehicle，wherein the pulse ignition point and interval are regarded as the search nodes and step，respectively．The optimal ignition parameters are selected based on a comprehensive consideration of the detection system delay and the performance and deployment of the interception system．Influence of pulse increment and system delay on multi－pulse trajectory is studied Simulation results show that the proposed strategy can damage the convergence of enemy’s prediction algorithm by multi－pulse maneuvering，and the accuracy of hostile warning results is thus reduced．When the enemy’s prediction error sufficiently converges and the hostile warning is accurate enough，the missile is already being out of the range of interception．According to the latest information in battlefield，an optimal multi－pulse trajectory can be designed offline in 60s，which can increase（decrease）the flight altitude and the average flight speed，and shorten（prolong）the flight time by 20%－35%．

ballistic missile；multi－pulse；threat；obstacle avoidance；ballistic design；maneuvering penetration

2015－12－03；Revised：2016－01－26；Accepted：2016－04－07；Published online：2016－04－13 15：35

URL：www．cnki．net／kcms／detail／11．1929．V．20160413．1535．004．html

Shanghai Aerospace Science and Technology Innovation Fund（SAST201312）

V448．131

A

1000－6893（2017）01－319922－13

http：／hkxb．buaa．edu．cn hkxb＠buaa．edu．cn

10．7527／S1000－6893．2016．0116

2015－12－03；退修日期：2016－01－26；录用日期：2016－04－07；网络出版时间：2016－04－13 15：35

www．cnki．net／kcms／detail／11．1929．V．20160413．1535．004．html

上海航天科技创新基金 （SAST201312）

＊通讯作者 ．E－mail：lyf04025121＠126．com

周啟航，刘延芳，齐乃明，等．基于反预警的反拦截中段规避突防策略［J］．航空学报，2017，38（1）：319922．ZHOU Q H，LIU Y F，QI N M，et al．Anti－warning－based anti－interception avoiding penetration strategy in midcourse［J］．Acta Aeronautica et Astronautica Sinica，2017，38（1）：319922．

（责任编辑：张玉）

＊Corresponding author．E－mail：lyf04025121＠126．com