用位移法中“典型方程、转角位移方程”的观点进行弯矩分配的解释

陈百鸣

(富裕县水务局，黑龙江 富裕 161200)

用位移法中“典型方程、转角位移方程”的观点进行弯矩分配的解释

陈百鸣

(富裕县水务局，黑龙江 富裕 161200)

针对结构力学位移法中典型方程与转角位移方程的应用,根据长期的实践经验和体会,分析概括了位移法解决超静定结构的基本途径、典型方程的物理意义，以及弯矩分配计算等基本概念,最后给出了在位移法典型方程解释弯矩分配法中的弯矩分配过程和位移法“转角位移方程”弯矩分配中力矩传递过程的解释。

位移法；转角位移方程；超静定结构；弯矩分配

1 位移法的基本途径

对于力法解决超静定结构需要联立多元一次方程组，计算之复杂性是显而易见的，特别是用力法计算较复杂的刚架时尤为繁琐，往往要联立六元以上方程组。这样就迫使我们寻求新的途径解决计算这一新课题，在认识解决一项新课题之前，总是设法寻求一个解决问题的新途径，在这里，联想力法的思想方法就是遵循从已知到未知的过程，就是把新课题经过一系列的假定转化为老问题，进而解决。在力法处理超静定结构时，是将复杂的超静定结构去掉多余联系后变为静定结构来处理，那么对于较复杂的刚架来讲，究竟采取什么样的途径是仍需要解决的问题，我们知道超静定刚架是由若干个两端可转动的固定端单跨超静定梁[1](这与实际工程中单跨超静定是不符的，为了寻求解决问题的途径做这样的假定)所组成的，采取各个击破的办法分别计算每个单独杆件的端内力，再组合起来便为刚架整体结构的内力值。那么这个单独杆件的端内力又如何计算呢？对于超静定结构的内力不仅与外荷载有关，而且还与其形变有关，整体结构的形变引起整体结构的内力，经过分析得出关系式(1)、式(2)，即单独杆件的端内力与其形变存在下列关系：

(1)

(2)

此关系式在结构力学中称为转角位移方程，该方程给定了杆端力矩与杆端位移的函数关系，通过转角位移方程计算超静定结构各杆件的内力，进而求解超静定结构内力值，此方程是用位移法计算超静定结构的纽带。方程右边第一项固端力矩是假想单跨超静定梁在外力作用下产生的约束力矩，该值可用力法求解。为了计算上的简便，在结构力学中已列表给定了各种单跨超静定梁的内力值，方程右边第二项是杆端发生位移所需要的力矩，经过这样的转化，问题的关系归结为如何求出各单跨超静定梁的杆端位移，一旦求出各杆端的位移就不难求得其杆端内力，如何求得各杆端的位移，对于这个问题仍要联想到力法如何求得多余未知力，在力法求解未知力的途径是将基本体系恢复到原结构状态，恢复条件是结构形变的连续条件，即各多余联系处的形变为零。通过这个条件建立力法典型方程，通过方程组求解多余未知力，同样试图用力法典型方程的途径来解决问题的思想方法，通过建立位移法典型方程来求解未知位移，经过分析，超静定刚架的各弹性结点虽然在外力作用下发生了绝对变位，但不存在相对位移，用力矩观点解释即刚架各弹性结点的力矩代数和等于零，以这个平衡条件来建立方程即可计算出未知位移，这个方程即为位移法典型方程，即：

Qr+RP=0

(3)

式中：Qr是某弹性结点的各相邻杆端发生Q角位移所施加的力矩；RP是外力作用下某结点处由于加刚臂所产生的约束力矩。建立方程的条件是将基本体系恢复到原结构状态，典型方程(3)从物理意义上讲：是某一弹性结点在刚臂约束下、在外力作用下产生的抵抗力矩，经过原结构状态的恢复完全消耗在该弹性结点相邻各杆端发生绝对位移的过程中，即此抵抗力矩等于使该弹性结点相邻杆件产生绝对位移的力矩，对于多个弹性结点可联立方程组，对每个可位移的弹性结点分别列典型方程，组成方程组，解此典型方程求得未知位移，根据求得的位移值，利用转角位移方程计算出杆端弯矩，再进行组合。这就是位移法的基本思想方法，也是用位移法求解超静定结构的基本途径。

2 转角位移方程、典型方程的物理意义

2.1 转角位移方程

转角位移方程表达为：

(4)

(5)

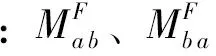
对于转角位移方程的直接解释：好比当外力施加在人体上，试图将人搬倒，当人体抵抗外力不想倾倒，则此人体所承受的外力矩最大，假如此人不抵抗外力或者少抵抗外力，顺势沿外力方向倒去或发生一定位移(折角)，此时人体所承受的外力矩就相应减小或等于零(人体完全倒下，则人体承受力矩为零)，转角位移方程完全揭示了超静定结构的内力与变形的函数关系。

2.2 位移典型方程

方程式(3)即为位移法中典型方程的基本型式，当杆端假想固定时杆端的抵抗力矩，从力法典型方程看是通过典型方程的建立，使基本体系完全恢复到原结构状态的过程，建立方程的条件是连续条件(即超静定结构的变形连续条件)即各多余联系处变位等于零。关于此位移法的典型方程的建立，同样由基本体系恢复原结构实际状态的过程，恢复条件是每个弹性结点的力矩代数和等于零，根据这个条件对每个弹性结点列典型方程，故典型方程的物理意义是超静定结构的每个弹性结点不存在相对位移，正是由于这个条件，用力矩观点解释即每个弹性结点力矩代数和等于零。

3 从弯矩分配法的思想方法看位移法两方程在弯矩分配上的解释

3.1 弯矩分配法的思想方法

对于力法与位移法求解超静定结构内力时，均采取联立方程组法求解超静定结构内力，尽管位移法的未知位移比起力法的未知力数目少，但对于复杂的超静定结构来讲，仍然克服不了两种方法的弱点——多元方程组。这样不仅需花费大量的工作，而且求解时不可避免的发生这样或那样的错误，这样就迫使我们寻求更为简捷的办法，根据转角位移方程的物理意义，当外荷载作用于超静定结构上时，由于外力作用，结构的各弹性结点产生一定的力矩，而这个力矩将使该弹性结点相邻的各杆件发生一定的位移(转角或线位移)，当以刚臂对弹性结点加以约束时，刚臂在外力作用下产生了抵抗位移的抵抗力矩，而当结构处于实际变形的状态下，则抵抗力矩完全消耗在弹性结点的位移过程中。在外力作用下，各杆件所获得的力矩值与杆件刚度有关，故弹性结点各相邻杆件所获得的力矩按刚度进行分配。根据这个原理过程，采取了逐步地、循序渐近地将基本体系恢复为原结构状态，求解各杆件的杆端力矩，该思想方法即是弯矩分配法的中心。它所遵循的原则是分配力矩、传递力矩、再分配再传递，直至收敛完毕。从力平衡的观点解释是不平衡达到平衡，再不平衡直至收敛平衡为止。它的基本要素是将外力引起的固端力矩进行分配，分配的弯矩进行传递，最终进行叠加。

3.2 典型方程、转角位移方程在弯矩分配法过程中的解释

3.2.1 用位移法典型方程解释弯矩分配法中的弯矩分配过程

前面对位移法典型方程的物理意义已做了说明，超静定结构在外力作用下，各弹性结点仅发生绝对位移，不存在相对位移[3]，确切一点讲，超静定结构在外力作用下，各弹性结点仍保持原有的相对几何形状，不发生相对位移，这样就提供了一个条件——每个弹性结点在外力作用下所承受的力矩等于假想刚臂约束的约束力矩，即总力矩代数和等于零，当刚臂放松的时候刚臂的抵抗力矩完全消耗于各弹性结点的绝对变形过程中。

对于弯矩分配法中弯矩分配过程，即是将外力引起的弹性结点上的刚臂约束力矩按弹性结点相邻各杆的刚度进行一次分配(从广义上讲其他各弹性结点在外力作用下，发生了变形导致对该弹性结点的影响力矩同样按各杆刚度参加一次分配)分配力矩与刚臂抵抗力矩大小相等，符号相反。这样，刚臂的抵抗力矩与弹性结点发生实际转动所需力矩恰好相等，即它们的代数和等于零。这个过程也正体现出位移法中典型方程的物理意义。

3.2.2 从位移法“转角位移方程”看弯矩分配中力矩传递过程

关于转角位移方程的物理意义上面已做了说明，对某一单独杆件，即假想单跨超静定梁，它的杆端力矩不仅与外力作用下直接影响的力矩值有关。而且与其变形有关。对超静定整体结构而言，某一弹性结点的邻近各杆端弯矩除外力作用下产生的固端弯矩以外，尚与该弹性结点的位移有关，与其他结点在外力作用下发生位移所波及到该结点的变形有关。通俗一点讲，对于超静定结构当外力作用结构某一部位时，它的整个结构均承受一定的外荷载。从应力的角度讲，整个结构的每一个部份都产生应力值，这一点，转角位移方程已给定了应力与应变的函数关系式，方程的右边第一项是施加外力时某弹性结点加以刚臂约束时所承担的弯矩，右第二项是外力作用下某弹性结点本身发生形变所付出给的力矩值，第三项第四项则是由于外力作用其他结点发生形变后所波及某弹性结点的变形相当的力矩值，这个方程式明确地表达超静定结构在外力作用下，结构整体发生的内力情况。

在用弯矩分配法计算超静定结构时，它的第二个要素是力矩传递，当超静定结构有两个或以上的弹性结点时，则两个弹性结点在外力作用下所承担的力矩相互影响[4]，当分别将每个弹性结点放松恢复原结构状态时，对某一弹性结点来讲，将抵抗力矩分配给此结点邻近的各杆端，此外相邻弹性结点刚臂放松时，对于两弹性结点中间这一杆件来讲，后一结点邻近的杆端将分配获得一定力矩，此力矩又按该杆件的两端连接性质传递到前一结点相邻的杆端。至使前弹性结点将传递来的力矩再次分配给相邻的各杆端。反复几次直至收敛为零或接近为零为止。这个传递过程正体现出转角位移方程右边的第二项、第三项、第四项的存在，也就是说，根据转角位移方程的第二项、第三项、第四项才推导出弯矩分配法的传递过程。所不同的是位移法通过解析式来表达超静定结构的内力分布，而弯矩分配法较直观地表达出超静定结构的内力分布，弯矩分配法中的力矩传递过程正是应用位移法转角位移方程而推导的。

3.2.3 从位移转角方程看弯矩分配的最终叠加

在弯矩分配中，为了获得超静定结构的各杆件的杆端弯矩，必须将多次的分配力矩、多次传递力矩，以及在外力作用下假想刚臂的约束力矩进行叠加，根据转角位移方程的物理意义，弯矩分配法中叠加的几项即是该方程中右边的每一项，通过叠加更明显地体现出转角位移方程的物理意义。从弯矩分配法叠加过程中明显地看到转角位移方程的每一项确确实实地客观存在，而转角位移方程的每一项也确确实实地对应着弯矩分配法中的分配力矩、传递力矩，以及外力作用刚臂所承担的约束力矩。

4 结 论

在结构内力分析计算过程中，组成整体结构各杆件的内力除与外荷载有关外，各杆件的相对刚度又是决定其内力值的主要因素，静定结构与超静定结构的内力分析即区别于此。

对于超静定结构的内力分析计算的传统方法——力法、位移法、弯矩分配法，从解决问题的思路到基本概念、基本理论、基本计算方法，虽存在着看似本质方面的不同，但透过其计算方法的现象，尚看到其理论方面的内在联系。

从位移法中的两个方程物理意义上看：转角位移方程揭示了超静定结构内力与变形的函数关系；典型方程体现出超静定结构每个弹性结点不存在相对位移的几何可变现象。从位移法中的两个方程还可以体会到弯矩分配法的力矩分配、传递、再分配再传递，及叠加的渐近过程。

[1] 陈锦艳.有固定端的等截面单跨超静定梁的快速解法[J].中国科技信息，2008(18)：75-77.

[2] 李秀梅.位移法的基本概念及典型方程的建立[J].学周刊，2011(28)：11-12.

[3] 苏勒德.位移法在结构力学中的应用[J].河南科技，2012(18)：62-62.

[4] 俞瑞荣. 等截面单跨超静定梁固端弯矩的一种解法 [J]. 无锡职业技术学院学报，2006(2)：57，96.

陈百鸣(1975-)，男，黑龙江克山人，高级工程师，从事水利规划设计工作。E-mail：fycbm@126.com。

TU501；TB301

A

2096-0506(2017)10-0052-04