反应谱分析法在重力坝抗震性能分析中的应用研究

龚 勋，辛 欣，李 萌，邓 源，李悠然

(1.惠州市华禹水利水电工程勘测设计有限公司，广东 惠州 516000；2.三峡大学 水利与环境学院，湖北 宜昌 443002)

反应谱分析法在重力坝抗震性能分析中的应用研究

龚 勋1，辛 欣2，李 萌2，邓 源2，李悠然2

(1.惠州市华禹水利水电工程勘测设计有限公司，广东 惠州 516000；2.三峡大学 水利与环境学院，湖北 宜昌 443002)

本文首先对坝体进行静力分析，采用ANSYS中PLANE182单元模拟某重力坝坝体，探究坝体在自重及水压力作用下的应力与变形；然后运用反应谱分析法对坝体进行地震动力分析，包括采用模态分析法提取模态，确定大坝自振频率及振型，结合反应谱曲线方程得出反应谱谱值，然后进行反应谱分析及模态扩展，最后对模态进行合并。求得坝体在各阶模态下的应力及位移响应。结果表明:在地震设防烈度为8°的情况下，研究坝体的变形及强度均在可控范围内;最大应力、应变主要集中于大坝的中上部、坝踵、坝趾等处，在今后设计和施工中应引起足够的重视。

抗震性能；反应谱分析法；模态分析； PLANE182单元；地震设防烈度

反应谱法基于标准反应谱曲线，以惯性力的形式将地震时坝体基岩面的加速度置于其上，探究其动力响应情况。反应谱法是由Biot N A于1943年提出，并于1956年，由Newmark N M第一次将反应谱法应用于工程计算。我国的抗震规范中也引用了反应谱法。反应谱法的产生、应用，开创了将动力学方法用于地震分析的新思路。地震作用虽然复杂且不易发现规律，但经过多年的研究，可以用反应谱法获得近似解[1]。本文采用反应谱分析法，选择某120 m高坝非溢流面为典型断面，在正常蓄水位工况下，对其进行地震动力分析，探究其位移及应力响应规律，评价其抗震性能。

1 材料与方法

1.1 振型反应谱分析法

根据结构动力学的基本求解理论可得多自由度体系的弹性动力方程为:

[K]{δ}+[C]{δ′}+([Md]+

[Mp]){δ″}={F(t)}

(1)

式中：[K]为总体刚度矩阵；{δ}为位移矩阵；{δ′}为结构速度矩阵；{δ″}为结构加速度矩阵；{F(t)}为节点等效荷载矩阵；[C]为结构的总体阻尼矩阵；[Md]为结构总体集中质量矩阵；[Mp]为结构总体附加质量矩阵，由作用在结构上的动水压力求得。

对于无外荷载与阻尼的自由振动问题，阻尼项{δ′}=0，外力{F(t)}=0，于是动力方程变为：

[K]{δ}+([Md]+[Mp]){δ″}=0

(2)

结构做自由振动时，可将各质点视为做简谐运动，为了确定结构自由振动的固有频率及相应的振型,需要考虑简谐运动的解即为：

{δ}={δ0}sinωt

(3)

式中：ω为结构自由振动固有频率；t为时间；{δ0}为位移{δ}的振幅列向量，即振型。

将式(3)代入式(2)，得广义特征方程为：

([K]-ω2[M]){δ0}=0

(4)

式中：ω2为结构自由振动的特征值；[M]=[Md]+[Mp]。

方程组有非零解的条件为：

([K]-ω2[M])=0

(5)

1.2 计算模型及参数

某重力坝坝高120 m，坝底宽度76 m，坝顶宽度10 m，因为坝体结构较简单，垂直坝轴线方向的坝体断面基本相同，其受力分布也大致相同，选用典型非溢流面对大坝进行静力及地震动力分析。

选用PLANE182单元模拟重力坝坝体，通过设置单元选项“K3”为“Plane strain”来设定，本实例分析采取平面应变模型进行分析，大部分单元为4结点四边形单元，少数为4结点三角形单元。共划分464个结点、412个单元。有限元计算所得的应力是在整体坐标系下进行的。

大坝抗震性能分析的各计算参数如下：

(1)大坝采用的材料参数为：C30混凝土，弹性模量E=31.5 GPa，泊松比ν=0.2，容重γ=2.42 kN/m3。

(2)计算分析取大坝正常蓄水位75 m。

(3)水的质量密度1000 kg/m3。

(4)大坝地震烈度取8°，地震水平方向加速度值取0.2 g。网格划分见图1。

图1 坝体有限元模型

2 坝体静力分析

2.1 静力分析

本文选取大坝蓄水期正常蓄水工况进行分析，大坝上下游水深分别为75 m和17 m。主要荷载为:坝体自重、大坝正常蓄水位时上下游的水压力、坝底扬压力等，泥沙压力本文中不予计算。

坝体变形结果见图2。X方向(顺水流方向)与Y方向(竖直方向)的变形位移见图3。

图2 坝体整体变形图

坝体X方向位移最大值发生在坝顶处，为12.12 mm，Y方向位移最大值为靠近坝踵的坝腹部位，为4.41 mm。

坝体第一主应力见图4。由图4可知，在水荷载及坝体自重作用下，X方向上应力在坝踵与坝顶处较为集中，坝顶靠近坝体下游面处的应力较大，大坝坝体内X方向应力，由靠近坝踵的坝腹处向坝顶处逐渐变大；坝体竖直方向上的应力从坝体上游面向下游面呈等压线向下分布，逐渐减小，垂直方向上坝踵处应力也较为集中。

图3 坝体位移云图

从坝体静力分析结果，第一主应力分布图可见，其最大受力处在坝踵，相较于坝体其他部位，其受力较集中，尤其大坝坝踵处与水压接合面以及基岩结合面处的受力是最大的，应该加强该处的补强加固，同时此处也是容易产生滑移变形的重要原因。

图4 坝体应力云图

2.2 变形及强度验算

坝体静力计算结果见表1。

表1 坝体静力计算结果

由表1可知，重力坝X与Y方向位移最大值分别为12.12 mm和4.41 mm。由重力坝变形要求可以得出，最大的变形量为L/650 mm，其中L为坝高，本文取120 m，最大变形量即为184.615 mm[2]

坝体静力分析以第一主应力为主，其最大压应力为2.56 MPa，最大拉应力为0.28 MPa。根据《混凝土结构设计规范》强度要求可知，C40混凝土的抗拉强度与抗压强度设计值分别为1.70 MPa和19.0 MPa,故从强度的角度来看，该重力坝满足强度设计要求[3-5]。

3 反应谱法在ANSYS中的实现

3.1 模态分析

3.1.1 各阶振型及频率计算

首先进行坝体模态分析，用于得到其振动特征(即所研究坝体的固有振型和频率)，它们是坝体地震动力分析中的重要参数，也是接下来进行谱分析的基础。

在水深h处的地震动水压力值，根据公式(6)视为相应的坝面附加质量。

(6)

式中：PW(h)为水深为h处作用在迎水坝面上的动水压力值；h为水深,m；ah表示地震时水平向加速度代表值，当地震烈度为8°时ah=0.2g；ρW为水体质量密度的标准值,ρW=1 g/cm3；H0为水的总深度,m。

3.1.2 反应谱谱值计算

图5为坝体标准设计反应谱曲线图[7]，由图5可得反应谱曲线方程如下：

(7)

式中：T为体系自振周期，s；T0为特征周期,s；β表示加速度反应谱标准值,Hz；βmax设计反应谱最大值,Hz。

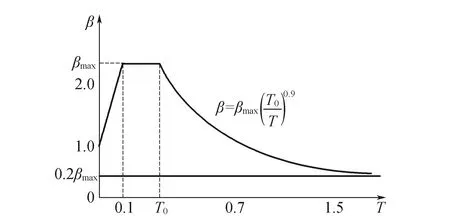
图5 大坝设计反应谱

由于是混凝土重力坝地震动力分析，因此本文最大反应谱值βmax的取值为2，根据《水工建筑物抗震设计规范》，本文中水工建筑物场地类别为I等，故特征周期T0的取值为0.2 s[4]。

完成坝体模态分析的求解之后，根据模态分析结果前18阶频率值f，可以算出对应的周期T，再根据大坝反应谱曲线方程(式7)，可以计算出前18阶的反应谱值，见表2。

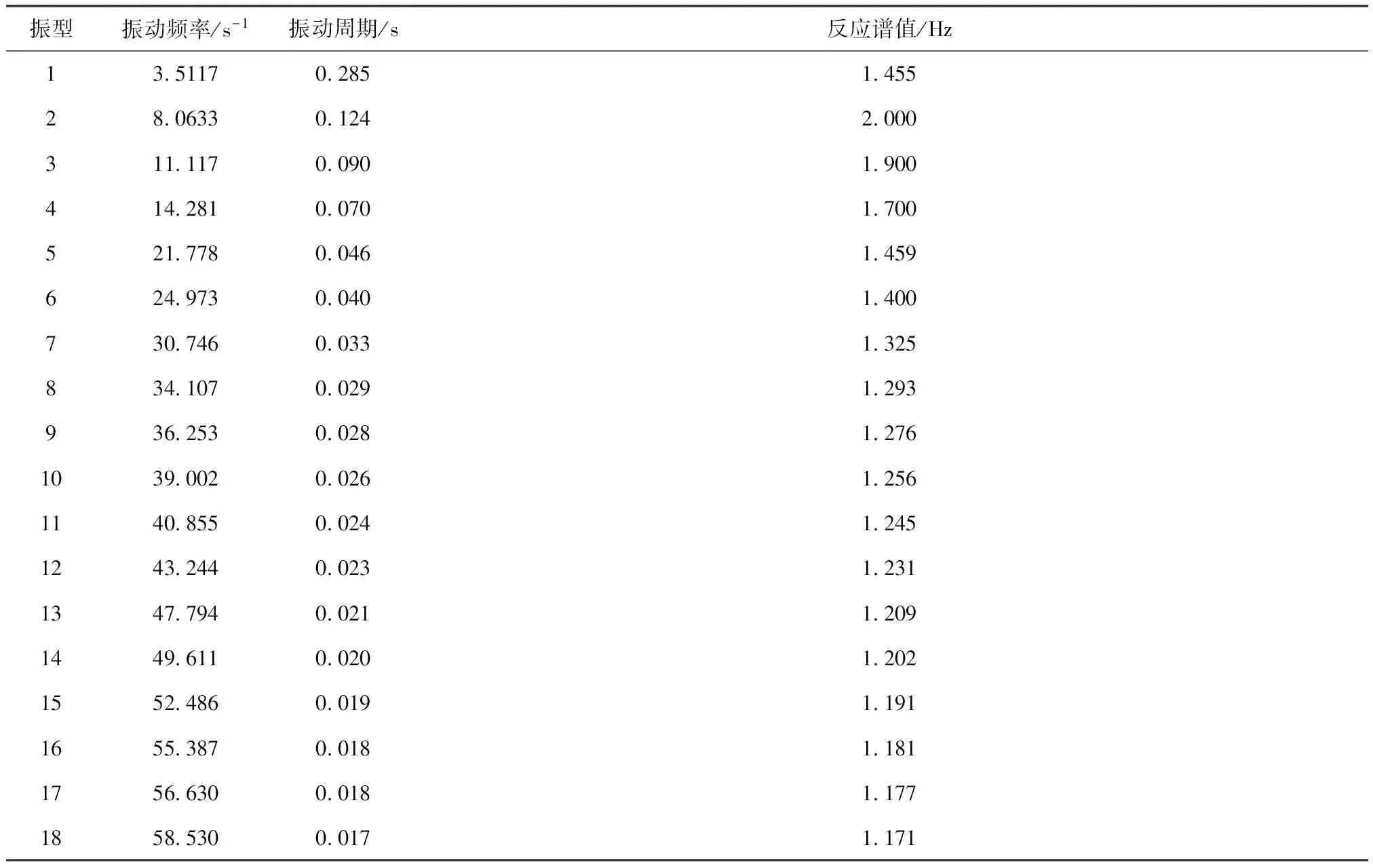
表2 大坝振动频率及反应谱值

3.2 反应谱分析及模态扩展

为将模态提取方法得到的完整振型写入结果文件中，接下来进行谱分析及模态扩展，将模态分析结果和已知谱联系起来计算结构响应，用于分析随机荷载作用下结构的动力响应情况。

将地震作用下模态分析得出的坝体各阶频率和反应谱谱值输入，进行反应谱分析，并进行18阶模态扩展，得出各阶反应谱分析结果。设置分析类型为反应谱分析：Antype,Spectr。

设置地震作用方向：SEDX,SEDY,SEDZ；其中X，Y，Z为分析开关，考虑该方向的地震作用时设置为1，不考虑该方向地震作用时设置为0。本文仅考虑竖向地震作用，即SEDY=0。

输入各阶频率：Freq,f1,f2,…… ,f9;Freq,f18；其中f1～ f18为坝体第1～18阶频率。

输入各阶频率所对应的反应谱谱值：Sv,0.05,d1,d2,…… ,d9;Sv,0.05,d18，其中d1～d18为坝体第1～18阶反应谱谱值。进行模态扩展：Expass,on;Mxpand,18, Yes,0.005[6]。

在经过模态分析与谱分析步骤后，需要将各阶振型的最大反应组合叠加求得结构的最大反应。由于各阶振型的最大反应不是同时发生的,因此不能通过简单的代数相加求得总的最大反应。本文采用平方和方根法，即取各阶振型地震作用效应的平方和，再取其方根作为总的地震作用效应，即：

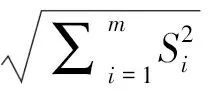
(8)

式中：S为总地震效应(即坝体的动应力)，MPa；Si为第i阶振型的效应(第i阶振型地震荷载产生的动应力)，MPa；m为所提取振型的最大阶数。

3.3 计算结果分析

通过坝体的地震动力分析可见坝体整体变形逐渐增大，从第1～18阶，坝体形态变化很大，且坝体有效挡水高度也明显降低。

反应谱分析是在一定频率范围内实施的，而坝体的结构动力特性随着频率的变化而变化，因此在模态分析完成后，还要进行模态合并求解，才能得到坝体结构随频率变化真实的位移与应力响应。完成合并模态求解过程后，得到坝体随各阶频率变化的真实位移及应力云图，选取若干具有代表性的位移云图见图6。

坝体随各阶振型的不断变化，X方向位移、Y方向位移及最大位移数值见表3。

上文中已提到，坝体最大变形量允许值为184.615 mm。故该坝体X方向最大位移(第2阶位移1.40 mm)，Y方向最大位移(第6阶位移0.926 mm)，最大位移(第2阶位移1.46 mm)，均满足坝体变形要求。

由于本文主要考虑坝体第一主应力，故选取若干具有代表性的第一主应力云图见图7。

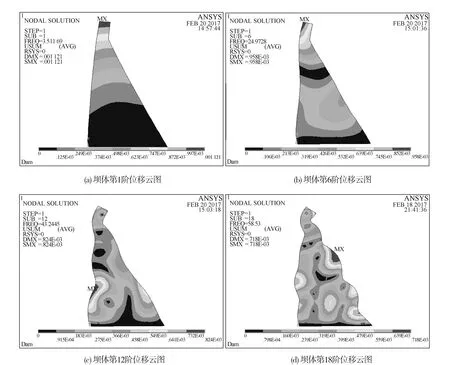
图6 坝体位移云图

振型X方向最大位移/mmY方向最大位移/mm最大位移/mm110900272112021400041814603000706540737412400507134051070034914006023409260958709670482124780359047405539064202340668振型X方向最大位移/mmY方向最大位移/mm最大位移/mm100690092411531105930920104012061307930824130673076808331404050756087215068003860756160567085110201702340815081718032408601044

图7 各阶第一主应力云图

各阶振型所对应的压应力与拉应力的数值见表4。

表4 各阶拉压应力变化值

由表4可见，坝体最大拉应力为0.320 MPa，发生在第18阶振型时；最大压应力为2.70 MPa，发生在第16阶振型时。上文中已提到，C40混凝土的抗拉强度设计值与抗压强度设计值分别为1.70 MPa和19.0 MPa，因此该坝体工程是满足设计强度要求的。

通过上述计算结果可知，地震时坝体的最大振幅通常出现在坝顶，动力放大作用很强，在坝顶断面突变处很容易产生水平裂缝。应采取降低坝顶荷载，增强坝顶结构刚度的工程措施。

4 结 论

本文为探究在地震荷载作用下混凝土重力坝坝体的应力及位移响应情况，首先对所选重力坝进行了无地震荷载作用的静力分析，得到坝体的应力场和位移场，从而对坝体的安全性能有所了解，得到在120 m高坝的正常蓄水工况下，坝体的强度及变形均满足要求的结论。然后选取坝体非溢流断面进行地震动力分析，同样得到在地震荷载的作用下，大坝的应力及位移响应情况，结果均在控制范围以内，得出大坝在地震裂度为8°的地震荷载作用下，变形及强度均满足要求的结论。

由于最大位移及最大应力、应变主要集中于大坝的中上部、坝踵、坝趾、地基接触面、几何形状突变等局部位置。对坝体的受力不利，在设计和施工中应引起足够的重视。

[1] 马慧. 基于ANSYS的混凝土重力坝抗震优化设计研究[D]. 北京: 华北电力大学, 2014.

[2] 王金龙. 重力坝抗震性能有限元分析[J]. 潍坊学院学报, 2010,10(6):113-115.

[3] 隋红军. 基于ANSYS重力坝抗震性能分析[J]. 建筑技术开发, 2015,42(6):63-65.

[4] 中华人民共和国国家能源局.水电工程水工建筑物抗震设计规范：NB 35047-2015[S]. 北京: 中国电力出版社,2015.

[5] 中华人民共和国住房和城乡建设部，中华人民共和国国家质量监督检验检疫总局. 混凝土结构设计规范:GB 50010-2010[S]. 北京: 中国建筑工业出版社, 2010.

[6] 张传国. Ansys在混凝土重力坝振型分解反应谱分析中的应用[J]. 云南水力发电, 2009(6):24-27.

Application research of response spectrum analysis to seismic performance analysis of gravity dams

GONG Xun1,XIN Xin2, LI Meng2,DENG Yuan2,LI Youran2

(1.HuizhouHuayuwaterconservancyandHydropowerEngineeringSurveyDesignCo.,Ltd.，Huizhou516000,China；2.SchoolofWaterResourcesandEnvironment,ChinaThreeGorgesUniversity,Yichang443002,China)

In this paper, firstly,the static analysis was adopted:the PLANE182 element in ANSYS was used to calculate the stress and deformation of the dam under the action of dead weight and water pressure.Then, the seismic dynamic analysis of the dam body was carried out,it included extraction modal and determination of dam natural frequency and modal shape,and the spectral value of the reaction spectrum was obtained by using the response spectrum equation.Then, the response spectrum analysis and modal expansion were carried out, and finally the modal was merged.The modal in the dam body was obtained under the stress and displacement response.The results show that the seismic fortification intensity for 8 degrees, the deformation and strength of the dam used in this paper can meet the requirements.The maximum stress and strain are mainly concentrated in the middle and upper parts of the dam, the heel of the dam and the toe of the dam,attention should be paid to the design and construction in the future.

seismic performance; response spectrum; modal analysis; PLANE182 element; seismic fortification intensity

国家自然科学基金青年科学基金(51109134);三峡大学研究生科研创新基金(SDYC2016004)

龚 勋(1986-)，男，湖北鄂州人，助理工程师，主要从事农业水文方面的研究工作。E-mail：20757783@qq.com。

TV642.3

A

2096-0506(2017)10-0001-07