重力梯度力矩近似公式适用条件的探讨1)

谭述君 殷伟栋 穆瑞楠 ,†(大连理工大学航空航天学院，辽宁大连116024)

†(大连理工大学工业装备结构分析国家重点实验室，辽宁大连116024)

重力梯度力矩近似公式适用条件的探讨1)

谭述君∗,†,2)殷伟栋∗穆瑞楠∗,†∗(大连理工大学航空航天学院，辽宁大连116024)

†(大连理工大学工业装备结构分析国家重点实验室，辽宁大连116024)

教材中重力梯度力矩经典近似公式是基于常规尺寸空间结构推导的，如果直接应用于超大尺寸结构可能会导致精度不够、甚至错误的结果.以超大空间哑铃结构为研究对象，对比了基于重力梯度力矩非近似公式与经典近似公式得到的姿态动力学响应，指出了经典近似公式的局限性.通过提高重力梯度力矩中近似项的保留精度，提出了修正公式，并验证了该公式的适用性.所得结论是对重力梯度力矩教学内容的有益扩展，对工程应用也有帮助.

姿态动力学，超大尺寸空间结构，重力梯度力矩,经典近似公式，适用条件

随着需求增长以及技术的积累，当今航天器发展迅速，朝着大型化和复杂化发展.如空间太阳能电站[1]这类超大尺寸空间结构，其聚光系统的尺度往往达到千米量级，因此有必要开展针对超大空间结构的理论研究.由于航天器各个部分的质量微元到地心的距离有微小差别，使合力有时不通过航天器质心，从而产生扰动力矩，称为重力梯度力矩[23]，这种扰动力矩是影响航天器姿态运动的重要因素之一[4].

由于重力梯度力矩计算公式相当复杂，为了工程上实用，相关教材中都给出了重力梯度力矩的经典近似公式[25].这种公式是基于常规尺寸空间结构推导的，但教材中往往缺少明确的说明，这可能使学生误认为经典近似公式可直接应用于超大尺寸空间结构的研究工作.本文以超大空间哑铃结构为研究对象，分别推导哑铃重力梯度力矩的非近似公式和经典近似公式，通过两者姿态动力学响应的对比，分析经典近似公式的应用条件.通过提高重力梯度力矩中Taylor级数展开的保留精度，提出修正的近似公式，并验证新公式的适用性.

1 重力梯度力矩的经典近似公式

空间哑铃模型是重力梯度相关研究工作中常用的简化模型，这类模型建模简单，且具有明显的质量分布特性[56].针对哑铃模型在轨道平面内的姿态运动，推导重力梯度力矩的经典近似公式.图1包含了哑铃结构AB和中心引力体E.其中哑铃中间连接部分质量忽略且不可伸长，长度为x，在其两端点A和B上的集中质量分别为m1和m2，其质心位置处的轨道半径为R.两端点A和B到中心引力体E的距离分别为r1和r2，到哑铃质心O的距离分别为x1和x2.姿态角ϕ为Ox轴与质心处轨道半径方向的夹角，姿态运动以逆时针方向为正方向.

图1 空间哑铃模型

根据重力梯度力矩公式[2]，该哑铃结构的重力梯度力矩精确表达式为

其中,m=m1+m2,x=x1+x2,µ=GMe是引力常量，G为万有引力常数，Me是地球质量；其中

为了简化公式，教材[25]中将式(2)和式(3)均以Taylor级数的形式展开，并只保留x/R的一次项精度，这里包含了尺寸假设条件R≫x，得到表达式为

将式(4)和式(5)代入式(1)，即可得到重力梯度力矩经典近似公式

由动量矩定理˙h=M得姿态动力学方程为

将式(1)代入式(7)得到哑铃结构的非近似姿态动力学方程[6]

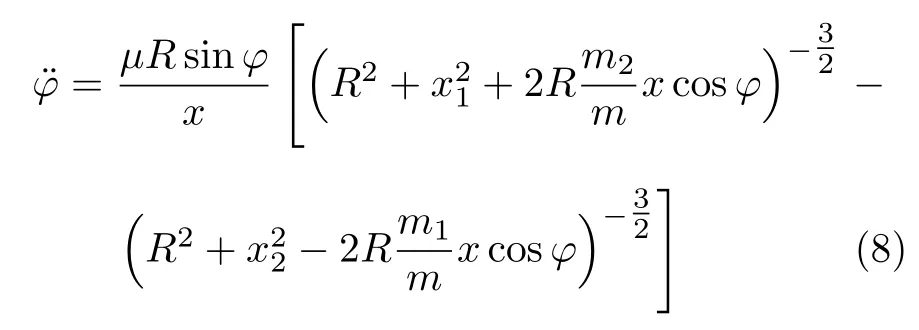
而将式(4)代入式(7)得到基于经典近似公式的哑铃姿态动力学方程

与非近似姿态动力学方程相比，该方程没有包含尺寸和质量等参数，因此无法反映这些参数对姿态运动的影响.对于小尺寸结构，这些参数的影响可以忽略.但随着尺寸增大，仍忽略这些参数的影响则可能导致精度不高、甚至错误的结果.

2 经典近似公式的适用条件

本节通过与非近似姿态动力学方程对比仿真结果，说明在超大尺寸空间结构的姿态动力学问题中经典近似公式的应用范围.重力梯度力矩作用下哑铃结构姿态响应的仿真参数设置：地心引力常数 µ为 1.4352×109km3/min2；轨道高度为 200km(低轨道)，则哑铃模型质心轨道半径R为6574.33km；哑铃A端质量m1为1000kg，B端质量m2为0.1kg，总质量m为两端质量之和；哑铃尺寸x为10km；初始姿态角速度为 0.仿真步长为0.1min，总仿真时长为 1000 min，求解精度为 1×10−9rad.

当哑铃结构的初始姿态角较小时，取初始姿态角为0.1rad时，图2给出了基于经典近似公式和基于非近似公式得到的姿态角响应曲线及其差值.可以看出,在大尺寸结构下，在结构质量分布不对称，两者响应误差约为0.02rad，此时存在大于10%的相对误差.因此对于超大空间结构，当结构质量不对称分布时，在小初始姿态角下基于经典近似公式的姿态角响应结果存在较大的误差，经典近似公式在该情况下不适用.

图2 姿态角对比及误差曲线(ϕ0=0.1rad)

当哑铃结构初始姿态位于不稳定平衡点，即初始姿态角为π/2的位置时，图3给出了基于经典近似公式与非近似公式的姿态角响应曲线，可以明显发现两者初始姿态转动方向相反.哑铃在不稳定平衡点时，由于两端质量不同，重力梯度应使质量较大的一端 (m1)靠近地心 (顺时针转动)，这与非近似公式的结果一致.而由经典近似公式却得出哑铃发生逆时针转动，与真实姿态运动过程相违.分析方程(9)可知，由于经典近似公式得到的姿态动力学方程中没有质量参数，因此无法体现重力梯度力矩对姿态运动的影响.因此，对于大尺寸空间结构，质量非对称分布以及初始姿态位于不稳定平衡点时，经典近似公式不适用.

图3 姿态角对比曲线(ϕ=π/2)

3 修正近似公式及适用性的验证

通过增加式(2)和式(3)中的Taylor级数展开项数，建立重力梯度力矩修正近似公式.式(2)和式(3)的Taylor级数展开式重新写为

将式 (10)和式 (11)代入式 (1)得到重力梯度力矩的修正近似公式为

将式(12)代入式(7)得到修正后姿态动力学方程

可以发现，相比于式(8)，基于修正近似公式的姿态动力学方程 (13)包含了尺寸x以及两端质量m1和 m2参数，这些参数将对姿态运动产生影响.特别注意到，当 m1和 m2相等时，修正近似公式(12)与经典近似公式(6)是完全一致的.

利用上一节仿真参数和方程(13)进行分析，图4给出了初始姿态角为0.1rad时，基于修正近似公式与经典近似公式的误差曲线.可以发现，结构质量非对称分布时，修正近似公式误差远低于经典近似模型误差，其模型精度大大提高.当初始姿态角为π/2时，图5给出了基于修正近似公式与非近似公式的比较，可以看出此时修正近似公式能够得到与非近似公式近似一致的姿态响应，因此该公式适用于初始姿态角为π/2且质量非对称分布情况.

图4 经典近似公式与修正近似公式的误差曲线

图5 姿态角对比及误差曲线

4 结论

以空间哑铃模型为研究对象，通过对比基于重力梯度力矩非近似公式和经典近似公式的姿态动力学方程发现,后者没有包含结构尺寸和质量等参数.仿真结果显示，对于超大尺寸空间哑铃结构，基于经典近似公式得到的姿态角响应在小初始姿态角条件下的误差接近 20%，而在不稳定平衡点处时，其姿态角响应变化趋势与实际过程相反，由此说明了在超大尺寸空间结构的建模分析中，重力梯度力矩经典近似公式的使用存在限制条件.通过增加重力梯度力矩中近似项-Taylor级数展开的保留阶次，得到了重力梯度力矩的修正近似公式，并通过数值仿真验证了该公式的适用性.因此，建议在重力梯度力矩的相关教学内容中，应说明经典近似公式直接应用于超大尺寸空间结构的局限性，并介绍其修正思路，使学生对知识有更好的理解.

1 Glaser PE.Power from the sun:Its future.Science,1968,162(3856):857-861

2 刘暾,赵钧.空间飞行器动力学.哈尔滨：哈尔滨工业大学出版社,2003

3 张嘉钟,魏英杰,曹伟.飞行器动力学与控制.哈尔滨：哈尔滨工业大学出版社,2011

4 屠善澄.卫星姿态动力学与控制.北京：中国宇航出版社,1999

5 耿长福.航天器动力学.北京：中国科学技术出版社,2006

6 Malla RB.Structural and orbital conditions on response of large space structures.Journal of Aerospace Engineering,1993,6(2):115-132

V11

A

10.6052/1000-0879-17-063

2017-02-28收到第1稿，2017-04-01收到修改稿.

1)国家自然科学基金资助项目(11572069,11432010,11502040).

2)谭述君，博士，副教授，研究方向为航天器动力学与控制、空间智能结构分析设计与控制、运载火箭耦合动力学与控制、最优控制理论算法与应用.E-mail:tansj@dlut.edu.cn

谭述君,殷伟栋,穆瑞楠.重力梯度力矩近似公式适用条件的探讨.力学与实践,2017,39(5):496-499

Tan Shujun,Yin Weidong,Mu Ruinan.Application scopes of the classical approximate formula of the gravity gradient torque.Mechanics in Engineering,2017,39(5):496-499

(责任编辑:胡 漫)