一道力学竞赛题的多种解法及其相关问题讨论
李道奎 肖万伸 任毅如 李家文(国防科技大学航天科学与工程学院,长沙410073)(湖南大学机械与运载工程学院,长沙410082)
一道力学竞赛题的多种解法及其相关问题讨论
李道奎∗,1)肖万伸†,2)任毅如†李家文∗∗(国防科技大学航天科学与工程学院,长沙410073)†(湖南大学机械与运载工程学院,长沙410082)
分析了第十一届全国周培源大学生力学竞赛初赛试题中第13题的圆环受力与变形的特殊性,明确了题中圆环发生大位移小变形,给出了其多种解法,指出了原型题解答对读者的误导,并对大位移的影响、功与能的计算方法、中性轴的位置、应力应变分布等相关问题进行了分析与讨论,得到了圆环内部受力与变形的过程.
力学竞赛,分析法,能量法,中性轴
1 问题的提出
2017年第十一届全国周培源大学生力学竞赛初赛试题的第 13题(以下称本题)[1]为:图 1所示的圆环杆,材料的弹性模量为E,受集度为m、矢量方向与环杆轴线相切的均布力偶载荷,变形时杆件始终保持弹性状态,且横截面符合平面假设.环杆轴线半径为R,横截面(如图中A−A截面)为圆,其半径为r,试求
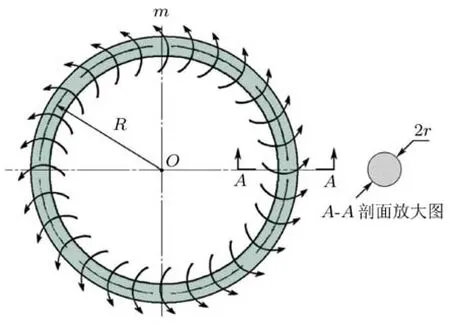
图1
(1)横截面上的内力;
(2)横截面的转角ϕ;
(3)横截面上内力的最大值.
提示:当X/Y≪1时,可做简化Y+X≈Y.
本题的原型为文献[2]中521页的11-24(以下称原型题),但原型题中仅需计算均布力偶与横截面的转角之间的关系(原型题外载荷方向相反,但不影响结果).文献[2]548-550页给出解答中,从垂直圆环轴线平面的某一对称面将其截开,根据对称性,认为横截面上只有对z轴的弯矩Mz,如图2所示.由平衡条件可得

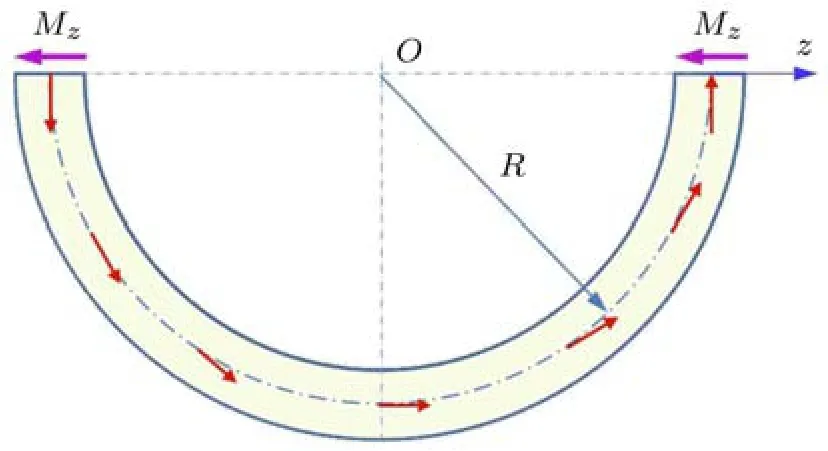
图2
文献 [2]给出的解答,对于解决原型题中的问题,是没有错的 (原因在下面会解释),但却会误导读者对整个题目的理解,即认为圆环横截面上的内力只有弯矩Mz,进而在求解本题时就会出错,特别是读者如果在此基础上采用能量法进行计算,则会得出错误的结论.下面将给出本题详细求解过程以及第2问的多种解法,包括分析法和能量法,并对题目和解答中涉及相关问题进行分析与讨论.
2 本题的分析法求解
因为根据对称性和受力特点,圆环任一横截面上的内力不仅有弯矩Mz,还有弯矩My(设其沿y轴正方向),其他内力分量为零,如图 3所示 (注意,图中的横截面是图2中右边截面).
考虑图3中横截面上任一点A(ρ,θ),通过该点的圆环周线长度为 lA=2π(R+ρcosθ).当横截面绕圆环轴线转过角度ϕ时,根据横截面符合平面假设可知,A点将移动到B点,如图3所示,圆环周线长度变为 lB=2π[R+ρcos(θ+ϕ)].点 A 的环向正应变为
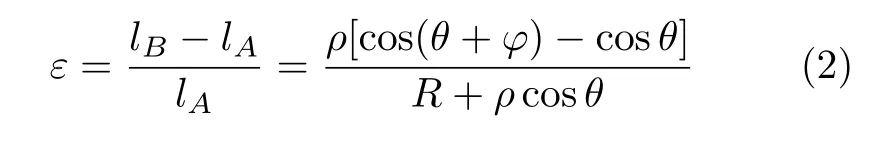
考虑到ρcosθ≪R,式(2)可简化为
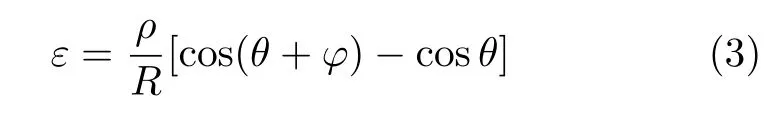
根据胡克定律,并结合式(3)可得
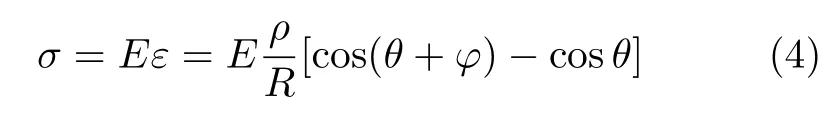
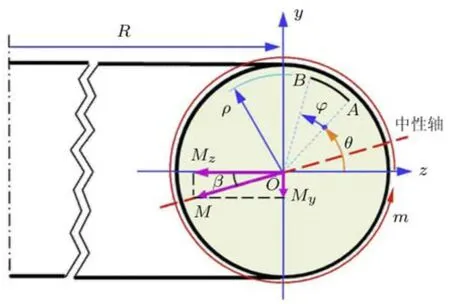
图3
根据横截面上应力形成的分布内力系与内力之间静力平衡关系,可得
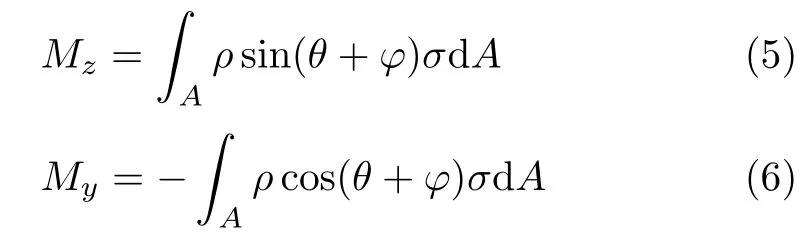
将式(4)代入式(5),积分可得
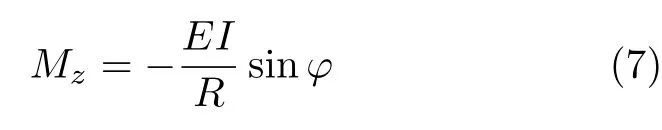
将式(1)代入式(7)可得
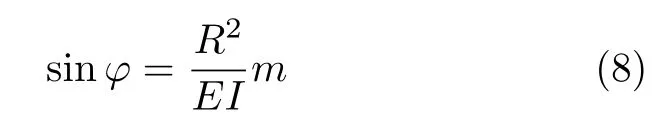
式(8)给出了均布的力偶载荷m与横截面的转角ϕ之间的关系,得到这一关系时并不需要考虑是否存在My,因此可以确定文献[2]给出的原型解答,是没有问题的.
将式(4)代入式(6),积分可得
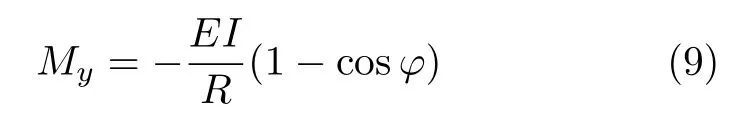
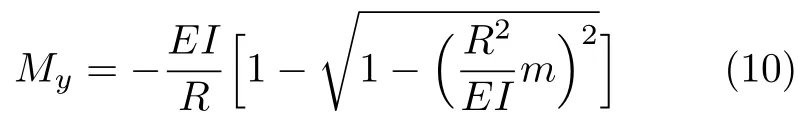
式(1)和式(10)就给出了横截面上的内力分量Mz和My的表达式,式中负号代表实际弯矩指向相应轴的负方向,如图3所示.其他内力分量为零,此即本题第1问的解答.
由式(8)可得
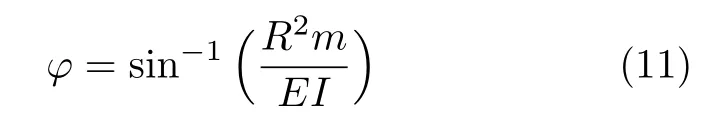
即本题第2问的解答.
利用式 (7)和式(9)可以算出横截面上的合弯矩为
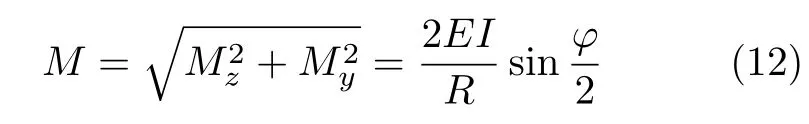
可见,当ϕ=π时,截面内力达到最大值,即
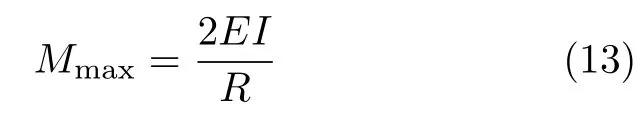
即本题第3问的解答.
3 本题第2问的能量法求解
在利用能量法求解时,均须计算构件内部储存的应变能.因此,先计算横截面的转角为ϕ时,圆环内部储存的应变能.由于每个横截面与同一圆环周线相交各点的应变能密度vε相同,因此,圆环储存的应变能为
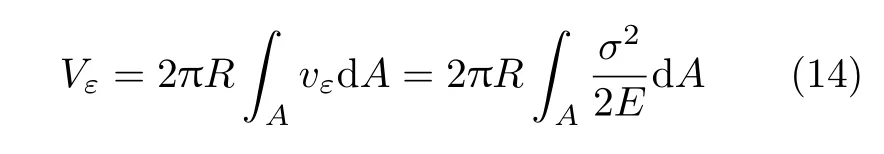
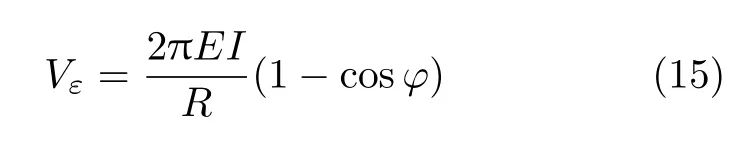
下面分别利用功能原理、卡氏第一定理和最小势能原理三种能量方法推导式(8),由式(8)很容易得到式(11),因此,在得到式(8)后就可认为本题的第2问得到了求解.
3.1 直接利用功能原理求解
设圆环横截面在分布力偶外载荷作用下,横截面的转角ξ由0缓慢变化到ϕ,此过程中外力所做的功为
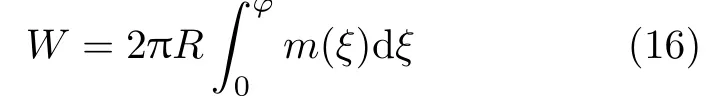
将式(15)和式(16)代入功能原理,即W=Vε,得
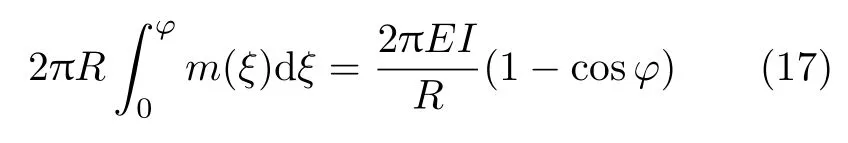
式(17)两端对ϕ求导,得到的结果与式(8)一致.
3.2 利用卡氏第一定理求解
由于圆环每个横截面形状与尺寸相同,应力分布也相同,因此沿圆环轴线单位长度内储存的应变能V.ε也相等,从而可得
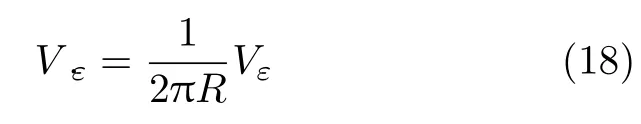
将式(15)代入式(18)可得
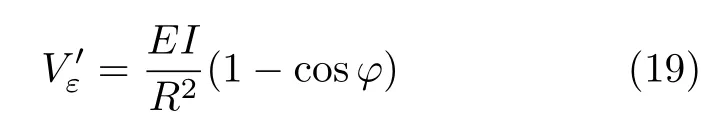
由卡氏第一定理,可得均布力偶载荷的集度(即沿圆环轴线单位长度均布力偶载荷的大小)为

将式(19)代入式(20),得到的结果也与式(8)一致.
3.3 利用最小势能原理求解
圆环在外力作用下的总势能等于应变能与外力功势能之和,即

式中,外力势能Vp为
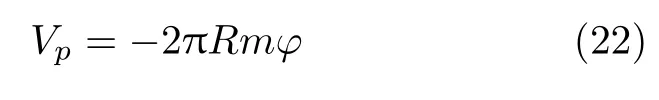
将式(15)和式(22)代入式(21),可得
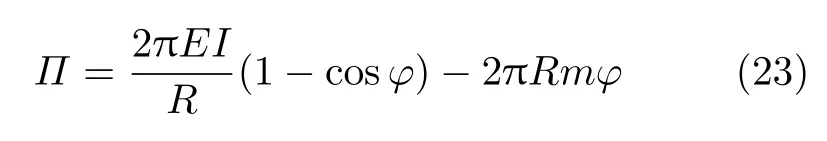
由最小势能原理
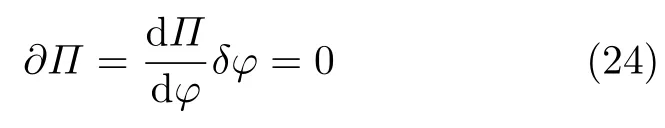
将式(23)代入式(24),同样可以得到式(8).
4 相关问题讨论
4.1 大位移的影响
由于位移(角位移ϕ)较大,在列截面分布内力系与内力之间的静力关系时,要考虑大位移引起的横截面内各点位置的变化.即在式 (5)中计算 Mz和式(6)中计算My时,微元面积dA上的微内力到z轴和y轴的距离,分别由ρsinθ和ρcosθ变为ρsin(θ+ϕ)和 ρcos(θ+ϕ).
4.2 功与能的计算方法
本题中外载荷为均布力偶载荷m,其相应位移为横截面的转角ϕ,它们之间并不成线性关系,而是成式(8)或式(11)描述的非线性关系,因此外力功不能采用 W=πRmϕ来计算,而只能采用积分形式即式(16)来计算;但外力势能并不受外载荷与相应位移之间关系的影响,依然可以采用式(22)来计算.
本题中圆环的变形比较特殊,尽管位移较大,但受各横截面之间的相互约束,变形(应变)较小,材料依然处于线弹性状态,满足胡克定律,可采用计算应变能密度,进而通过在整个体积上积分得到圆环内储存的应变能.当然,也可利用来计算应变能,但弯矩M 一定为横截面内的合弯矩,如果像原型题那样仅考虑Mz,则必然会得到错误的结论.
4.3 中性轴的位置
本题由于圆环的变形比较特殊,而且位移又较大,使得变形过程中横截面中性轴的位置也有其特殊性.
对式(3)和式(4)中的三角函数进行和差化积,得到
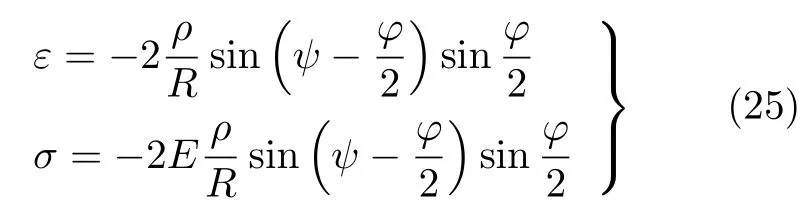
式中,ψ=θ+ϕ为截面上任一点 A(ρ,θ)在变形后的新位置的极角.
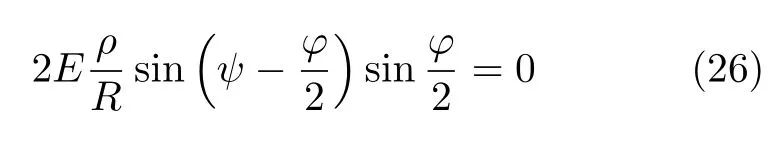
令式(25)中的正应力为零,得到当圆环发生变形时,0<ϕ≤π,由式(26)必然要求根据题目的物理含义,取n=0,可得中性轴为

式(27)代表的横截面内通过截面形心的一条直线,如图3所示.在横截面转角从0增大到ϕ ϕ的过程中,中性轴的位置离开z轴从0增大到 2.
4.4 应力应变分布
设横截面上的合弯矩与z轴负方向成夹角β,如图3所示,则由式(7)和式(9)可以得到
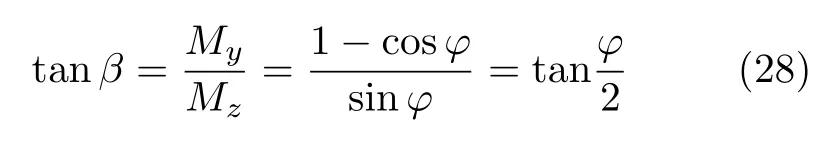
同时,式(25)给出了圆环横截面上任一点在某一给定横‡截面转·角ϕ下的环向正应变与正应力,其中,ρsinψ− 为该点到中性轴的距离(此处的距离为带正负号的距离),而其余各项与该点在截面内的位置无关,因此,圆环横截面上任一点处的环向正应变、正应力与该点到中性轴的距离成正比.
5 结论
本文给出了第十一届全国周培源大学生力学竞赛初赛试题中第13题的多种解法,并对大位移的影响、功与能的计算方法、中性轴的位置、应力应变分布等相关问题进行了分析与讨论,得到以下结论:
(1)本题可以有分析法和能量法等多种解法,但要注意对圆环的变形、横截面上的内力和应力进行较为准确的分析,特别需要考虑大位移引起的截面上各点位置变化.另外,原型题解答认为在圆环横截面上只有弯矩Mz是错误的.
(3)本题中的圆环在m作用下,发生大位移小变形,内部受力与变形过程是这样的:横截面在m的作用下发生绕形心的旋转,截面中性轴通过截面形心,且从z轴开始绕着截面形心逆时针旋转,在横截面转角从0增大到ϕϕ的过程中,中性轴的位置离开z轴从0增大到 2,截面内的合弯矩矢量方向与中性轴在同一条直线上,各点的应力、应变与该点到中性轴的距离成正比.
1 竞赛组委会.第十一届全国周培源大学生力学竞赛初赛试题.www.cstam.org.cn
2 张行编著.材料力学分析方法.国防工业出版社,1988
“第八届全国力学史与方法论学术研讨会(HMM-VIII)暨全国力学学术大会力学史与方法论分会场”学术活动纪要
“第八届全国力学史与方法论学术研讨会(HMM-VIII)暨全国力学学术大会力学史与方法论分会场”于2017年8月13-16日在北京召开.本次会议由中国力学学会力学史与方法论专业委员会主办,北京大学工学院承办.整个活动分两个阶段进行:第一阶段:13日下午,在北京大学工学院开幕,中国力学学会力学史与方法论专业委员会主任委员郑晓静院士致开幕词,随后进行特邀报告;第二阶段:在力学大会作为分会场,分别于15日上午及 16日上午在国家会议中心进行学术交流,其中16日为两个平行分组报告,有近40名专家学者与会报告.
会议还吸引了来自全国众多单位的力学界资深教授、活跃在力学科研与教学第一线的中青年教师以及力学专业研究生参加,成为学术氛围最热烈的分会场之一.
在学术交流过程中,17位力学前辈做了精彩纷呈的大会邀请报告:武际可教授指出力学几何化具有重要意义,并介绍了黎曼几何、辛几何以及对偶等概念在力学中的应用,尤其指出目前力学专业教学需提高对微分几何等数学知识的重视;王大钧教授在身体不适的情况下还坚持做报告,和大家分享了他对结构力学定性理论研究方法和科学美的感悟;王敏中教授身体力行华罗庚先生名言 “弄斧到班门,耍刀在关庙”,风趣地回忆了他与9组力学高手“过招”的佚事;余寿文教授讨论了固体力学间断问题的研究方法,指出间断区域应受到关注,重点介绍了“放大镜”和“均匀连续化”两种极为有用的方法;徐秉业教授探讨塑性力学的教学方法和塑性力学常用的研究方法;朱克勤教授以俄罗斯科学院为主线,回顾了俄罗斯和前苏联力学学科发展以及欧拉、伯努利、朗道、柯尔莫哥洛夫等力学家的成长之路;隋允康教授深情追思恩师钱令希先生,回顾了钱先生在科学研究、学科建设、教育教学、人才培养和大学管理五个方面的重要贡献;钟万勰院士分享了对浅水波机械激波的深刻理解;姜锡权教授以分离式霍普金森杆和轻气炮为例,介绍了材料动态力学实验技术的发展史;王振东教授首先回忆了与周培源先生交往的故事以及全国大学生周培源力学竞赛的历史,接着通过泰勒、冯诺依曼和谢多夫估算原子弹爆炸当量的故事,说明量纲分析方法的强大能力;刘延柱教授回顾了德国工程力学大师马格努斯的生平以及在刚体动力学、陀螺力学、多体系统动力学等领域的重要贡献;程昌钧教授详细介绍了钱伟长先生博士论文 “薄壳和薄板的内禀理论”的主要内容和所获得的重要成就;嵇醒教授的报告认为弹塑性应力强度因子并不存在,以及他对这一问题的最新研究成果(因身体原因,嵇醒教授临时未能成行,由同济大学朱峰博士代为报告);戴世强教授从两本力学科普著作《院士谈力学》和《流体力学通论》谈起,阐释了全景式力学科普书籍在力学通识教育中具有不可多得的作用;余同希教授从力学的多个分支方向讨论了如何确定撞击力的问题;吴昌华教授叙述了物理学各种基本粒子的发现历史;张鸿庆教授阐释了他关于不同文化及其在数学力学中应用的理解.
在大会分组报告中,与会的中青年学者分别报告了各自的研究成果,内容涉及力学各分支学科的发展史、科研和教学方法论,部分高校和科研院所力学学科发展史、著名力学家的学术思想和贡献等.陈海波、段慧玲分别介绍了中国科技大学、北京大学力学学科的发展史与现状;王柏懿回顾了创建初期的中科院力学所和中国力学学会;白欣、杨绍琼、刘俊丽等报告了不同时期国内力学教育、研究、专业建设、著作和办刊等的研究成果;殷雅俊、龙运佳、游阳明、顾娟、糜长稳、王建祥等分享了对不同力学研究方法论的理解;叶红玲、董璐、张伟伟等介绍了各自在力学教学和课程建设中的宝贵经验.
最后,专业委员会主任郑晓静院士和党支部书记刘俊丽分别致辞,简要总结了本次会议,希望经过同仁们的共同努力,涌现出更多更深层次的研究成果,并期待两年后的重逢.
会议的组织工作得到了与会者的一致好评,大家对东道主北京大学工学院唐少强教授团队师生们为会议所做的大量细致而有效的会务工作、以及中国力学学会和力学大会组委会对本次研讨会的支持表示诚挚的谢意.
值得一提的是,本专业委员会长期形成的尊老携青的风尚不仅继续发扬而且不断加强,这次会议因作为中国力学大会分会场,考虑到退休老教授的经费困难,申请中国力学学会为七十岁以上的老先生免交注册费,而且北京大学工学院为外埠老先生们提供了很好的食宿与交通条件.
(中国力学学会力学史与方法论专业委员会供稿)
O3
A
10.6052/1000-0879-17-241
本文于2017-07-06收到.
1)李道奎,教授,主要从事结构设计与分析科学研究工作和材料力学教学工作.E-mail:lidaokui@nudt.edu.cn
2)肖万伸,教授,通讯作者,主要从事工程结构强度分析与固体力学教学工作.E-mail:xwshndc@163.com
李道奎,肖万伸,任毅如等.一道力学竞赛题的多种解法及其相关问题讨论.力学与实践,2017,39(5):544-547
Li Daokui,Xiao Wanshen,Ren Yiru,et al.Various solutions to a mechanical contest problem and the discussion on related problems.Mechanics in Engineering,2017,39(5):544-547
(责任编辑:周冬冬)

