基于遗传算法的自动组卷模型及改进研究
罗宇,罗曼,夏德奇
(中国气象局气象干部培训学院湖南分院,长沙410125)
基于遗传算法的自动组卷模型及改进研究
罗宇,罗曼,夏德奇
(中国气象局气象干部培训学院湖南分院,长沙410125)
针对标准遗传算法进化慢、易早熟等问题,建立多重约束目标组合优化模型,对编码策略、种群初始化和遗传算子进行改进。实验表明:相较于标准遗传算法,改进遗传算法可明显提升所得试卷的最大适应度(0.79提升至0.84)和平均适应度(0.74提升至0.83),改善早熟现象,提升算法执行速度。
0 引言
在气象教育培训领域,考试是培训过程中的重要环节。随着计算机辅助教学技术迅速发展,智能组卷已成为一项被广泛研究和实际应用的课题。如何综合考虑章节比例、题型比例、知识点覆盖、试卷难度及区分度等多重约束条件,生成一套能够评价学员知识和能力的试卷是组卷算法的核心问题。目前传统的组卷算法多为随机组卷算法[1-3]或回溯试探组卷算法[4-5]。由于此类算法中的组卷模型存在成功率低、算法结构复杂和组卷时间长等问题,不能很好满足目前试题资源日益增长现状。基于仿生的遗传算法(Generic Algo⁃rithm,GA)作为一种随机搜索算法,可在潜在的解决方案中逐步求得近似的全局最优解,其在组合优化问题求解领域得有较多应用[6-7]。在此基础上许多学者尝试利用遗传算法解决自动组卷问题,取得较好效果。相关研究表明,引入遗传算法可显著改善组卷效率和质量[8-11]。但由于其算法本身缺陷,可能导致组卷算法出现早熟、后期搜索效率低甚至组卷失败等问题[12]。
本文采用多重约束目标组合优化模型,对题型分布、难度系数、区分度、章节分值等约束条件进行量化,实现自动组卷问题数学建模。同时采用基于试卷的分组编码策略、均匀化初始种群和自适应遗传算子[13-14],改进标准遗传算法在自动组卷应用上的不足,实现算法优化。
1 自动组卷算法数学建模
自动组卷时,需从题库中抽取一组试题P,使其属性变量A(题型、难度、区分度、分值、所属章节及知识点等)在对应取值范围V内满足约束条件R,即将自动组卷抽象为多重约束目标组合优化问题。本文中选取知识点、难度、区分度和所属章节4个属性加以量化,并结合对应约束条件构造适应度函数。
知识点属性涉及试题的具体考核内容。令Ktotal为题库知识点总数,K为试卷中不重复知识点数量和,n为试卷中题目总数,定义知识点适应度函数:

难度属性反映试题难易程度,对应取值范围为[0,1]。对于客观性试题,难度计算方法为:

对于主观题,难度计算方法为:

其中,M为考生总数,mj为答对第j题人数,xij为第i位考生在第j题上的得分,wj为第j题的满分分值。令β为组卷期望难度,采用正态分布建立难度适应度函数:

区分度属性指试题对被试者情况的分辨能力的大小,反映试题区分不同水平受试者的程度,其计算方法为:

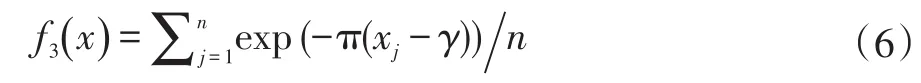
试题所属章节一般由考纲中各章节题目分值确定。假设题库中试题共涉及N个章节,考纲中各章节所占分值为Sj,组卷生成试卷中各章节分值为sj,其适应度函数可有正态分布建立:
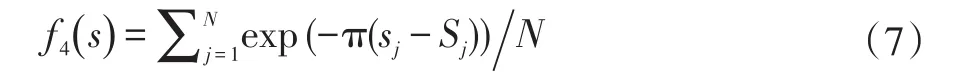
由上述定义的目标函数可知,自动组卷所得试卷的各项属性和属性的期望值偏差越小,所得目标函数值越大。因此组卷算法的多目标优化即在综合考虑知识点、难度、区分度和所属章节4个约束条件下,求得总的适应度函数:

其中wi为各属性适应度函数的权重,满足其具体取值,可根据不同考试需求进行设置。由各属性目标函数定义可知,F(x)∈(0 ,1),其取值越大意味着组卷生成的试卷质量越好。
2 算法设计
2.1 面向试卷的实数分段编码策略
编码策略是应用遗传算法时需解决的首要问题,也是设计遗传算法是的关键步骤之一。不同的编码方式会影响交叉、变异等遗传算子的运算方式,进而决定算法进化效率。在自动组卷应用中,标准遗传算法一般采用面向题库的二进制编码策略[9-10],即题库中某一题选中时表示为1,未选中表示为0。该编码策略操作简单、易于理解、搜索效率高,但在进化过程中,不易控制各题型的数量比例,导致组卷算法失败或过早收敛。且采用二进制编码策略时,组卷算法的搜索空间取决于题库大小,若题库较大,会导致搜索空间过大,极大影响进化后期搜索效率。
为解决上述不足,采用面向试卷的实数分段编码策略,将一份试卷映射成一条染色体,每一被选中的试题对应染色体上的一个基因,其编码直接利用其在题库中的编号表示。同时根据试卷对题型的要求,将染色体上基因分段,每段对应一类题型(图1)。考虑到同一题型试题分值一般相同,采用该编码策略可以很好满足试卷对总分和各题型数量的要求,简化约束条件和算法流程。基因段之间相互独立,确保初始化、交叉和变异等遗传操作在不同试卷的相同基因段内进行(图2,加粗边框内为交叉部分),保证进化所得的各染色体中各题型数量和总分正确匹配,避免非法解对算法搜索效率的影响。

图1 面向试卷的实数分段编码
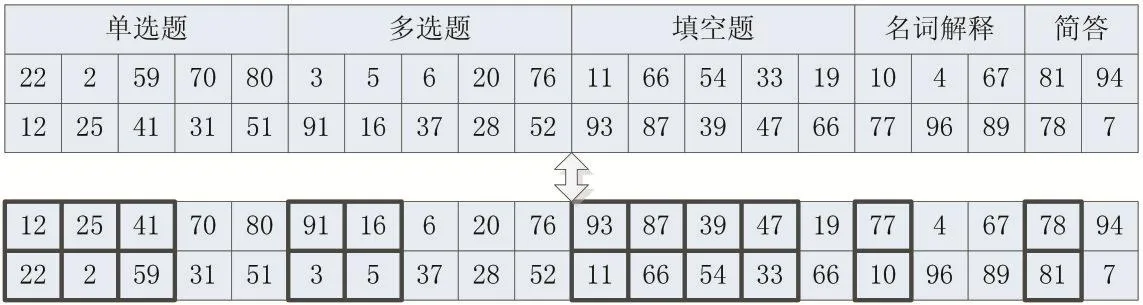
图2 不同试卷间的交叉操作
2.2 优化初始种群
初始种群的特性会明显影响算法结果和效率。标准遗传算法一般采用随机方法生成初始化群体,容易造成解空间过大,进化迭代次数过多,组卷结果较难把握。
针对上述问题,在面向试卷的实数分段编码策略基础上,采取不放回抽样方法使初始种群所处解空间尽量分散,并优化初始种群适应度。即对于大小为m的初始种群,随机产生n组染色体,计算各染色体总体适应度,保留适应度最大的作为初始染色体,并循环m次产生初始种群。该方法在不显著增加种群初始化复杂度的情况下可明显加快遗传算法收敛速度,减少迭代次数,增强进化效率。
2.3 自适应遗传算子
交叉和变异是遗传算法的重要步骤,交叉概率(Pc)和遗传概率(Pm)对算法性能有决定性影响[13-14]。标准遗传算法一般使用固定的Pc和Pm,以便在进化初期快速筛选掉适应度较差的个体,进而提升种群的平均适应度。但在进化后期,固定概率容易破化较优解,降低种群差异性,使算法陷入局部最优解,出现早熟现象。
为改善上述不足,在进化过程中采用自适应机制,根据各代的适应度情况,对Pc和Pm进行动态调整。对于适应度较高的个体,对应较低的Pc和Pm,使其更易进入下一代继续进化;对于适应度较低的个体,对应较高的Pc和Pm,使其更容易在交叉变异中重组基因,进而克服早熟,并提高搜索效率。自适应算子采用线性函数:
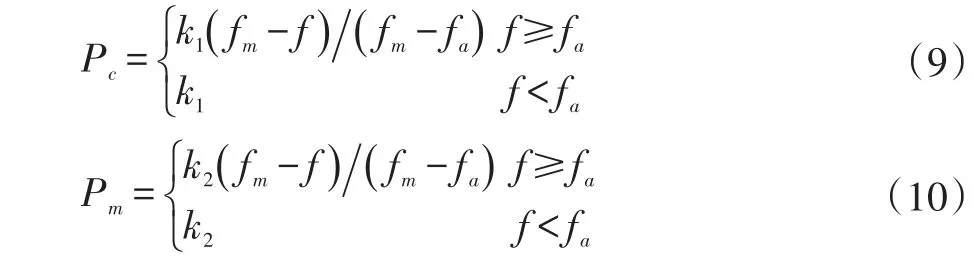
式中 f为个体适应度,fm和 fa分别为群体最大适应度和平均适应度,k1和k2为系数,可根据不同问题灵活取值。同时,为进一步加快算法收敛速度,在进化过程中用适应度最好的个体替换适应度最差个体,便于更优个体基因遗传到下一代。
3 实验与分析
参照《地面气象观测人员上岗资格考试大纲(2013)》,构造模拟题库对标准遗传算法(standard ge⁃netic algorithm,SGA)和改进遗传算法(improved genetic algorithm,IGA)进行实验。题库包括6章内容,涉及120个知识点,其中填空题1792道,单项选择题2145道,多项选择题670道,名词解释题112道,简答题156道。组卷要求:总分 100,各章分值为{8,14,50,10,10,8},各题型分值为{23,35,20,6,16};试卷难度 0.6,区分度0.6,知识点、难度、区分度和所属章节4个约束条件权重分别为{0.15,0.35,0.35,0.15}。标准遗传算法交叉概率为0.5,变异概率为0.005,自适应算子系数依次分别为0.5和0.005,初始种群规模为50,最大进化代数为500。标准遗传算法和改进遗传算法组卷最大适应度和平均适应度对比分别如图3和图4所示。由图可知,在初始种群相同,进化代数同为500的情况下,改进遗传算法最终所得最大适应度和平均适应度分别为0.85和0.83,均高于标准遗传算法(0.79和0.74),说明改进遗传算法不仅近似最优解优于标准遗传算法,且所得种群总体质量明显更优。同时,标准遗传算法进化速度相较改进遗传算法慢(表1),且在适应度达到某一局部最优解之后基本停止进化,陷入早熟。
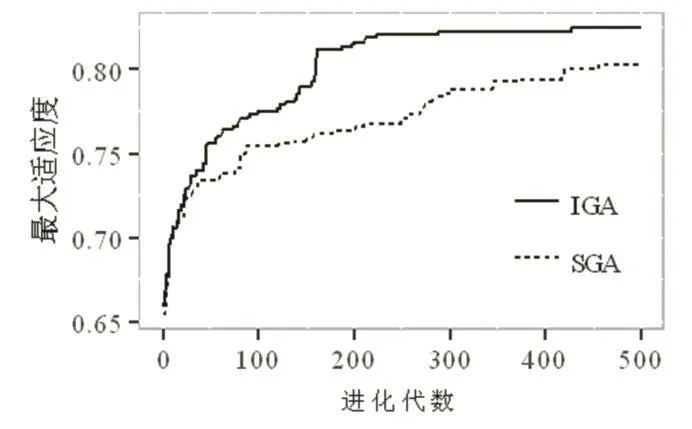
图3 SGA和IGA组卷最大适应度对比
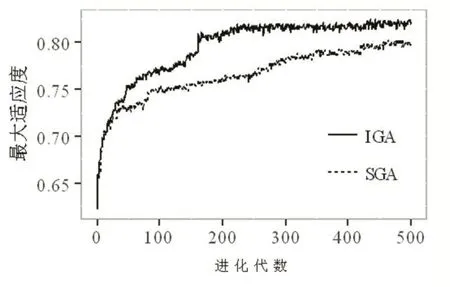
图4 SGA和IGA组卷平均适应度对比

表1 SGA和IGA不同进化代数时最大适应度对比
4 结语
针对标准遗传算法易早熟、收敛速度慢等不足,本文对组卷问题基于多重约束目标组合优化建模后,提出一种综合利用基于试卷的分组编码策略、均匀化初始种群和自适应遗传算子的改进遗传算法。实验表明,相较于标准遗传算法,改进遗传算法可明显改善组卷质量,克服早熟问题,提升搜索效率。目前该算法已应用于湖南省气象教育培训考试系统,体现出很好的稳定性和实用性。
[1]应继儒,胡立新,龙毅.试题库随机抽选数学模型的构建与实现[J].计算机应用,2000,20(1):46-47.
[2]王萌,金汉均,王晓荣.集合随机抽选法在智能组卷中的研究[J].计算机工程与设计,2006,27(19):3583-3585.
[3]谢深泉,胡宁静.数据库设计和自动组卷中的几个问题[J].湘潭大学自然科学学报,2002,24(3):27-31.
[4]李静梅,李静,焦平.一种可调整式的多元变量渐近寻优组卷策略[J].应用科技,2009,36(10):53-57.
[5]龚完全.基于最小回溯代价的只能组卷算法[D].湖南:湖南大学软件学院,2005.
[6]Xing Huanlai,Qu Rong.A Compact Genetic Algorithm for the Network Coding Based Resource Minimization Problem[J].Applied Intelligence,2012,36(4):809-823.
[7]Xing Huanlai,Qu Rong.A Nondominated Sorting Genetic Algorithm for Bi-Objective Network Coding Based Multicast Routing Problems[J].Information Sciences,2013,233(6):36-53.
[8]毛秉毅.基于遗传算法的智能组卷系统数据库结构的研究[J].计算机工程与应用,2003,28(6):230-232.
[9]李军.基于遗传算法的智能组卷系统研究[D].天津:天津大学,2008.
[10]梁兴建.程序设计类大学课程的智能组卷策略研究[D].成都:电子科技大学,2009.
[11]韦大欢.改进型遗传算法智能组卷系统的设计与实现[J].软件,2011,32(10):35-37,43.
[12]付旭辉,康玲.遗传算法的早熟问题探究[J].华中科技大学学报(自然科学版),2003,31(7):53-54.
[13]吴浩扬,朱长纯,常炳锅,等.基于种群过早收敛程度定量分析的改进自适应遗传算法[J].西安交通大学学报,1999,33(11):27-30.
[14]曲志坚,张先伟,曹雁锋,等.基于自适应机制的遗传算法研究[J].计算机应用研究,2015,32(11):3222-3225,3229.
罗宇(1984-),男,四川巴中人,工程师,硕士,研究方向为大气遥感与探测
罗曼(1986-),女,湖南长沙人,助理工程师,硕士,研究方向为气象教育培训技术
夏德奇(1965-),男,湖南邵阳人,副高级工程师,本科,研究方向为应用气象
2017-06-20
2017-10-10
Automatic Test Paper Generation;Genetic Algorithm;Multi-Objective Optimization;Adaptive
Research on the Application and Improvement of Automatic Test Paper Generation Based on Genetic Algorithm
LUO Yu,LUO Man,XIA De-qi
(China Meteorological Training Center Hunan Branch,Changsha 410125)
In order to solve the problems of slow evolution and premature convergence in standard genetic algorithm,presents an improved genetic al⁃gorithm based on multi-objective optimization model through modified gene coding,population initialization and genetic operators.The ex⁃perimental results indicate that the improved genetic algorithm can achieve better synthesized execution speed,as well as promotes better max fitness(0.79 to 0.84)and average fitness(0.74 to 0.83)of test papers than standard genetic algorithm.
自动组卷;遗传算法;多目标优化;自适应
湖南省气象局重点科研课题(No.XQKJ15A006)、中国气象局气象干部培训学院科研项目(内2014-012)
1007-1423(2017)29-0020-04
10.3969/j.issn.1007-1423.2017.29.005

