基于TDOA的改进定位算法及精度分析
唐发燕,王运锋
(四川大学国家空管自动化系统技术重点实验室,成都610065)
基于TDOA的改进定位算法及精度分析
唐发燕,王运锋
(四川大学国家空管自动化系统技术重点实验室,成都610065)
在无源定位领域中,传统的协同时差(TDOA)定位方法在处理批量目标时,由于计算复杂度高导致定位实时性低和定位精度低。提出一种改进的TDOA算法,通过动态地修正加权最小二乘法(WLS)的加权矩阵,使初值估计与迭代交替进行,达到降低计算复杂度和提高目标位置精度的目的。为了进一步分析定位精度,论述一种定位精度分析方法。实验结果表明改进定位算法既提高原始方法的定位实时性又提高定位精度,另外选择合适的布站形式可以提高定位精度。
0 引言
近年来,由于无源定位具有探测范围大、定位精度高、隐蔽性强、灵活度高等优点,所以在空中交通管理和军事目标定位中运用很多。TDOA(Time Difference Of Arrival)定位是利用多个测量站接收辐射源信号的时间差来对辐射源进行定位[1]。
在无源时差协同定位技术中,应用较广泛地有频差和时差协同定位技术、卡尔曼滤波和时差协同定位技术、Chan与Taylor的时差协同定位技术[2]等。虽然方法较多,但是,当工程实际应用需要处理批量目标时,由于每个目标本应该进行初值估计和迭代修正,但原始方法计算量大会引起部分目标只做初值估计不迭代修正,甚至不处理的情况,这导致了整体目标定位精度低和定位实时性低的问题。为了解决这两个问题,借鉴了目前使用最广泛且较新的基于TWLS的Chan和Taylor的定位方法[2-8],该方法主要思想是每次定位时先利用Chan算法对目标信号进行两次WLS粗定位,粗定位值带入Taylor级数展开算法当中迭代出较精确的目标位置。
两次WLS计算和迭代计算消耗时间太多。本文在原始定位技术上做了一定的改进,改进方法从降低定位算法的计算复杂度和减少定位过程计算量方面同时考虑。首先根据TDOA测量噪声协构造初始加权矩阵,再应用WLS算法计算目标初值。然后根据目标初值更新加权矩阵,利用WLS算法迭代出修正的目标位置。最后,在一定的迭代门限情况下,当修正的目标位置误差达到设置的误差门限时迭代结束。本文将原始协同定位的Chan和Taylor算法分步思想改成通过动态地修正WLS的加权矩阵来让初值估计与迭代同时进行相互交替使用,并且满足条件的定位结果用来计算下次的加权矩阵,从而不必每次都计算初值,比原始方法既要计算初值又要迭代的计算复杂度低。本文通过定位仿真实验比较了原始定位技术与改进定位技术在不同误差范围内的定位精度和不同目标数量的处理时间,通过定位精度仿真实验,分析了对比算法和改进算法在两种不同的布站形式[12]下的定位精度。
1 时差定位算法
1.1 时差定位原理描述
在空间坐标下,辐射源到达两个不同测量站的时间差确定了一对以两基站为焦点的双曲面,多个双曲面将产生交点,这个交点就是辐射源目标的位置[8]。假设时差定位系统一共由N+1个测量站组成,由1个主测量站S0和N个辅测量站Sn组成,它们的真实坐标分别为(xi,yi,zi)T,i=0,1,...,N,辐射源目标T真实坐标为(x,y,z),假设它们的位置分布如图1所示。
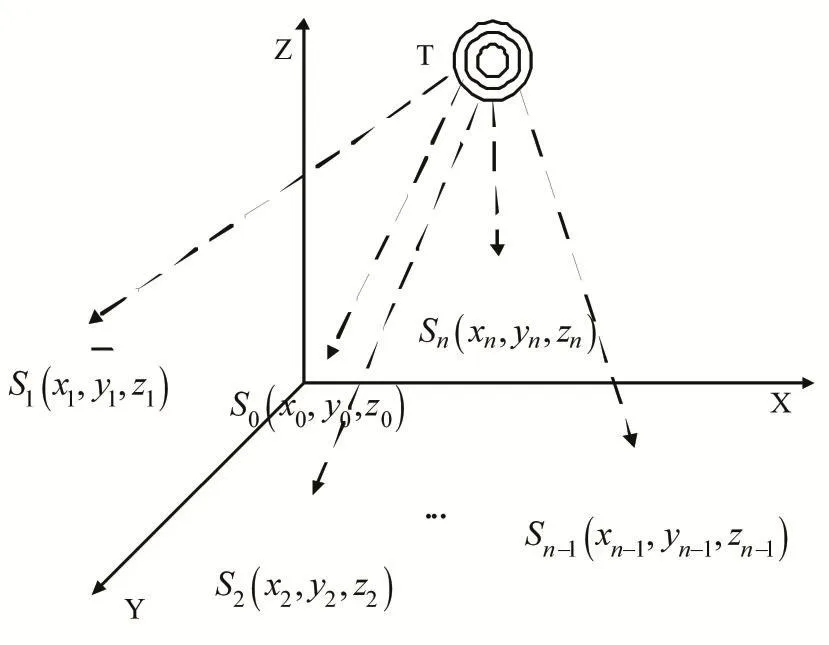
图1 测量站位置分布图
根据图1,得到目标到主站距离r0和到辅测量站距离ri方程为:

其中ri0表示目标到第i个测量的距离与目标到主站距离的距离差值,由TDOA测量值得到。当测量站数目不少于3个时,解(2)式方程组可得到目标的空间位置。
1.2 改进的定位算法
根据上述的距离差方程,需要求解目标位置。将(2)式等式右边展开,然后化简为以(x,y,z,r0)为未知数的方程,得到如下公式:
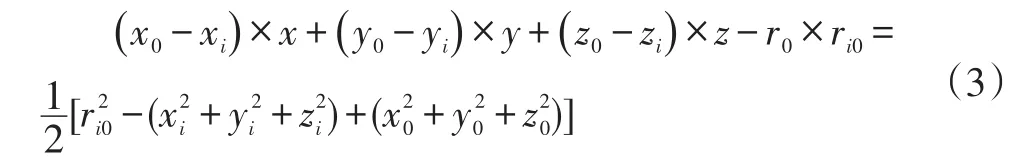
将(3)式化成矩阵形式,令目标za=[x ,y,z,r0]T,那么具有TDOA测量噪声的测量方程为:

Ψ为误差矢量矩阵,xi,yi,zi表示i测量站位置坐标。Ψ可以表示为:

求解(4)非线性方程组时,假设za的元素x,y,z和r0之间相互独立,通过WLS算法进行第一次求解为:

该式是式(4)的WLS解,由于Ψ中的B含有目标与各测量站之间的距离ri0,ri0开始是未知的,所以式(6)不能解出,本文给出改进的定位算法流程如图2所示。

图2 改进定位方法流程图
在图2中,具体算法流程描述如下:
(1)根据测量站位置和TDOA测量值创建矩阵G和H,同时设置计算次数k=0;
(2)计算初始加权误差矩阵Ψ,最开始B矩阵中包含了目标到各个测量站的距离,所以B矩阵未知,因此用TDOA测量噪声的协方差矩阵Q代替加权矩阵Ψ,即Ψ=Q;
(4)计算 za0到每个测量站的距离,形成矩阵
(5)将B带入公式Ψ=BQBT,更新加权矩阵Ψ;
(6)将G、H和更新后的Ψ再带入式(6)可得第一次修正值
(7)计算||za1-za0||,若它小于误差门限ε,则输出最终定位结果,否则设置k=k+1,重复执行步骤(4)(5)(6),直到||za1-za0||小于误差门限或者k大于迭代门限时迭代结束。
当下一个时刻定位时,定位过程改为直接利用上一个时刻定位结果,根据上一时刻目标位置到各个站的距离重新计算加权矩阵,再用WLS方法的计算结果作为当前时刻的目标位置。
2 定位精度方法描述
为了进一步比较原始对比算法和改进算法在定位精度上的差别,下面将描述一种常规定位精度分析方法。定位精度一般用GDOP来衡量,GDOP用来描述定位误差在三维空间中的几何分布。三维平面内的GDOP的方程式为:


式中:
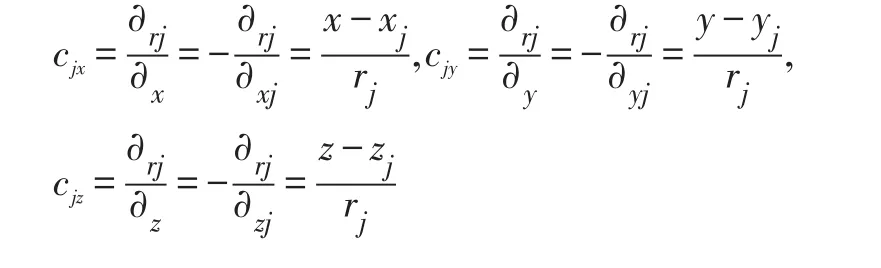
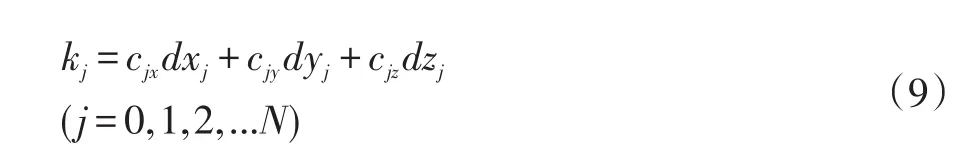
为了求解dx,dy,dz,将(12)式转换为矩阵形式表示为:

dR表示TDOA系统测量误差;dS表示各站站址误差;dX为目标在x,y,z方向上的定位误差。用WLS法可解出定位误差值为:

由于每个时差测量误差中都有主站的测量误差,但站与站之间距离误差是固定的,所以测量误差之间是相关的,站址误差不相关,设测量误差为零均值误差,站址误差方差均相同,那么定位误差协方差矩阵如下:
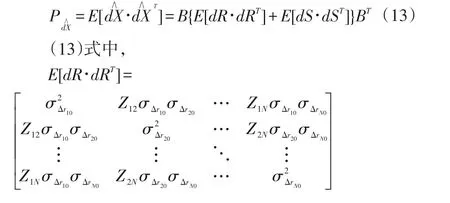

式(20)可求出GDOP值。很明显,降低TDOA测量误差标准差、站址误差标准差可以减小GDOP值,提高定位精度。
3 仿真及分析
设置五个测量站进行仿真实验,表1表示两种场景编号下各个测量站的布站形状以及坐标。实验中均设置电磁波传播速度为3×108m/s。下面将分别对时差定位仿真结果和定位精度仿真结果进行描述和分析。
3.1 时差定位仿真及分析
选择表1中场景编号为1的应用场景,各个测量站坐标如表所示。图3表示提出的改进定位算法和基于Chan与Taylor定位方法同时处理25个目标,但在不同测量误差下多目标的均方根误差(RMSE)比较。图4表示改进方法和Chan与Taylor定位方法在相同周期内处理不同目标数量时所用平均处理时间的比较。

图3 不同定位误差的RMSE比较
从图3可以看出,随着测量误差的增大,原始对比定位方法和本文提出的改进定位方法的RMSE值都增大,但在定位误差较大时,改进方法(黑色线)比原始方法(蓝色线)的RMSE低。分析图4可得出,当目标数量越来越多时,两种方法所需处理时间都越多,但在目标数量较多时,改进方法(黑色线)要比对比原始方法(红色线)所用处理时间少。

图4 不同目标数量时所用的处理时间比较
3.2 定位精度仿真及分析
为了进一步分析原始对比方法和改进方法的定位精度差别,根据第2节描述的定位精度分析方法,仿真了两种不同布站形式下的GDOP图。假设目标高度为10km,目标在二维平面内受控范围为(-200km,200km),设所有场景的测量误差相关系数为0.5,GDOP等高线单位为km。表1表示了在两种布站场景下个测量站的坐标。
选择表1中场景1和2分别做了仿真实验,并假设站址误差方差都为1m,测量误差方差都为25m。最后仿真得到星型布站下Chan和Taylor原始对比方法的GDOP图5和改进方法的GDOP图6,伞型布站下对比方法的GDOP图7和改进方法的GDOP图8。
分析星型布站仿真图5和6得出,目标距离测量站越近,对比方法和改进方法的GDOP值都越低,但是在同一条等高线上,改进方法的GDOP值比对比方法的GDOP值低,说明改进方法的定位精度比原始对比方法的定位精度高。
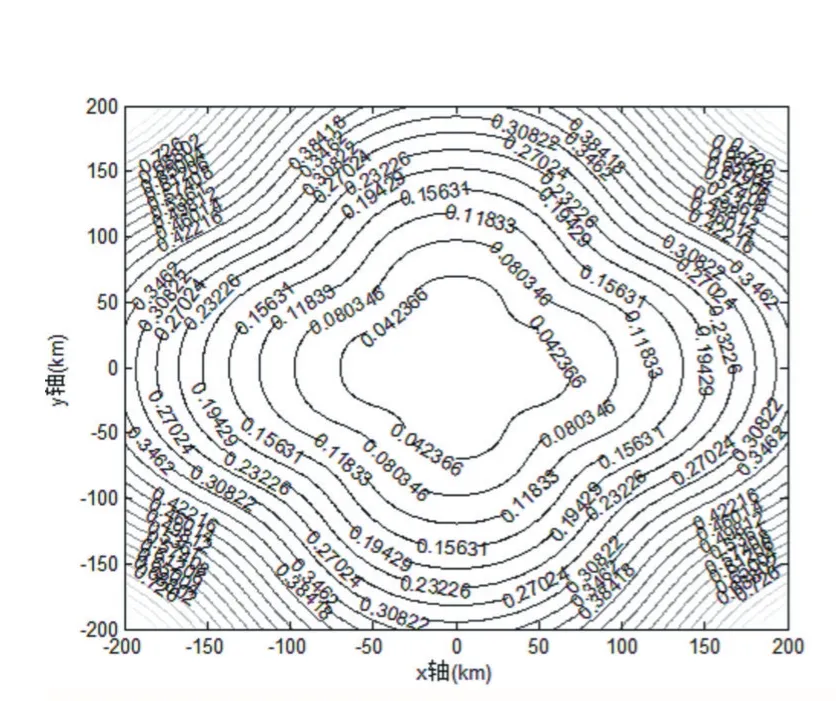
图5 星型布站下Chan和Taylor方法GDOP图

图6 星型布站下改进方法GDOP图

图7 伞型布站下Chan和Taylor方法GDOP图
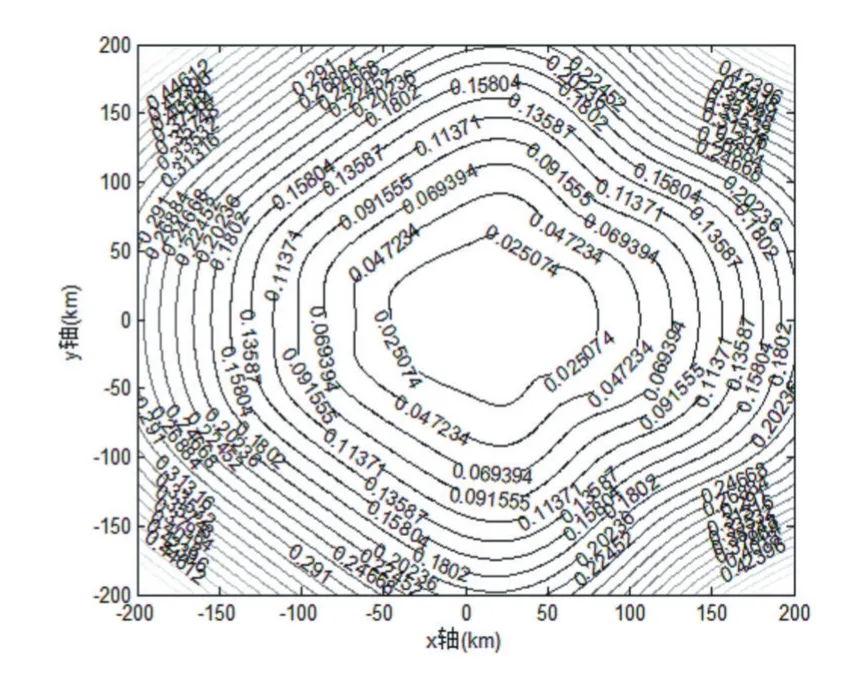
图8 伞型布站下改进方法GDOP图

表1 两种布站场景下各测量站坐标(单位:km)
同样分析伞型布站仿真图7和8得出,目标距离测量站越近,两种方法的GDOP值都越低,但是在同一条等高线上,改进方法的GDOP值比原始对比方法的GDOP值低,说明改进方法的定位精度比原始对比方法的定位精度高。
分析图5和图7得出,在同一等高线上星型布站比伞型布站的GDOP值大,即定位精度要差,所以伞型布站为这两种布站方式当中的较优布站方式。
4 结语
定位仿真实验表明,改进的定位技术在处理目标数量较多时,在相同时差测量误差下,比原始对比方法的定位精度高,并且改进定位技术的处理时间比原始对比协同定位方法所用时间少。另外定位精度仿真实验进一步表明,不管是星型布站还是伞型布站,改进方法都比原始对比方法定位精度高。因此本文的改进方法达到了提高定位精度和提高定位实时性的目的,同时选择伞型布站可以提高定位精度。
[1]张政超,童力.四站时差无源定位精度分析[J].中国电子科学研究院学报,2010,05(582).
[2]Tian Y,Qi B,Zhuo R,et al.Locating Partial Discharge Source Occurring on Transformer Bushing by Using the Improved TDOA Method[C].Condition Monitoring and Diagnosis(CMD),2016 International Conference on.IEEE,2016
[3]闫雷兵,陆音,张业荣.基于改进最小二乘算法的TDOA/AOA定位方法[J].电波科学学报,2016,31(2).
[4]张怡,席彦彪,李刚伟,等.基于卡尔曼滤波的TDOA/AOA混合定位算法[J].计算机工程与应用,2015,51(62).
[5]Li H,Oussalah M.Combination of Taylor and Chan Method in Mobile Positioning[C].IEEE,International Conference on Cybernetic Intelligent Systems.IEEE,2011.
[6]陈德章,唐皓,吴季达.基于Chan和Taylor的TDOA协同定位算法研究[J].计算机科学,2011.
[7]Yang L,Ho K C.An Approximately Efficient TDOA Localization Algorithm in Closed-Form for Locating Multiple Disjoint Sources with Erroneous Sensor Positions[J].IEEE Transactions on Signal Processing,2009,57(12).
[8]李招华,汪毓铎,邵青.基于Chan的TDOA三维定位算法[J].现代电信科技,2014,11(36).
[9]Ren J,Chen J,Bai W.A New Localization Algorithm Based on Taylor Series Expansion for NLOS Environment[J].Cybernetics&Information Technologies,2016,16(5).
[10]江翔.无源时差定位技术及应用研究[D].电子科技大学,2008.
[11]Makki A,Siddig A,Saad M,et al.Indoor Localization Using 802.11 Time Differences of Arrival[J].IEEE Transactions on Instrumenta tion and Measurement,2016,65(614).
[12]吴珂,王俊峰,罗琴.中国空域国内航班飞行拓扑分析[J].四川大学学报(自然科学版),2016,53(75).
唐发燕(1992-),女,重庆人,硕士生,研究方向为雷达数据处理
王运锋(1975-),男,教授,硕士生导师,研究方向雷达数据处理、多源信息融合、航空电子技术
2017-08-18
2017-10-12
TDOA Co-Location;Batch Targets;Real-Time Location;Positioning Accuracy
Improved Location Algorithm and Precision Analysis Based on TDOA
TA Fa-yan,WANG Yun-feng
(Key Laboratory of National ATC Automation System,Sichuan University,Sichuan610065)
In passive location,when traditional TDOA co-location methods'processed batch targets,the large calculation resulted in low real-time lo⁃cation and low positioning accuracy.Presents an improved TDOA algorithm,through correcting the weighted matrix of WLS dynamically to make preliminary value estimation and iterative alternate,so as to achieve the purpose of correcting target location and reduce the amount of calculation.In order to analyze the positioning accuracy further,discusses a location precision method.The experimental results shows that improved location method not only improves old method's real-time location but also enhances positioning accuracy,and chooses suit⁃able base-station layout can increase positioning accuracy.
协同TDOA定位;批量目标;定位实时性;定位精度
国家自然科学基金(No.91338107)
1007-1423(2017)29-0003-07
10.3969/j.issn.1007-1423.2017.29.001

